 |
Главная |
Анализ частей конструктивной системы
|
из
5.00
|
(1) Действует 2.4.2 (1).
(2) Реакции опор, внутренние силы и моменты на краях части конструктивной системы могут быть приняты из анализа конструкций при нормальной температуре, как указано в 2.4.2.
(3) Деление конструктивной системы на части производится на основании анализа возможных температурных расширений и деформаций, таким образом, чтобы их взаимодействие можно было оценить при помощи независимых от времени граничных условий и схемы опирания в течение всей продолжительности пожара.
(4)Р Расчет части анализируемой при пожаре конструктивной системы должен включать обоснование принятой схемы разрушения, характеристик материалов в зависимости от температуры их нагрева, жесткости конструкции, результатов температурных расширений и деформаций (непрямые воздействия пожара).
(5) Граничные условия на опорах, силы и моменты на краях части конструктивной системы, принятые в момент времени t = 0, при пожаре считаются неизменными.
Общий анализ конструктивной системы
(1)Р Общий анализ конструктивной системы при пожаре должен включать обоснование принятой схемы разрушения, характеристики материалов в зависимости от температуры их нагрева, жесткости конструкций, результатов температурных расширений и деформаций (непрямые воздействия пожара).
Характеристики материалов
Общие положения
(1)Р Приведенные в настоящем разделе значения характеристик материалов являются их нормативными значениями (см. 2.3 (1)Р).
(2) Данные значения используются в упрощенных (см. 4.2) и общих (см. 4.3) методах расчета.
Могут быть использованы другие законы изменения характеристик материалов, если они не противоречат экспериментальным данным.
Примечание — Характеристики легкого бетона в EN 1992-1-2 не рассмотрены.
(3)Р Механические характеристики бетона, напрягаемой и ненапрягаемой арматуры при нормальной температуре (20 °С) принимаются по EN 1992-1-1.
Прочностные и деформационные характеристики материалов при повышенных температурах
Общие положения
(1)Р Приведенные прочностные и деформационные характеристики определены экспериментально без рассмотрения ползучести при режимах нагрева от 2 до 50 К ∙ мин–1. Для других режимов нагрева достоверность прочностных и деформационных характеристик должна быть явной.
Бетон
Сжатый бетон
(1)Р Прочностные и деформационные характеристики одноосно напряженного состояния бетона при повышенных температурах принимаются по диаграмме деформирования, приведенной на рисунке 3.1.
(2) Диаграмма деформирования (см. рисунок 3.1) определяется двумя параметрами:
— сопротивление сжатию fc,q;
— относительная деформация ec1,q, соответствующая fc,q.
(3) Значения указанных в 3.2.2.1 (2) параметров приведены в таблице 3.1 в зависимости от температуры бетона. Для промежуточных значений температуры допускается линейная интерполяция.
(4) Указанные в таблице 3.1 значения применимы для бетона нормальной плотности с силикатным
и карбонатным (содержащим не менее 80 % от массы карбонатной составляющей) заполнителями.
(5) Значения ecu1,q, определяющие ниспадающую ветвь диаграммы, принимаются по таблице 3.1: для бетона с силикатным заполнителем — по данным графы 4, с карбонатным заполнителем — по данным графы 7.
(6) Для тепловых воздействий (раздел 3 EN 1991-1-2), имитирующих реальный пожар, математическую модель диаграммы деформирования бетона (см. рисунок 3.1) следует модифицировать, особенно для ниспадающей ветви.
Таблица 3.1 — Значения основных параметров диаграммы деформирования сжатого бетона
при повышенных температурах
| Температура бетона q,°C | Силикатный заполнитель | Карбонатный заполнитель | ||||
| fc,q/fck | ec1,q | ecu1,q | fc,q/fck | ec1,q | ecu1,q | |
| 0,0025 | 0,02 | 0,0025 | 0,02 | |||
| 0,004 | 0,0225 | 0,004 | 0,0225 | |||
| 0,95 | 0,0055 | 0,025 | 0,97 | 0,0055 | 0,025 | |
| 0,85 | 0,007 | 0,0275 | 0,91 | 0,007 | 0,0275 | |
| 0,75 | 0,01 | 0,03 | 0,85 | 0,01 | 0,03 | |
| 0,6 | 0,015 | 0,0325 | 0,74 | 0,015 | 0,0325 | |
| 0,45 | 0,025 | 0,035 | 0,6 | 0,025 | 0,035 | |
| 0,3 | 0,025 | 0,0375 | 0,43 | 0,025 | 0,0375 | |
| 0,15 | 0,025 | 0,04 | 0,27 | 0,025 | 0,04 | |
| 0,08 | 0,025 | 0,0425 | 0,15 | 0,025 | 0,0425 | |
| 0,04 | 0,025 | 0,045 | 0,06 | 0,025 | 0,045 | |
| 0,01 | 0,025 | 0,0475 | 0,02 | 0,025 | 0,0475 | |
| — | — | — | — |
(7) Возможное увеличение сопротивления бетона в фазе охлаждения в расчетах не учитывается.

| Диапазон | Напряжение s(q) |
| e £ eс1,q | 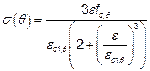
|
| eс1,q < e £ ecu1,q | Для численных расчетов следует принимать ниспадающую ветвь. Допускаются линейные и нелинейные модели |
Рисунок 3.1 — Математическая модель диаграммы деформирования сжатого бетона
|
из
5.00
|
Обсуждение в статье: Анализ частей конструктивной системы |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

