 |
Главная |
АДДИТИВНЫЕ СИСТЕМЫ СОГЛАСОВАНИЯ
|
из
5.00
|
Аддитивные системы согласования и координации параметров используют различные ряды чисел, образованные путем сложения. Рассмотрим некоторые примеры аддитивных систем согласования.
Ряд золотого сечения (золотой ряд) последовательная система чисел, подчиняющихся закону:

Отрезки золотого сечения составляют: больший — 0,618 целого, меньший — 0,382 целого.
Гармоническое деление отрезка золотым сечением было известно еще в глубокой древности (хотя сам термин введен Леонардо да Винчи), и не исключено, что ряд золотого сечения можно назвать первым, придуманным человеком для согласования параметров. Впрочем, не придуманным, а просто позаимствованным у Её Величества Природы! Золотому ряду подчиняется членение веток и листьев деревьев, расстояния между витками ракушек, размеры человеческого тела — любая динамика роста в Природе хорошо отражается закономерностями золотого ряда. Везде, где человек ощущает гармонию — в звуках, в растениях, в размерах прекраснейших сооружений древности и современной архитектуры, — везде присутствует золотое сечение.
Кстати, и в пятиконечной звезде отношение всех отрезков подчинено золотому сечению.
Есть и такая интересная мысль: если для мужчин рост делится на две части (часть А — от пупка вниз до пяток, часть Б—от пупка вверх до темечка) по закону золотого сечения: А»1,65—1,70, то у бедных, обиженных при сотворении мира женщин часть А около 1,5. Чтобы приблизиться к богом данной стройности мужчин (где вы видели у нас стройных мужичин?) женщины придумали высокие каблуки, удлиняющие часть А.
Числа Фибоначчи, итальянского математика, жившего в 1180 — 1240 гг. — ряд чисел, подчиняющихся следующей закономерности 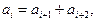 т. е. каждое число этого ряда равно сумме двух предыдущих чисел. Значение
т. е. каждое число этого ряда равно сумме двух предыдущих чисел. Значение  . Цельночисловой ряд Фибоначчи — 1; 2; 3: 5; 8; 13; 21; 34; 55; 89; 144 и т. д. Числа этого ряда сначала растут очень медленно, но затем их рост становится стремительным. Для i=20
. Цельночисловой ряд Фибоначчи — 1; 2; 3: 5; 8; 13; 21; 34; 55; 89; 144 и т. д. Числа этого ряда сначала растут очень медленно, но затем их рост становится стремительным. Для i=20  >10000. Большинство членов этого ряда не кратны друг другу, что, безусловно, надо рассматривать как сдерживающий фактор, затрудняющий применение этого ряда для целей согласования параметров.
>10000. Большинство членов этого ряда не кратны друг другу, что, безусловно, надо рассматривать как сдерживающий фактор, затрудняющий применение этого ряда для целей согласования параметров.
Члены ряда Фибоначчи близки к пропорциям золотого сечения, причем чем больше номера членов ряда, тем точнее выполняется «золотое» соотношение.
Числа Фибоначчи — тоже из Природы, ими описываются многие биологические процессы (например, так размножаются кролики) или даже из ближнего Космоса — им подчинены взаимные расстояния планет, основные их размеры, периоды обращения.
Модульные системы. В простейшем виде проектный линейный модуль M выступает как разность арифметической прогрессии, образуемой рядом чисел а1, а2,...,аi,...,ат.. Любой член этого ряда может быть получен по известной формуле
 .
.
Система предпочтительных чисел. Аддитивный ряд предпочтительных чисел (АРПЧ) сочетает преимущества (для стандартизации сборных конструкций) модульной системы, построенной на кратности величин, с золотым рядом, в котором используется то его свойство, когда каждый член ряда, начиная с третьего, может представлен в виде суммы некоторого количества первых а1 вторых а2 членов. Величины а1 и а2 должны быть связаны по закону золотого сечения.
| 2´70 | |
| 70+110 | |
| 3´70 | |
| 2´110 | |
| 2´70+110 | |
| 4´70 | |
| 70+2´110 | |
| 3´70+110 | |
| 3´110 | |
| 5´70 | |
| 2´70+2´110 | |
| 4´70+110 | |
| 70+3´110 | |
| 6´70 | |
| 3´70+2´110 | |
| 4´110 | |
| 5´70+110 | |
| 2´70+3´110 | |
| 70´70 | |
| 4´70+2´110 | |
| и т.д. |
Таким образом, на базе всего двух модулей (понимая под а1=М1 и а2=М2), из которых один может быть выбран произвольно, т.е. исходя из функциональных и конструктивно-технологических требований, а второй определяется как последовательный член золотого ряда, возможно составление ряда предпочтительных чисел являющегося основой для координации и согласования параметров.
Ряд исследователей доказывает целесообразность перехода на такую систему взаимосвязанных двух модулей в строительстве жилых зданий, подчеркивая необходимость последовательного применения системы для определения величин, начиная с оборудования и мебели и кончая домом и жилым комплексом. В качестве примера рассматривается АРПЧ при M1=70 и M2=110.
Заметим, что выделенные члены ряда 70; 110; 180; 290; 470 и далее подчиняются закону образования чисел Фибоначчи и — с небольшими округлениями — являются членами золотого ряда:  и т.д.
и т.д.
Промежуточные числа получены суммированием некоторого количества основных двух модулей. Модулор (иногда — модулер или модулёр) — ряд чисел, построенный по закону золотого сечения и одновременно отражающий пропорции человеческой фигуры. Автор модулора, всемирно известный французский архитектор и теоретик архитектуры Ле Корбюзье Шарль Эдуард (1887-1965), начал работать над своей шкалой размеров в 1909-1910 гг, будучи еще мало известным художником-самоучкой Шарлем Жаннере.
К середине 40-х годов окончательно сформировалась система пропорциональных величин, появилось само название «Модулор» и широко теперь известная эмблема—стилизованное изображение мужской фигуры с поднятой рукой и двумя шкалами размеров — «красный» ряд и «синий» ряд. Величины второго ряда равны удвоенным величинам первого:
«Красный» ряд 6 10 16 27 43 70 113 183
«Синий» ряд 8 13 20 33 53 86 140 226.
(При условном росте человека, равном 6 футам. Первоначально рост был принят равным 175 см и затем увеличен, чтобы иметь возможность получить ряды модулора как в сантиметрах, так и в дюймах.
Укажем на интересное совпадение: японские зодчие издавна применяли «токийский» модуль, равный 182 см.
Интересно отметить, что модулор может быть отнесен и к рядам мультипликативным, со знаменателем прогрессии (q=1,62 (см. ниже).)
Сам Ле Корбюзье рассматривает модулор, как «... рабочий инструмент, целый диапазон числовых размеров, которыми можно пользоваться для проектирования... изделий массового промышленного производства, а также для обеспечения единства крупных архитектурных композиций» и считал, что этот инструмент должен лежать на чертежном столе рядом с карандашом, рейсшиной и угольником. Теперь архитектор сказал бы, что «этот инструмент должен быть введен в базу данных ЭВМ».
Альберт Энштейн в переписке с Ле Корбюзье так отзывается о модулоре: «Это гамма пропорций, которая делает плохое трудным и хорошее легко достижимым».
|
из
5.00
|
Обсуждение в статье: АДДИТИВНЫЕ СИСТЕМЫ СОГЛАСОВАНИЯ |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

