МУЛЬТИПЛИКАТИВНЫЕ СИСТЕМЫ СОГЛАСОВАНИЯ

Под мультипликативными системами согласования и координации параметров понимают системы, в которых размеры и параметры укладываются в ряды чисел, кратных постоянному множителю.

Такие системы основаны на использовании геометрических прогрессий, в которых любой (i-й) член ряда определяется по формуле а_i =q^i-1a₁, где q- знаменатель прогрессии, a₁ — первый член ряда.

Поиск наиболее рациональных рядов чисел как базы для построения параметрических или размерных радов на основе геометрических прогрессий давно ведется. Так, в начале I века до н. э. на римских водопроводах использовались колеса, диаметр которых изменялись по закону геометрической прогрессии. В конце XVII — начале XVIII веков геометрическая прогрессия была применена в музыке: октава (октава — интервал между частотами двух тонов, образующих отношение 2:1) была разделена на 12 интервалов со знаменателем прогрессии .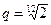

Академик А. В. Гадалин разработал еще в конце прошлого столетия теорию проектирования металлорежущих станков и обосновал целесообразность выбора их параметров, в частности, чисел оборотов по ряду геометрической прогрессии. Развили это направление немецкий инженер Г. Шлизингер, академик В. И. Дикушин и др.

Ряды, построенные по закону геометрической прогрессии, обладают постоянством относительной разницы между любыми смежными членами ряда, в отличие от рядов, основанных на арифметической прогрессии, где относительная разница между низшими членами ряда значительно превышает разницу между высшими.

Ряды предпочтительных чисел (РПЧ, как они наиболее часто называются, или МРПЧ — мультипликативные РПЧ, как их назовем мы, чтобы отличить от описанных выше аддитивных РПЧ) известны сейчас уже достаточно широко. О предпочтительных числах и рядах предпочтительных чисел написано множество статей и целые книги.

Введение рядов чисел, основанных на геометрических прогрессиях, которые до настоящего времени и принято было называть предпочтительными, связано с именем французского инженера Ш. Ренара, применившего их в 80-х годах прошлого столетия для установления диаметров канатов аэростатов.

После длительного периода забвения числа Ш. Ренара в двадцатых-тридцатых годах нашего столетия стали проникать в технику.

В 1953 г. Международная организация по стандартизации (ИСО) приняла рекомендацию и установила международную систему предпочтительных чисел.

По рекомендации ИСО многие страны приняли свои национальные стандарты на ряды предпочтительных чисел. В СССР был утвержден ГОСТ 8032-56, установивший «...предпочтительные числа и их ряды, которые должны быть положены в основу выбора градаций параметров и размеров, а также отдельных характеристик продукции, выпускаемой всеми отраслями народного хозяйства».

РПЧ представляет собой десятичные ряды геометрической прогрессии вида , где N=5; 10; 20; 40; 80 - номер ряда.

Основные ряды предпочтительных чисел приведены в табл. 1. Они могут быть бесконечно продолжены умножением табличных значений на величину 10k, где k—целое положительное или отрицательное число.

Кроме «чистых» основных рядов в технике находят применение производные ряды предпочтительных чисел, образованные путем отбора каждого n-го члена основного ряда. Например, производный ряд R 20/3 получен путем отбора каждого третьего члена R 20.

Свойства РПЧ таковы, что если при выборе мощности, грузоподъемности, размеров, давлений и пр. придерживаться определенного обоснованного ряда предпочтительных чисел, то этим обеспечивается согласование параметров и размеров каждого отдельного изделия (или группы изделий) со всеми связанными с ним видами продукции.

Действительно, произведения или частные предпочтительных чисел сами являются членами РПЧ. Целые положительные или отрицательные степени любого предпочтительного числа — члены ряда.

Начиная с R 10 в числах рядов находится число 3,15@p, поэтому выбирая в РПЧ радиусы или диаметры, автоматически в рядах получают длины окружностей, площади кругов, окружные скорости и т. д. Ряды предпочтительных чисел не свободны от недостатков. По вопросу преимуществ и недостатков РПЧ в 1968-1969 гг. на страницах журнала «Стандарты и качество» развернулась довольно бурная дискуссия.

Во-первых, РПЧ — иррациональные числа, определяемые с той или иной степенью округления. Во-вторых, сумма предпочтительных чисел не обязательно есть число из РПЧ. То же наблюдается при умножении предпочтитель­ного числа на постоянный множитель не из ряда.

При постоянстве относительной разницы между смежными членами РПЧ (прямо противоположно арифметическим рядам) не имеют постоянства абсолютной разницы.

По-видимому, необходимо обратить внимание и на своеобразный психологический барьер на пути внедрения предпочтительных чисел: эти числа «непривычны», они «не круглые». Конечно, каждый волен любить или не любить те или иные числа, одним нравится число 13, другой панически избегает его и т. д., однако в технике должно отдавать предпочтение более серьезным мотивам. Барьер этот постепенно преодолевается, и сейчас имеется очень много примеров активного внедрения системы МРПЧ (РПЧ по ИСО) в машиностроении, на транспорте и т. д.