Расчёт коротких трубопроводов

РАСЧЁТ ТРУБОПРОВОДОВ

 

 

МЕТОДИЧЕСКИЕ УКАЗАНИЯ

 

к расчётной работе по дисциплине «Гидрогазодинамика»

 

Составитель А.В. Севостьянов

 

 

Липецк

Липецкий государственный технический университет

УДК 621.6 (07)

С 281

 

Рецензент Е.М. Крамченков

 

Севостьянов, А.В.

С 281 Расчёт трубопроводов [Текст]: методические указания к расчётной работе по дисциплине «Гидрогазодинамика» / А.В. Севостьянов. – Липецк: Изд-во ЛГТУ, 2014. – 47 с.

В методических указаниях приводится алгоритм расчёта коротких и длинных трубопроводов, описан подбор насоса для выбранных рабочих параметров длинного трубопровода.

Методические указания предназначены для студентов I курса специальности «Промышленная теплоэнергетика».

Табл. 3. Ил. 28. Библиогр.: 3 назв.

 

 

© ФГБОУ ВПО «Липецкий государственный технический университет», 2014

 

Оглавление

Введение. 6

1. Расчёт коротких трубопроводов. 8

2. Расчёт длинных трубопроводов. 10

3. Построение графика пьезометрической линии. 12

4. Подбор насоса для сети. 13

5. Задания. 14

5.1. Варианты задания на расчёт короткого трубопровода. 15

5.2. Варианты задания на расчёт короткого трубопровода. 34

6. Пример решения – расчёт короткого трубопровода. 35

6.1. Введение. 35

6.2. Определение объёмного расхода. 36

6.3. Определение показания манометра 38

6.4. Определение напора насоса. 40

7. Пример решения – расчёт длинного трубопровода. 41

7.1. Расчёт магистрали. 41

7.2. Расчёт ответвления. 43

7.3. Построение графика пьезометрической линии. 45

7.4. Подбор насоса. 46

Библиографический список. 47

Приложение. 47

 

 

 

Перечень условных обозначений

d – диаметр трубопровода, м;

d_н – наружный диаметр трубопровода, м;

g = 9,81 м/с² - ускорение силы тяжести;

h – высота жидкости в колене жидкостного манометра, м;

h_вс – высота всасывания насоса, м;

h_1-2 – потери напора между сечениями 1 и 2, м;

h_w – потери напора на вязкое трение, м;

h_м.с. – потери напора на местном сопротивлении, м;

l – длина трубопровода, м;

р – давление, Па;

р₀ – давление на поверхности жидкости, Па;

s – толщина стенки трубы, м;

t – температура, °С;

w – скорость, м/с;

z – геометрическая высота, м;

D_у – условный диаметр трубопровода, м;

D_к – диаметр рабочего колеса насоса, м;

H – высота, пьезометрический напор, м;

H_н – напор насоса, м;

H_c – характеристика сети, м;

H_cт – статический напор, м;

K - сопротивление трубопровода, с²/м⁵;

Re – критерий Рейнольдса;

– объёмный расход, м³/с;

- потребный расход, м³/с;

S – площадь, м²;

- коэффициент местного сопротивления;

- коэффициент местного сопротивления поворота;

- коэффициент трения;

- коэффициент кинематической вязкости, м²/с;

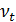- коэффициент кинематической вязкости для заданной температуры, м²/с;

- коэффициент кинематической вязкости для t = 50 °C, м²/с;

π = 3,14159265358;

ρ – плотность, кг/м³;

Δ_э – эквивалентная шероховатость, м;

Δh - удельный перепад напора, м/м;

ΔH - перепад напора, м;

Δz – перепад геометрических высот, м.

Обозначения на схемах

В – вентиль;

Др – дроссель;

М – манометр;

Н – насос;

Ф – фильтр.

Индексы

верхние:

(1) и (2) – первое и второе приближения;

нижние:

ат – атмосферный;

в – вода;

вс – всасывание;

н – насос;

расч – расчётный;

рт – ртуть;

факт – фактический;

экв – эквивалентный;

В – вентиль;

Др – дроссель;

Ф – фильтр.

Введение

Основными результатами расчёта трубопроводов являются сводка диаметров труб на всех участках и потери напора или давления от источника до диктующей точки. Диктующей точкой называется место расположения потребителя, который находится в самом невыгодном положении по сравнению с другими потребителями. Если потребитель в критической точке получает необходимый расход при заданном напоре, то снабжение остальных потребителей не вызывает проблем. Потери напора в сети наряду с потребным расходом являются основными параметрами, определяющими выбор насоса.

Основой гидравлического расчёта трубопроводов является уравнение Бернулли [1]. Для несжимаемой среды уравнение имеет следующий вид

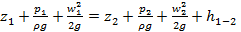. (1)

Важным моментом является выбор положения плоскости сравнения 0-0, от которой производится отсчёт геометрических высот z₁ и z₂ для двух живых сечений, в которых определяются необходимые параметры.

Потери напора h_1-2 между выбранными живыми сечениями являются суперпозицией потерь на вязкое трение в жидкости и потерь на местных сопротивлениях. Потери на вязкое трение определяются по формуле Д’Арси

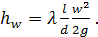(2)

Коэффициент трения в этом соотношении зависит от режима течения и области сопротивления. Режим течения можно установить по значению критерия Рейнольдса. Значение критерия Рейнольдса определяется характерными параметрами: средней по живому сечению скоростью, внутренним диаметром трубы и коэффициентом кинематической вязкости жидкости для заданной температуры

. (3)

Коэффициент кинематической вязкости сильно зависит от температуры. Для воды используется эмпирическая формула

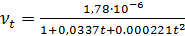. (4)

Для минеральных масел применяется формула

, (5)

для солярового масла ν₅₀=7·10^-6 м²/с, n=1.54.

Если Re < 2300, то течение ламинарное. Для ламинарного течения коэффициент трения определяется по формуле

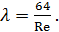(6)

Для турбулентного течения (Re > 2300) выбор формулы для коэффициента трения зависит от области сопротивления. Границы области определяются с помощью комплекса 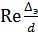. Для области гидравлически гладкой трубы

, (7)

для переходной (доквадратичной) области

(8)

и для области гидравлически шероховатой трубы (квадратичной области)

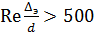. (9)

Для каждой области сопротивления предлагаются свои соотношения для коэффициента трения. Наиболее популярными является степенные формулы:

для гидравлически гладких труб – формула Блазиуса

, (10)

для переходной области – формула Альтшуля

, (11)

для гидравлически шероховатых труб – формула Шифринсона

. (12)

Степенные формулы справедливы в диапазоне значений Re < 10⁵. Для значений Re > 10⁵ формулы (8) – (10) дают заметную ошибку, поэтому в этом диапазоне значений Re используются логарифмические формулы:

для гидравлически гладких труб – формула Конакова

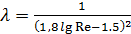, (13)

для гидравлически шероховатых труб – формула Никурадзе

. (14)

Для переходной области применяется формула Коулбрука и Уайта

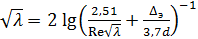. (15)

Уравнение (15) является трансцендентным и по этой причине непопулярным. Таблицы и графики, основанные на этом уравнении, можно найти в справочниках [2].

Потери на местных сопротивлениях определяются по формуле Вейсбаха

. (16)

По умолчанию в уравнение (14) входит скорость за сопротивлением. Коэффициенты местных сопротивлений в диапазоне значений Re > 1000 определяются только формой местного сопротивления и их значения для наиболее часто встречающихся местных сопротивлений приводятся в справочниках [2].

Для несжимаемых жидкостей одним из параметров потока является объёмный расход

, (17)

для потока в круглой цилиндрической трубе

. (18)

Расчёт коротких трубопроводов

Короткими называются трубопроводы, в которых потери напора на вязкое трение и на местных сопротивлениях сопоставимы по величине.

Существует несколько типов задач, встречающихся при расчёте коротких трубопроводов. Задача в прямой постановке (конструктивный расчёт) предполагает задание потребных расходов и плана трубопровода с геометрическими отметками узловых точек. В этом случае определяются диаметры труб на каждом участке и суммарные потери. Проверочный расчёт предполагает известными диаметры всех участков трубопровода. Целью проверочного расчёта является определение пропускной способности трубопровода, т.е. определение расходов при заданном напоре или определение потребного напора при заданных расходах.

Для определения общих потерь в трубопроводе используется принцип суперпозиции (наложения) потерь

. (19)

Уравнение (17) выписано для трубопровода, содержащего n участков и m местных сопротивлений и справедливо для случаев, когда расстояние между местными сопротивлениями не менее 20 50 калибров (диаметров трубы).

Основным расчетным соотношением для коротких трубопроводов является уравнение Бернулли (1). Для успешного применения уравнения (1) необходимо выполнить следующую последовательность действий:

а) выбрать положение плоскости сравнения. Строгих требований по выбору плоскости сравнения нет, рекомендуется размещать её наиболее удобным для последующего решения образом;

б) выбрать два живых сечения потока. Наиболее удачным считается такое расположение живых сечений, при котором в этих сечениях сосредотачивается большая часть известных параметров и неизвестный параметр. Не всегда удаётся выбрать живые сечения с первого раза, иногда приходится возвращаться к этому пункту и корректировать положение этих сечений;

в) рекомендуется выписать уравнение Бернулли в виде, наиболее удобном для последующего решения. Для несжимаемых жидкостей – это уравнение (1);

г) необходимо идентифицировать параметры уравнения (1) с исходными данными;

д) выписать уравнение Бернулли с максимальным использованием исходных данных;

е) разрешить полученное уравнение относительного неизвестного. Может случиться так, что в полученном уравнении окажутся два или более неизвестных. В этом ситуации необходимо привлекать так называемые замыкающие уравнения. Самым популярным из них является уравнение баланса расходов

, (20)

которое позволяет выразить скорость в одном сечении через скорость в другом.

При решении сложных задач очень полезным может быть приём, называемый декомпозицией, т.е. разложение сложной задачи на последовательность более простых, что сильно облегчает решение поставленной задачи. В таких ситуациях приходится применять уравнение (1) несколько раз.