ВЛИЯНИЕ ТЕМПЕРАТУРЫ НА СКОРОСТЬ ХИМИЧЕСКОЙ РЕАКЦИИ. МЕТОД “УСКОРЕННОГО СТАРЕНИЯ ЛЕКАРСТВЕННОЙ ФОРМЫ”

Температура влияет на скорость химических реакций. Как правило, при повышении температуры скорость химических реакций увеличивается.

Зависимость скорости реакции от температуры приближенно описывается эмпирическим правилом Вант-Гоффа. Оно читается так:

при повышении температуры на 10° скорость реакций увеличивается примерно в 2-4 раза.

- температурный коэффициент скорости реакции, принимающий значения от 2 до 4.

Если же температура возрастает от t₁ до Т₂, то для небольших интервалов температур правило Вант-Гоффа выполняется в виде:

, откуда .

Правило Вант-Гоффа используется в методе “ускоренного старения лекарственной формы”.

Метод позволяет определять:

1. Срок годности (время хранения) лекарственной формы.

2. Условия хранения (температуру, при которой обеспечивается заданный срок годности).

Под сроком годности подразумевают время, в течение которого препарат сохраняет 90% своей фармакологической активности, т.е. время, в течение которого превращению подвергается 10% действующего начала (лекарственного вещества в лекарственной форме). Для некоторых препаратов эта цифра составляет 5%.

Для определения срока годности лекарственного препарата образец препарата выдерживают при повышенной температуре Т₂ по сравнению с температурой хранения t₁. Повышение температуры ускоряет течение процессов, приводящих к потере активности препарата при температуре хранения.

Температура опыта выбирается такой, чтобы она не вызывала дополнительных побочных превращений и была на 10nвыше температуры хранения (n - целое число).

Итак: t₁ -температура хранения лекарственного препарата;

Т₂ - температура опыта.

Т₂ = t₁+10n

Определяют время t₂, в течение которого превращению подвергается 10% действующего начала, что соответствует массе m.. На основании полученной величины рассчитывают скорость превращения лекарственного вещества при температуре Т₂:

(1)

- константа скорости реакции превращения лекарственного вещества при Т₂,

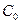- его начальная концентрация.

По этой же закономерности можно было бы рассчитать скорость превращения лекарственного вещества при температуре Т₁

(2)

- константа скорости реакции превращения лекарственного вещества при t₁,

- время хранения (срок годности).

разделив (1) на (2), получаем: , откуда .

Далее для расчета применяется правило Вант-Гоффа: , но Т₂ – t₁ = t₁+ 10n – t₁ = 10n, следовательно, , откуда

Было принято допущение, что γ = 2. Для более точного определения срока годности данным методом необходимо экспериментально определить γ для данного превращения.

Более точную математическую зависимость скорости реакции от температуры устанавливает уравнение Аррениуса. Эмпирическоеуравнение Аррениуса имеет вид:

- константа скорости, Т - температура, А и В - эмпирические константы.

Уравнение показывает линейную зависимость от .. Аррениусом было установлено, что график этой зависимости имеет следующий вид:

 

 

Рис.1.

Для нахождения физического смысла константы А уравнения Аррениуса используют уравнение изобары химической реакции, устанавливающее зависимость константы равновесия обратимой химической реакции от температуры:

- константа равновесия обратимой химической реакции,

- тепловой эффект реакции.

Если принять, что , где - константа скорости прямой реакции, - константа скорости обратной реакции, а величину рассматривать как разность двух энергетических величин и ,т. е. ,то сделав элементарные математические преобразования и приняв некоторые допущения, можно получить:

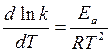- уравнение Аррениуса в дифференциальнойформе.

Дальнейшее математическое преобразование дает уравнение вида:

- аналитическоеуравнение Аррениуса. (см. вывод -учебник В. А.Киреева, §198).

Сопоставляя аналитическое и эмпирическое уравнения Аррениуса, получаем, что эмпирическая

константа 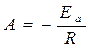. Величина Еа - энергия активации.

Если в аналитическом уравнении Аррениуса константу В заменить на 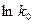, уравнение будет иметь вид: и его можно записать так:

уравнение Аррениуса в экспоненциальнойформе (е - основание натурального логарифма).

- предэкспоненциальный множитель - величина, пропорциональная общему количеству столкновений всех молекул в единице объема за единицу времени.

Аналитическое уравнение Аррениуса в виде обосновывает обратный характер линейной зависимости от (См. рис.1).

Физический смысл энергии активации.

Условием протекания реакции является столкновение молекул, однако еще Аррениус указал, что не каждое столкновение приводит к химическому превращению. Столкновения между части­цами, приводящие к химическому превращению, называют эффективными.Они возможны меж­ду активными молекулами. Активныминазываются молекулы, обладающие в момент столкнове­ния необходимым избытком энергии по сравнению со средней величиной и способные вступать в химическое взаимодействие. Среди молекул при заданных условиях всегда имеются молекулы, обладающие избытком энергии, достаточным для химического взаимодействия - активные моле­кулы.

Число активных молекул N связано с общим числом молекул в системе No соотношением:

В это уравнение также входит величина Еа.Дадим такое определение энергии активации:

Энергия активации - это то избыточное количество энергии (по сравнению со средней величиной), которой должны обладать молекулы в момент столкновения, чтобы быть способными к данному химическому взаимодействию.

Проиллюстрировать понятие энергии активации можно с помощью рисунка 17.8 учебника К.И.Евстратовой...(стр.284-285). Необходимо обратить внимание, на то, что разность средних энергий уровней II и I равна тепловому эффекту реакции.

Из анализа рисунка вытекает определение понятию энергетический барьер- минимальный запас

энергии молекул, при котором происходит химическое взаимодействие.

 

Энергия активации реакции Еа зависит от природы реагирующих веществ и катализатора и не зависит от температуры. Для реакций, протекающих в растворах, энергия активации зависит от природы растворителя.

Скорость реакции зависит от Еа.Чем выше энергия активации, тем при данных условиях меньше активных молекул и ниже скорость реакции.

С повышением температуры быстрее увеличивается скорость той реакции, энергия актива-ции которой выше (обоснование вытекает из анализа уравнения Аррениуса в дифференциальной форме).

В ряде случаев расчет константы скорости по уравнению дает завышенный результат. Чтобы расчетные данные в таких реакциях совпадали с опытными
значениями, в уравнение для расчета константы скорости вводят дополнительный множитель Р,
называемый стерическим фактором.Стерический фактор учитывает пространственную ориентацию молекул в момент столкновения. Уравнение для расчета константы скорости приобретает

вид: -

При неблагоприятной ориентации Р < 1, при благоприятной - Р = 1.

Способы определения энергии активации.

1. Графический:

2. Расчетный, основанный на измерении константы скорости реакции при двух температурах t₁ и Т₂.

(1)

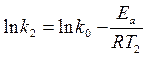(2)

Вычитая из первого уравнения второе, получаем:

, откуда

Определив константу скорости реакции при одной температуре (T₁) и зная энергию активации реакции, можно рассчитать константу скорости реакции при другой температуре (Т₂) по уравнению: