Тема 4.4 Линейная корреляция и коэффициент корреляции

При проведении некоторых химико-аналитических исследований возникает необходимость оценить характер и степень зависимости одной экспериментальной величины от другой или других исследуемых величин. С точки зрения математической статистики решение задач подобного рода направлено на установление корреляции между случайными величинами. Две случайные переменные могут быть связаны между собой, не находясь в функциональной зависимости. Такая связь называется корреляционной. В теории корреляции выделяют две основные задачи:

1) установить форму корреляционной зависимости;

2) оценить степень корреляционной зависимости.

Коэффициент корреляции служит мерой близости зависимости между двумя величинами к линейной x и y. Он рассчитывается по формуле

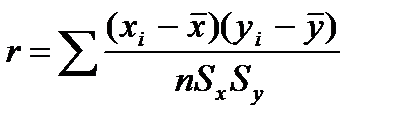(4.4.1)

Где n- число данных (пар значений x,y );

S_x - стандартное отклонение x;

S_y - стандартное отклонение y;

средние значения x и y.

Уравнение может быть записано в другой форме, которая более удобна для вычисления с помощью калькулятора

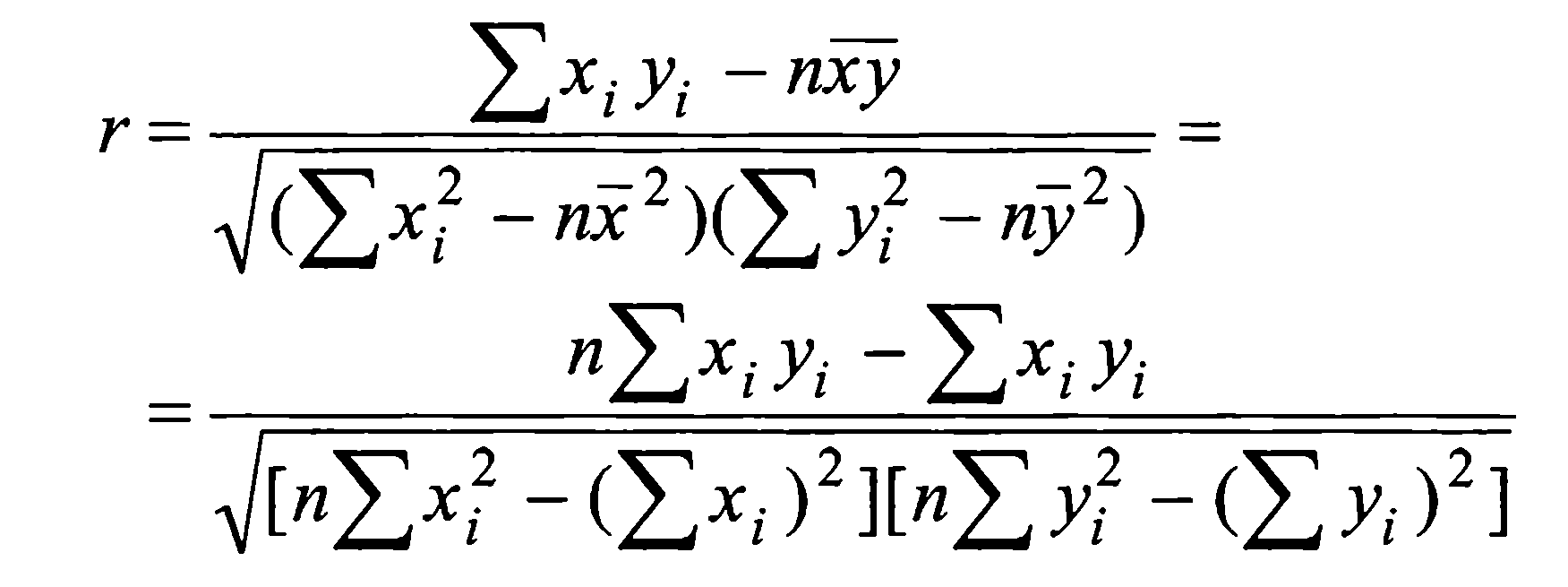(4.4.2)

Наибольшее возможное значениеrравно 1. В этом случае между двумя переменными имеется строгая линейная зависимость. Если значение r равно нулю, переменные можно считать полностью независимыми друг от друга. Наименьшее возможное значение r равно (-1). В этом случае между переменными также наблюдается строгая зависимость. Отрицательное значение коэффициента корреляции на то, что с возрастанием одной переменной другая переменная убывает.

Пример 4.С целью определения концентрации медного купороса в растворе отобрали 25 см³ пробы и прибавили к нему 10 см³ раствора KI с массовой долей 10 %. Выделившийся в эквивалентном количестве I₂ оттитровали раствором тиосульфата натрия с молярной концентрацией эквивалента 0,05 моль/дм³ амперометрически.

Уравнения протекающих при этом реакций

2Cu²⁺ + 4I^¯ = 2CuI+ I₂

I₂ + 2Na₂S₂O₃ = 2NaI + Na₂S₄O₃

Титрование проводили дозируя титрант по 0,5 см³ и записывая после каждой дозировки значение силы тока, mA. Результаты титрования в таблице 4.4.1.

Таблица-4.4.1- Результаты титрования

Рассчитатькоэффициент корреляции величин хиу.

Решение.Для удобства вычислений составим таблицу расчетных значений

Таблица-4.4.2- Расчетные значения

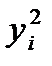
№ n/n	V(см3)Na2S2O3(x*)	I,mA (y*)			xi·yi
	0,00	56,00	0,00		0,00
	0,50	46,00	0,25		23,00
	1,00	35,00	1,00		35,00
	1,50	25,00	2,25		37,50
	2,00	14,00	4,00		28,00
	2,50	8,00	6,25		20,00
	3,00	4,00	9,00		12,00
	3,25	0,00	10,563		0,00
∑	13,75	188,00	33,313		155,50
П р и м е ч а н и е- * далее в расчетах использованы обозначения х; у

Рассчитаем среднеарифметические значения х, у

;

По формуле 4.4.2 рассчитаем коэффициент корреляции.