 |
Главная |
Свободное падение тела
|
из
5.00
|
1. В верхнем левом углу расположена стрелка. Нажмите на стрелку, перейдите к лабораторной работе № 1.5. Перед Вами график зависимости координат y от x падения тела.

2. Нажмите «Старт». Тело начинает двигаться. Справа от графика приведены значения начальных и конечных значений координат х и у, проекций скорости 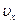 и
и 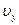 , скорости
, скорости 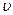 , угла
, угла  , времени падения тела t.
, времени падения тела t.
3. Значения координаты у, скорости 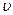 и угла
и угла  падения можно менять.
падения можно менять.
4. Можно включить стробоскоп, тогда будут отображаться направления скоростей в каждый момент времени.
5. Нажмите «Старт», пронаблюдайте движения тела с новыми параметрами.
6. Повторите моделирование необходимое количество раз (по указанию преподавателя).
7. Зарисуйте рисунок в тетрадь, запишите полученные результаты, либо распечатайте результат на принтере.
8. Ответьте на вопросы и решите задачи, расположенные в правой половине экрана.
9. Дома проработайте модель 1.8 из раздела «Модели».
10. Кликните мышью «Журнал». Обнулите результаты в таблице, нажав кнопку «Сброс результатов».
11. Проведите минитестирование. Ответьте на вопросы из раздела «Вопросы» и решите задачи из раздела «Задачи». Результат сообщите преподавателю.
12. Напишите вывод.
3. Контрольные вопросы
1. Какое движение называется равноускоренным?
2. Закон равноускоренного движения.
3. Что называется скоростью и ускорением?
4. Что называется свободным падением?
5. Что такое ускорение свободного падения?
6. От чего зависит ускорение свободного падения?
7. Как меняется траектория движения тела в зависимости от начального угла падения тела?
8. От чего зависит время и дальность полета тела?
9. От чего зависит максимальная высота подъема тела?
Лабораторная работа № 3
ДИНАМИКА МАТЕРИАЛЬНОЙ ТОЧКИ И ТВЕРДОГО ТЕЛА.
Движение брусков
Цель работы: изучение динамики поступательного движения материальной точки, движения брусков, моделей.
Краткая теория
При движении тела по траектории его скорость  может изменяться по модулю и направлению. Это означает, что тело двигается с некоторым ускорением
может изменяться по модулю и направлению. Это означает, что тело двигается с некоторым ускорением 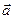 . В кинематике не ставится вопрос о физической причине, вызвавшей ускорение движения тела. Как показывает опыт, любое изменение скорости тела возникает под влиянием других тел. Динамика рассматривает действие одних тел на другие как причину, определяющую характер движения тел.
. В кинематике не ставится вопрос о физической причине, вызвавшей ускорение движения тела. Как показывает опыт, любое изменение скорости тела возникает под влиянием других тел. Динамика рассматривает действие одних тел на другие как причину, определяющую характер движения тел.
Взаимодействием тел принято называть взаимное влияние тел на движение каждого из них.
Раздел механики, изучающий законы взаимодействия тел, называетсядинамикой.
Законы динамики были открыты великим ученым И. Ньютоном (1687 г.). Три закона динамики, сформулированные Ньютоном, лежат в основе так называемой классической механики. Законы Ньютона следует рассматривать как обобщение опытных фактов. Выводы классической механики справедливы только при движении тел с малыми скоростями, значительно меньшими скорости света c=3∙108 м/с.
Самой простой механической системой является изолированное тело, на которое не действуют никакие тела. Так как движение и покой относительны, в различных системах отсчета движение изолированного тела будет разным. В одной системе отсчета тело может находиться в покое или двигаться с постоянной скоростью, в другой системе это же тело может двигаться с ускорением.
Первый закон Ньютона (или закон инерции) из всего многообразия систем отсчета выделяет класс так называемых инерциальных систем.
Существуют такие системы отсчета, относительно которых изолированные поступательно движущиеся тела сохраняют свою скорость неизменной по модулю и направлению.
Свойство тел сохранять свою скорость при отсутствии действия на него других тел называется инерцией. Поэтому первый закон Ньютона называют законом инерции.
Впервые закон инерции был сформулирован Г. Галилеем (1632 г.). Ньютон обобщил выводы Галилея и включил их в число основных законов движения.
В механике Ньютона законы взаимодействия тел формулируются для класса инерциальных систем отсчета.
При описании движения тел вблизи поверхности Земли системы отсчета, связанные с Землей, приближенно можно считать инерциальными. Однако, при повышении точности экспериментов, обнаруживаются отклонения от закона инерции, обусловленные вращением Земли вокруг своей оси.
Примером тонкого механического эксперимента, в котором проявляется неинерциальность системы, связанной с Землей, служит поведение маятника Фуко. Так называется массивный шар, подвешенный на достаточно длинной нити и совершающий малые колебания около положения равновесия. Если бы система, связанная с Землей, была инерциальной, плоскость качаний маятника Фуко оставалась бы неизменной относительно Земли. На самом деле плоскость качаний маятника вследствие вращения Земли поворачивается, и проекция траектории маятника на поверхность Земли имеет вид розетки (рис. 1.1).
 Рис. 1.1. Поворот плоскости качаний маятника Фуко.
Рис. 1.1. Поворот плоскости качаний маятника Фуко.
| С высокой степенью точности инерциальной является гелиоцентрическая система отсчета (или система Коперника), начало которой помещено в центр Солнца, а оси направлены на далекие звезды. Эту систему использовал Ньютон при открытии закона всемирного тяготения (1682 г.). Инерциальных систем существует бесконечное множество. Система отсчета, связанная с поездом, идущим с постоянной скоростью по прямолинейному участку пути, – тоже инерциальная система (приближенно), |
как и система, связанная с Землей.
Все инерциальные системы отсчета образуют класс систем, которые движутся друг относительно друга равномерно и прямолинейно. Ускорения какого-либо тела в разных инерциальных системах одинаковы.
Итак, причиной изменения скорости движения тела в инерциальной системе отсчета всегда является его взаимодействие с другими телами. Для количественного описания движения тела под воздействием других тел необходимо ввести две новые физические величины – инертную массу тела и силу.
Масса – это свойство тела, характеризующее его инертность. При одинаковом воздействии со стороны окружающих тел одно тело может быстро изменять свою скорость, а другое в тех же условиях – значительно медленнее. Принято говорить, что второе из этих двух тел обладает большей инертностью, или, другими словами, второе тело обладает большей массой.
Если два тела взаимодействуют друг с другом, то в результате изменяется скорость обоих тел, т.е. в процессе взаимодействия оба тела приобретают ускорения. Отношение ускорений двух данных тел оказывается постоянным при любых воздействиях. В физике принято, что массы взаимодействующих тел обратно пропорциональны ускорениям:

| (1.1) |
В этом соотношении величины а1 и а2 следует рассматривать как проекции векторов  и
и  на ось OX (рис. 1.2). Знак «минус» в правой части формулы означает, что ускорения взаимодействующих тел направлены в противоположные стороны.
на ось OX (рис. 1.2). Знак «минус» в правой части формулы означает, что ускорения взаимодействующих тел направлены в противоположные стороны.
В Международной системе единиц (СИ) масса тела измеряется в килограммах (кг).
Масса любого тела может быть определена на опыте путем сравнения с массой эталона (mэт = 1 кг). Пусть m1 = mэт = 1 кг. Тогда

| (1.2) |
Масса тела – скалярная величина. Опыт показывает, что если два тела с массами m1 и m2 соединить в одно, то масса m составного тела оказывается равной сумме масс m1 и m2 этих тел:
| m = m1 + m2. | (1.3) |
Это свойство масс называют аддитивностью.
 Рис. 1.2. Сравнение масс двух тел.
Рис. 1.2. Сравнение масс двух тел.
| Сила – это количественная мера взаимодействия тел. Сила является причиной изменения скорости тела. В механике Ньютона силы могут иметь различную физическую причину: сила трения, сила тяжести, упругая сила и т. д. Сила является векторной величиной. |
Векторная сумма всех сил, действующих на тело, называется равнодействующей силой. Для измерения сил необходимо установить эталон силы и способ сравнения других тел с этим эталоном.
В качестве эталона силы можно взять пружину, растянутую до некоторой заданной длины. Модуль силы F0, с которой эта пружина при фиксированном растяжении действует на прикрепленное к ее концу тело, называют эталоном силы. Способ сравнения других тел с эталоном состоит в следующем: если тело под действием измеряемой силы  и эталонной силы
и эталонной силы  остается в покое (или движется равномерно и прямолинейно), то силы равны по модулю F = F0 (рис. 1.3).
остается в покое (или движется равномерно и прямолинейно), то силы равны по модулю F = F0 (рис. 1.3).
Если измеряемая сила F больше (по модулю) эталонной силы, то можно соединить две эталонные пружины параллельно (рис. 1.4). В этом случае измеряемая сила равна 2F0. Аналогично могут быть измерены силы 3F0, 4F0 и т. д.
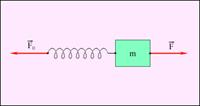 Рис. 1.3. Сравнение силы
Рис. 1.3. Сравнение силы  с эталоном с эталоном  . .
|  Рис. 1.4. Сравнение силы
Рис. 1.4. Сравнение силы  с эталоном. с эталоном.  . .
|
Измерение сил, меньших 2F0, может быть выполнено по схеме, показанной на рис. 1.5.
 Рис. 1.5. Сравнение силы
Рис. 1.5. Сравнение силы  с эталоном. с эталоном.  . .
|  Рис. 1.6. Измерение силы по растяжению пружины. При равновесии
Рис. 1.6. Измерение силы по растяжению пружины. При равновесии 
|
Эталонная сила в Международной системе единиц называется ньютон (Н).
На практике нет необходимости все измеряемые силы сравнивать с эталоном силы. Для измерения сил используют пружины, откалиброванные описанным выше способом. Такие откалиброванные пружины называются динамометрами. Сила измеряется по растяжению динамометра (рис. 1.6).
Второй закон Ньютона – основной закон динамики. Этот закон выполняется только в инерциальных системах отсчета.
Приступая к формулировке второго закона, следует вспомнить, что в динамике вводятся две новые физические величины – масса тела m и сила  , а также способы их измерения. Первая из этих величин – масса m – является количественной характеристикой инертных свойств тела. Она показывает, как тело реагирует на внешнее воздействие. Вторая – сила
, а также способы их измерения. Первая из этих величин – масса m – является количественной характеристикой инертных свойств тела. Она показывает, как тело реагирует на внешнее воздействие. Вторая – сила  – является количественной мерой действия одного тела на другое.
– является количественной мерой действия одного тела на другое.
Второй закон Ньютона – это фундаментальный закон природы; он является обобщением опытных фактов, которые можно разделить на две категории:
Если на тела разной массы подействовать одинаковой силой, то ускорения, приобретаемые телами, оказываются обратно пропорциональны массам:

| (1.4) |
Если силами разной величины подействовать на одно и то же тело, то ускорения тела оказываются прямо пропорциональными приложенным силам:
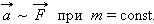
| (1.5) |
Обобщая подобные наблюдения, Ньютон сформулировал основной закон динамики:
Сила, действующая на тело, равна произведению массы тела на сообщаемое этой силой ускорение:
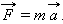
| (1.6) |
Это и есть второй закон Ньютона. Он позволяет вычислить ускорение тела, если известна его масса m и действующая на тело сила  :
:

| (1.7) |
В Международной системе единиц (СИ) за единицу силы принимается сила, которая сообщает телу массой 1 кг ускорение 1 м/с2. Эта единица называется ньютоном (Н). Ее принимают в СИ за эталон силы:
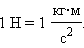
|
Если на тело одновременно действуют несколько сил (например,  , то под силой
, то под силой  в формуле, выражающей второй закон Ньютона, нужно понимать равнодействующую всех сил:
в формуле, выражающей второй закон Ньютона, нужно понимать равнодействующую всех сил:

| (1.8) | ||||
 Рис. 1.7. Сила
Рис. 1.7. Сила  – равнодействующая силы тяжести – равнодействующая силы тяжести  и силы нормального давления и силы нормального давления 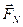 действующих на лыжницу на гладкой горе. Сила действующих на лыжницу на гладкой горе. Сила  вызывает ускорение лыжника. вызывает ускорение лыжника.
| Если равнодействующая сила 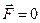 , то тело будет оставаться в состоянии покоя или равномерного прямолинейного движения. Таким образом, формально второй закон Ньютона включает как частный случай первый закон Ньютона, однако первый закон Ньютона имеет более глубокое физическое содержание – он постулирует существование инерциальных систем отсчета. , то тело будет оставаться в состоянии покоя или равномерного прямолинейного движения. Таким образом, формально второй закон Ньютона включает как частный случай первый закон Ньютона, однако первый закон Ньютона имеет более глубокое физическое содержание – он постулирует существование инерциальных систем отсчета.
| ||||
Выше понятие массы тела было введено на основе опытов по измерению ускорений двух взаимодействующих тел: массы взаимодействующих тел обратно пропорциональны численным значениям ускорений

|
Изучите модель «Движение тел на легком блоке».

| Модель позволяет изучать второй закон Ньютона на примере движения двух тел, связанных невесомой нерастяжимой нитью, перекинутой через легкий блок. Можно изменять массы тел и массу дополнительного груза Δm и наблюдать за ускоренным движением системы. |
| Модель. Движение тел на легком блоке. |
В векторной форме это соотношение принимает вид
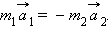
| (1.9) |
Знак «минус» выражает здесь тот опытный факт, что ускорения взаимодействующих тел всегда направлены в противоположные стороны. Согласно второму закону Ньютона, ускорения тел вызваны силами 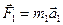 и
и  возникающими при взаимодействии тел. Отсюда следует:
возникающими при взаимодействии тел. Отсюда следует:

| (1.10) |
Это равенство называется третьим законом Ньютона.
Тела действуют друг на друга с силами, равными по модулю и противоположными по направлению.
Силы, возникающие при взаимодействии тел, всегда имеют одинаковую природу. Они приложены к разным телам и поэтому не могут уравновешивать друг друга. Складывать по правилам векторного сложения можно только силы, приложенные к одному телу.
Рис. 1.8 иллюстрирует третий закон Ньютона. Человек действует на груз с такой же по модулю силой, с какой груз действует на человека. Эти силы направлены в противоположные стороны. Они имеют одну и ту же физическую природу – это упругие силы каната. Сообщаемые обоим телам ускорения обратно пропорциональны массам тел.
Силы, действующие между частями одного и того же тела, называются внутренними. Если тело движется как целое, то его ускорение определяется только внешней силой. Внутренние силы исключаются из второго закона Ньютона, так как их векторная сумма равна нулю.
 Рис. 1.8. Третий закон Ньютона.
Рис. 1.8. Третий закон Ньютона.
| В качестве примера рассмотрим рис. 1.9, на котором изображены два тела с массами m1 и m2, жестко связанные между собой невесомой нерастяжимой нитью и двигающиеся с одинаковым ускорением 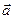 как единое целое под действием внешней силы как единое целое под действием внешней силы  . Между телами действуют . Между телами действуют
|
внутренние силы, подчиняющиеся третьему закону Ньютона:  . Движение каждого тела зависит от сил взаимодействия между ними. Второй закон Ньютона, примененный к каждому телу в отдельности, дает:
. Движение каждого тела зависит от сил взаимодействия между ними. Второй закон Ньютона, примененный к каждому телу в отдельности, дает:

| (1.11) |
Складывая левые и правые части этих уравнений и принимая во внимание, что  и
и 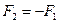 , получим:
, получим:

| (1.12) |
Внутренние силы исключились из уравнения движения системы двух связанных тел.

|
| Рис. 1.9. Исключение внутренних сил. |
Изучите модель «Движение связанных брусков».
 Модель. Движение связанных брусков.
Модель. Движение связанных брусков.
| Модель иллюстрирует третий закон Ньютона на примере движения связанных брусков под действием силы тяжести одного из них. Блоки связаны невесомой нерастяжимой нитью, перекинутой через легкий блок. Изменяя массу брусков, можно наблюдать движение системы с различными ускорениями. Обратите внимание на силы, приложенные к брускам. Убедитесь в том, что упругие силы, действующие на бруски со стороны нити, одинаковы по модулю и направлены в противоположные стороны: 
|
|
из
5.00
|
Обсуждение в статье: Свободное падение тела |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

