Модуль 1. Предмет теории вероятностей. Методы вычисления вероятностей. Случайная величина

Пример1. В коробке находится 10 шаров. 3 из них красные, 2 – зеленые, остальные белые. Найти вероятность того, что вынутый наугад шар будет красным, зеленым или белым.

Решение. Появление красного, зеленого и белого шаров составляют полную группу событий. Обозначим появление красного шара – событие А, появление зеленого – событие В, появление белого – событие С.

Тогда в соответствием с записанными выше формулами получаем:

.

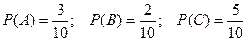Пример 2. Вероятность того, что взятая наугад деталь из некоторой партии деталей, будет бракованной равна 0,2. Найти вероятность того, что из трех взятых деталей 2 окажется не бракованными.

Решение. Обозначим бракованную деталь – событие А, не бракованную – событие .

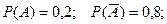
Если среди трех деталей оказывается только одна бракованная, то это возможно в одном из трех случаев: бракованная деталь будет первой, второй или третьей.

.

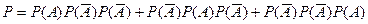
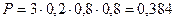Пример 3. Один из трех стрелков производит два выстрела. Вероятность попадания в цель при одном выстреле для первого стрелка равна 0,4, для второго – 0,6, для третьего – 0,8. Найти вероятность того, что в цель попадут два раза.

Решение. Вероятность того, что выстрелы производит первый, второй или третий стрелок равна .

Вероятности того, что один из стрелков, производящих выстрелы, два раза попадает в цель, равны:

- для первого стрелка:

- для второго стрелка:

- для третьего стрелка:

Искомая вероятность равна:

.

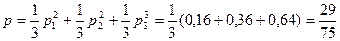Пример 4. Трое охотников одновременно выстрелили по медведю, который был убит одной пулей. Определить вероятность того, что медведь был убит первым стрелком, если вероятности попадания для этих стрелков равны соответственно 0,3, 0,4, 0,5.

Решение. В этой задаче требуется определить вероятность гипотезы уже после того, как событие уже совершилось. Для определения искомой вероятности надо воспользоваться формулой Бейеса. В нашем случае она имеет вид:

 

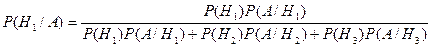
В этой формуле Н₁, Н₂, Н₃ – гипотезы, что медведя убьет первый, второй и третий стрелок соответственно. До произведения выстрелов эти гипотезы равновероятны и их вероятность равна .

P(H₁/A) – вероятность того, что медведя убил первый стрелок при условии, что выстрелы уже произведены (событие А).

Вероятности того, что медведя убьет первый, второй или третий стрелок, вычисленные до выстрелов, равны соответственно:

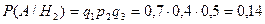
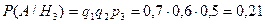
Здесь q₁ = 0,7; q₂ = 0,6; q₃ = 0,5 – вероятности промаха для каждого из стрелков, рассчитаны как q = 1 – p, где р – вероятности попадания для каждого из стрелков.

Подставим эти значения в формулу Бейеса:

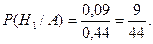
Пример 5. По цели производится 5 выстрелов. Вероятность попадания для каждого выстрела равна 0,4. Найти вероятность того, что в цель попали не менее трех раз.

Решение. Вероятность не менее трех попаданий складывается из вероятности пяти попаданий, четырех попаданий и трех попаданий.

Т.к. выстрелы независимы, то можно применить формулу Бернулли вероятности того, что в т испытаниях событие в вероятностью р наступает ровно п раз.

.

В случае пяти попаданий из пяти возможных:

.

Четыре попадания из пяти выстрелов:

.

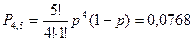Три попадания из пяти:

.

Окончательно, получаем вероятность не менее трех попаданий из пяти выстрелов:

.

Пример 6. В партии 10% нестандартных деталей. Наугад отобраны 4 детали. Написать биноминальный закон распределения дискретной случайной величины Х – числа нестандартных деталей среди четырех отобранных и построить многоугольник полученного распределения.

Решение. Вероятность появления нестандартной детали в каждом случае равна 0,1.

Найдем вероятности того, что среди отобранных деталей:

1) Вообще нет нестандартных.

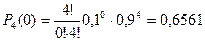
2) Одна нестандартная.

3) Две нестандартные детали.

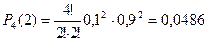
4) Три нестандартные детали.

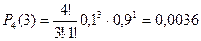
5) Четыре нестандартных детали.

.

Пример 7. Испытывается устройство, состоящее из четырех независимо работающих приборов. Вероятности отказа каждого из приборов равны соответственно р₁=0,3; p₂=0,4; p₃=0,5; p₄=0,6. Найти математическое ожидание и дисперсию числа отказавших приборов.

Решение. Принимая за случайную величину число отказавших приборов, видим что эта случайная величина может принимать значения 0, 1, 2, 3 или 4.

Для составления закона распределения этой случайной величины необходимо определить соответствующие вероятности. Примем .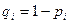

1) Не отказал ни один прибор.

2) Отказал один из приборов.

0,302.

3) Отказали два прибора.

4) Отказали три прибора.

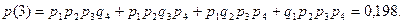
5) Отказали все приборы.

Получаем закон распределения:

 

X
X2
P	0,084	0,302	0,38	0,198	0,036

Математическое ожидание:

 

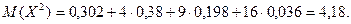
Дисперсия:

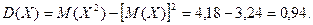
Пример 8. Задана непрерывная случайная величина х своей функцией распределения f(x).

Требуется определить коэффициент А, найти функцию распределения, построить графики функции распределения и плотности распределения, определить вероятность того, что случайная величина х попадет в интервал .

Решение. Найдем коэффициент А.

Найдем функцию распределения:

1) На участке :

2) На участке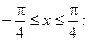

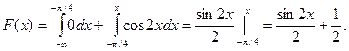
3) На участке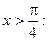

Итого: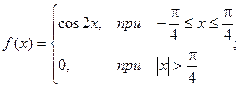

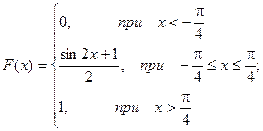
Построим график плотности распределения:

Найдем вероятность попадания случайной величины в интервал .

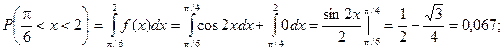
Ту же самую вероятность можно искать и другим способом:

 

f(x)

 

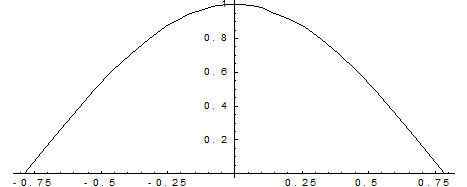
Построим график функции распределения:

 

 

F(x)

 

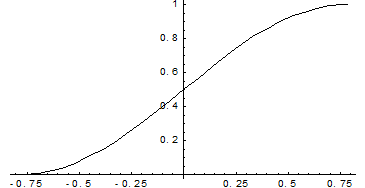
Пример 9. Для рассмотренного выше примера 8 определить математическое ожидание и дисперсию случайной величины Х.

Решение.

Образцы вариантов контрольной работы по теме «Случайные события»

Вариант 1

1. В ящике среди 10 одинаковых по внешнему виду деталей имеется 8 стандартных. Наудачу взяты три детали. Составить полную группу возможных событий и найти их вероятности.

2. Вероятность того, что студент сдает первый экзамен, равна 0,9; второй экзамен – 0,85; третий экзамен – 0,95. Найти вероятности событий:

а) студент сдаст все три экзамена;

б) сдаст не менее двух экзаменов;

в) не сдаст только третий экзамен.

3. На склад поступают изделия трех заводов, производительности которых относятся как 1:2:1. Вероятность изготовления первосортного изделия на 1-м заводе равна 0,8; на 2-м заводе – 0,7; на 3-м – 0,9. Наудачу взятое изделие оказалось первосортным. Найти вероятность того, что оно изготовлено на первом заводе.

4. Контрольная работа состоит из шести задач, причем для «зачета» необходимо решить любые четыре задачи. Если студент будет решать в течение отведенного времени лишь четыре задачи, то вероятность правильного решения любой из них равна 0,8. Если он попробует решать пять задач, то вероятность правильного решения любой из них равна 0,7, а если он возьмется за решение всех шести задач, то вероятность снизится до 0,6. Какой тактики должен придерживаться студент, чтобы иметь наибольшие шансы получить зачет?

 

Вариант 2

1. В коробке 5 красных, 3 синих и 2 желтых карандаша. Наудачу взяли три карандаша. Найти вероятности событий:

а) среди выбранных карандашей – 2 красных и 1 синий;

б) эти карандаши одного цвета;

в) разных цветов.

2. Вероятность попадания стрелком в цель при выстреле равна 0,7. Стрелок стреляет до первого попадания. Чему равна вероятность того, что ему потребуется:

а) три выстрела;

б) не более трех выстрелов?

3. Половина поступивших на склад изделий изготовлена на первом заводе, третья часть – на втором заводе. Остальные изделия – на третьем. Первый завод производит 1 % с браком, второй – 0,7 % и третий – 0,5 %. Произвольно выбранное изделие оказалось с браком. Какова вероятность того, что оно изготовлено:

а) на первом заводе;

б) на втором заводе.

4. Что вероятнее: выиграть у равносильного противника (ничейный исход партии исключается) три партии из четырех или пять из восьми?

 

Вариант 3

1. Брошены две игральные кости. Найти вероятность того, что сумма выпавших очков:

а) равна пяти;

б) больше десяти.

2. В экзаменационном билете 3 вопроса. Вероятность того, что студент ответит на первый вопрос, равна 0,95, на второй вопрос – 0,9 и на третий вопрос – 0,85. Определить вероятность того, что студент сдаст экзамен, если для этого ему необходимо ответить хотя бы на два вопроса.

3. В классе обучаются 20 девочек и 10 мальчиков. К уроку не выполнили домашнее задание 4 девочки и 3 мальчика. Наудачу вызванный ученик оказался неподготовленным к уроку. Какова вероятность того, что отвечать был вызван мальчик?

4. На каждое из 6 заданий теста даны пять ответов, из которых один верный. Чему равна вероятность, что студент угадает ответы трех заданий? Чему равна вероятность, что студент получит «зачет», отвечая наудачу, если должны быть получены не менее четырех верных ответов?

 

Вариант 4

1. На группу из 10 юношей и 14 девушек выдали 6 билетов в театр. Какова вероятность, что при случайном распределении билетов

а) в группе «театралов» окажется поровну юношей и девушек;

б) все билеты достанутся девушкам?

2. Имеются две урны: в первой 4 белых и 2 черных шара, во второй 6 белых и 4 черных. Из первой урны во вторую перекладывают, не глядя, два шара. Затем из второй урны берут один шар. Найти вероятность того, что шар будет белым.

3. Три орудия ведут стрельбу по цели. Вероятности попадания в цель для них соответственно равны 0,4; 0,5; 0,55. Для поражения цели достаточно двух попаданий. Орудия сделали залп по цели. Найти вероятность того, что цель будет поражена. Вычислить вероятность того, что хотя бы одно оружие попадет в цель.

4. Вероятность преждевременного перегорания электролампы составляет 0,02. Найти вероятность того, что не менее 4 из 6 ламп перегорит преждевременно. Найти вероятность того, что из 100 электроламп перегорит:

а) три лампы;

б) хотя бы одна лампа.

 

Вариант 5

1. Подсчитать вероятность того, что в наудачу выбранном телефонном номере, состоящем из 6 цифр, все цифры окажутся различными.

2. Рабочий обслуживает три станка. Вероятность того, что в течение смены потребует его внимания первый станок, равна 0,7; второй – 0,75; третий – 0,8. Найти вероятность того, что в течение смены внимания рабочего потребуют:

а) какие-либо два станка;

б) хотя бы один станок.

3. Изделия изготавливаются на трех станках-автоматах. Первый производит 40 %, второй – 50 %, а третий 10 % всех изделий. Брак в их продукции составляет соответственно 3 %, 4 %, 1 %. Случайно выбранное изделие оказалось стандартным. Найти вероятность того, что оно произведено:

а) первым станком-автоматом;

б) вторым станком-автоматом.

4. Пусть вероятность того, что покупателю необходима обувь 41-го размера, равна 0,2. Найти вероятность того, что из пяти первых покупателей обувь этого размера будет необходима:

а) одному покупателю;

б) по крайней мере одному.