Частные производные второго порядка функции трёх переменных

 

Общий принцип нахождения частных производных порядка второго порядка функции трёх переменных аналогичен принципу нахождения частных производных 2-го порядка функции двух переменных.

Для того чтобы найти частные производные второго порядка, необходимо сначала найти частные производные первого порядка или, в другой записи:

.

Частных производных второго порядка девять штук.

Первая группа – это вторые производные по тем же переменным:

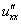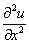или – вторая производная по «икс»;

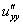или – вторая производная по «игрек»;

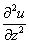или – вторая производная по «зет».

Вторая группа – это смешанные частные производные 2-го порядка, их шесть:

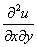или – смешанная производная «по икс игрек»;

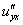или – смешанная производная «по игрек икс»;

или – смешанная производная «по икс зет»;

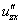или – смешанная производная «по зет икс»;

или – смешанная производная «по игрек зет»;

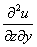или – смешанная производная «по зет игрек».

Как и для случая функции двух переменных, при решении задач можно ориентироваться на следующие равенства смешанных производных второго порядка:

.

 

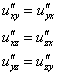Примечание: строго говоря, это не всегда так. Для равенства смешанных производных необходимо выполнение требования их непрерывности.

 

На всякий случай несколько примеров, как правильно читать сиё безобразие вслух:

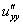– «у два штриха дважды по игрек»;

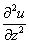– «дэ два у по дэ зет квадрат»;

– «у два штриха по икс по зет»;

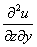– «дэ два у по дэ зет по дэ игрек».

 

Пример 10

Найти все частные производные первого и второго порядка для функции трёх переменных:

.

Решение:Сначала найдем частные производные первого порядка:

Частные производные второго порядка рекомендую начинать искать со смешанных производных, поскольку это позволит выяснить, а правильно ли вообще найдены производные первого порядка.

Берём найденную производную

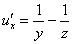
и дифференцируем её по «игрек»:

Берём найденную производную

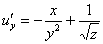
и дифференцируем её по «икс»:

Равенство 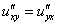выполнено. Хорошо.

Разбираемся со второй парой смешанных производных.

Берём найденную производную

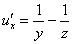
и дифференцируем её по «зет»:

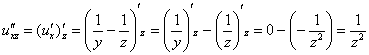
Берём найденную производную

и дифференцируем её по «икс»:

Равенство 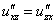выполнено. Хорошо.

Аналогично разбираемся с третьей парой смешанных производных:

Равенство 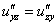выполнено. Хорошо.

 

После проделанных трудов гарантированно можно утверждать, что, во-первых, мы правильно нашли все частные производные 1-го порядка, во-вторых, правильно нашли и смешанные частные производные 2-го порядка.

 

Осталось найти ещё три частные производные второго порядка, вот здесь уже во избежание ошибок следует максимально сконцентрировать внимание:

Готово. Повторюсь, задание не столько сложное, сколько объемное. Решение можно сократить и сослаться на равенства смешанных частных производных, но в этом случае не будет проверки. Поэтому лучше потратить время и найти всепроизводные (к тому же это может потребовать преподаватель), или, в крайнем случае, выполнить проверку на черновике.

 

Пример 11

Найти все частные производные первого и второго порядка для функции трёх переменных

.

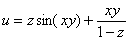Это пример для самостоятельного решения.

 

 

Решения и ответы:

Пример 2: Решение:

 

Пример 4:Решение:Найдем частные производные первого порядка.

Составим полный дифференциал первого порядка:

Пример 6: Решение: Вычислим частные производные первого порядка в точке M(1, -1, 0):

 

Пример 7: Решение: Вычислим частные производные первого порядка в точке M(1, 1, 1):

 

Пример 9: Решение: Найдем частные производные первого порядка:

 

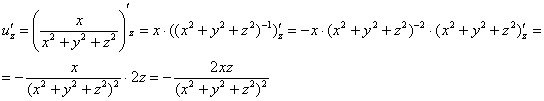
Пример 11: Решение:Найдем частные производные первого порядка:

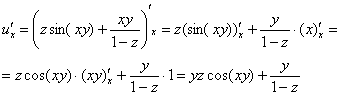
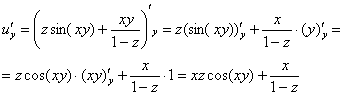
Найдем частные производные второго порядка:

.

 

 

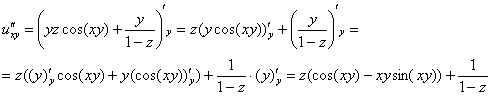
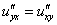
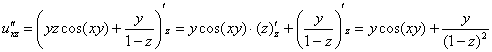
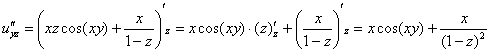
Интегралы