Метод замены переменной в неопределенном интеграле. Примеры решений

 

На данном уроке мы познакомимся с одним из самых важных и наиболее распространенных приемов, который применяется в ходе решения неопределенных интегралов – методом замены переменной. Для успешного освоения материала требуются начальные знания и навыки интегрирования. Если есть ощущение пустого полного чайника в интегральном исчислении, то сначала следует ознакомиться с материалом Неопределенный интеграл. Примеры решений, где объяснено в доступной форме, что такое интеграл и подробно разобраны базовые примеры для начинающих.

Технически метод замены переменной в неопределенном интеграле реализуется двумя способами:

– Подведение функции под знак дифференциала.

– Собственно замена переменной.

По сути дела, это одно и то же, но оформление решения выглядит по-разному. Начнем с более простого случая.

 

 

Подведение функции под знак дифференциала

 

На уроке Неопределенный интеграл. Примеры решениймы научились раскрывать дифференциал. Напоминаем пример, который мы приводили:

.

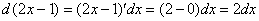То есть, раскрыть дифференциал – это почти то же самое, что найти производную.

 

Пример 1

Найти неопределенный интеграл.

.

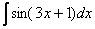Выполнить проверку.

Смотрим на таблицу интегралов и находим похожую формулу:

.

Но проблема заключается в том, что у нас под синусом не просто буковка «икс», а сложное выражение. Что делать?

Подводим функцию (3x + 1) под знак дифференциала:

.

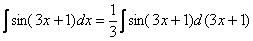Раскрывая дифференциал, легко проверить, что, действительно, проведено тождественное преобразование:

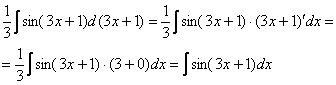
Фактическ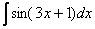и

и 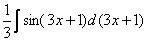– это запись одного и того же.

Но, тем не менее, остался вопрос, а как мы пришли к мысли, что на первом шаге нужно записать наш интеграл именно так: .

Почему так, а не иначе?

 

Формула и все другие табличные формулы справедливы и применимы НЕ ТОЛЬКО для переменнойx, но и для любого сложного выражения ЛИШЬ БЫ АРГУМЕНТ ФУНКЦИИ(в нашем примере - это 3x + 1) И ВЫРАЖЕНИЕ ПОД ЗНАКОМ ДИФФЕРЕНЦИАЛА БЫЛИ ОДИНАКОВЫМИ.

 

Поэтому мысленное рассуждение при решении должно складываться примерно так:

 

«Мне надо решить интеграл 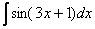. Я посмотрел в таблицу и нашел похожую формулу . Но у меня сложный аргумент (3x + 1) и формулой я сразу воспользоваться не могу. Но если мне удастся получить (3x + 1) и под знаком дифференциала, то всё будет нормально. Если я запишу d(3x + 1), тогда: d(3x + 1) = (3x + 1)’dx = 3dx.

Но в исходном интеграле

множителя-тройки нет, поэтому, чтобы подынтегральная функция не изменилась, мне надо её домножить на (1/3)».

 

В ходе примерно таких мысленных рассуждений и рождается запись:

.

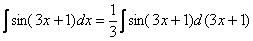Теперь можно пользоваться табличной формулой :

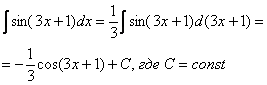
Готово. Единственное отличие: у нас не буква «икс», а сложное выражение (3x + 1).

 

Выполним проверку. Открываем таблицу производных и дифференцируем ответ:

Получена исходная подынтегральная функция, значит, интеграл найден правильно.

 

Обратите внимание, что в ходе проверки мы использовали правило дифференцирования сложной функции .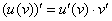

По сути дела, подведение функции под знак дифференциала и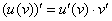 – это два взаимно обратных правила.

 

Пример 2

Найти неопределенный интеграл

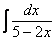. Выполнить проверку.

Анализируем подынтегральную функцию. Здесь у нас дробь, причем в знаменателе линейная функция (с «иксом» в первой степени). Смотрим в таблицу интегралов и находим наиболее похожую вещь:

.

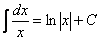Подводим функцию (5 - 2x) под знак дифференциала:

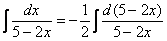
Те, кому трудно сразу сообразить, на какую дробь нужно домножать, могут быстренько на черновике раскрыть дифференциал: .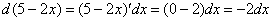

Получается -2dx, значит, чтобы ничего не изменилось, надо домножить интеграл на (-1/2).

Далее используем табличную формулу

:

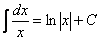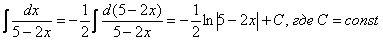Проверка:

Получена исходная подынтегральная функция, значит, интеграл найден правильно.

 

Пример 3

Найти неопределенный интеграл

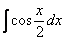. Выполнить проверку.

Это пример для самостоятельного решения. Ответ в конце урока.

 

Пример 4

Найти неопределенный интеграл

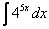. Выполнить проверку.

Это пример для самостоятельного решения. Ответ в конце урока.

 

При определенном опыте решения интегралов, подобные примеры будут казаться лёгкими, и щелкаться как орехи:

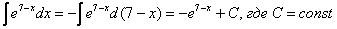
И так далее.

 

В конце данного параграфа хотелось бы еще остановиться на случае, когда в линейной функции переменная x входит с единичным коэффициентом, например:

.

Строго говоря, решение должно выглядеть так:

.

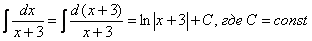Как видите, подведение функции (x+3)под знак дифференциала прошло «безболезненно», без всяких домножений. Поэтому на практике таким длинным решением часто пренебрегают и сразу записывают, что . Но будьте готовы при необходимости объяснить преподавателю, как Вы решали! Поскольку интеграла в таблице вообще-то нет.