 |
Главная |
Вычисление площади круга с помощью определенного интеграла. Тригонометрическая подстановка
|
из
5.00
|
Это очень важная задача, поскольку будет рассмотрен типовой интеграл и приём решения, который неоднократно встретится в будущем.
Но сначала небольшое напоминание по уравнению окружности. Уравнение вида  задаёт окружность с центром в точке
задаёт окружность с центром в точке 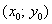 радиуса
радиуса  .
.
В частности, уравнение  задаёт окружность радиуса
задаёт окружность радиуса  с центром в начале координат, в точке (0; 0).
с центром в начале координат, в точке (0; 0).
Пример 4
Вычислить площадь круга, ограниченного окружностью с уравнением  . Выполним чертёж:
. Выполним чертёж:

Сначала вычислим площадь круга с помощью известной школьной формулы. Если радиус круга  , то его площадь равна: S = π∙r2 = π∙22 = 4π ед2.
, то его площадь равна: S = π∙r2 = π∙22 = 4π ед2.
Для того, чтобы вычислить площадь круга с помощью определенного интеграла, необходимо из уравнения  выразить функцию «игрек» от «икс» в явном виде:
выразить функцию «игрек» от «икс» в явном виде:
Верхняя полуокружность задается уравнением  .
.
Нижняя полуокружность задается уравнением 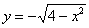 .
.
Можно подставить несколько точек окружности в эти уравнения и убедиться в справедливости вышеизложенных утверждений.
Как вычислить площадь круга? В данном примере круг симметричен относительно начала координат, поэтому достаточно вычислить площадь одного сектора в 1-ой четверти (заштрихован синим цветом), а затем результат умножить на 4. Таким образом:
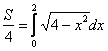 .
.
Такой же, но неопределенный интеграл рассматривался в Примере 6 раздела Сложные интегралы, он решался длительным и трудоёмким методом сведения интеграла к самому себе. Можно пойти тем же путём, но для определенного интеграла существует удобный и эффективный метод тригонометрической замены:
Проведём замену: 
Почему именно такая замена, очень скоро станет понятно, а пока найдем дифференциал:

Выясним, во что превратится корень, который распишем очень подробно:
 .
.
Если в ходе решения вы не сможете догадаться применить формулу наподобие  , то, увы, получите: «Приходите в следующий раз».
, то, увы, получите: «Приходите в следующий раз».
После преобразования корня отчетливо видно, почему проведена замена  , особое внимание обращаем на коэффициент при синусе – «двойке», этот коэффициент нужно подбирать таким образом, чтобы при возведении в квадрат всё хорошо вынеслось за скобки и из-под корня.
, особое внимание обращаем на коэффициент при синусе – «двойке», этот коэффициент нужно подбирать таким образом, чтобы при возведении в квадрат всё хорошо вынеслось за скобки и из-под корня.
Осталось вычислить новые пределы интегрирования:
Если  , то
, то  .
.
Новый нижний предел интегрирования:  .
.
Новый верхний предел интегрирования:  .
.
Таким образом:
 .
.
Площадь сектора необходимо умножить на 4, следовательно, площадь всей окружности:

Вероятно, у некоторых возник вопрос, зачем вообще мучиться с интегралом, если есть короткая школьная формула S = π∙r2? А дело в том, что возможность очень точно вычислить площадь круга появилась только с развитием математического анализа, хотя уже в древности Архимед площадь круга рассчитывал с приличной точностью.
Разобранный пример можно решить в общем виде, то есть найти площадь круга, ограниченного окружностью произвольного радиуса:  . В результате получится как раз формула S = π∙r2!
. В результате получится как раз формула S = π∙r2!
Следует отметить, что к решению данной задачи можно было применить и другой подход – вычислить площадь верхнего полукруга с помощью интеграла
 ,
,
а затем удвоить результат. Но в силу чётности подынтегральной функции решение сводится к оптимальной версии:
 .
.
Еще раз подчеркнём важность проведенной тригонометрической замены, она встретится на практике не раз и не два. Поэтому, для закрепления материала, чуть - более сложное задание для самостоятельного решения:
Пример 5
Вычислить определенный интеграл
 .
.
По условию требуется вычислить определенный интеграл, поэтому чертеж выполнять не нужно. Хорошо подумайте над коэффициентом в замене  . Если возникнут трудности с интегралом после замены, вернитесь к уроку Интегралы от тригонометрических функций. Полное решение и ответ в конце урока.
. Если возникнут трудности с интегралом после замены, вернитесь к уроку Интегралы от тригонометрических функций. Полное решение и ответ в конце урока.
|
из
5.00
|
Обсуждение в статье: Вычисление площади круга с помощью определенного интеграла. Тригонометрическая подстановка |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

