Свойства треугольника Паскаля

. Числа, равноудаленные от концов треугольника Паскаля, равны.

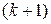. Для нахождения -го числа 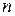-й строки треугольника Паскаля надо умножить ‑ое на и поделить на .

. Каждое число в треугольнике Паскаля равно сумме двух чисел, находящихся над ним.

. Сумма чисел n-ой строки треугольника Паскаля равна .

Свойство позволяет легко заменить в таблице обозначения 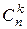конкретными числами, не пользуясь формулой числа сочетаний. Получаем следующую таблицу:

1 1

1 2 1

1 3 3 1

1 4 6 4 1

1 5 10 10 5 1

. . . . . . . . . .

Таблица 2.

Для получения этой таблицы надо на сторонах треугольника записать единицы, а внутренность угла при вершине заполнять, идя сверху вниз суммами стоящих рядом чисел предыдущей строки.

Например, число 10 в пятой строке табл. 2 получено сложением чисел 4 и 6 предыдущей строки.

Бином Ньютона

Приведем формулу для возведения суммы двух чисел в натуральную степень. Прежде всего, заметим, что числа стоящие с строках треугольника Паскаля, встречаются при возведении в степень двучлена :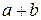

,

.

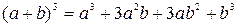Но коэффициенты 1, 2, 1 – это числа, стоящие во второй (напоминаем, что мы ведем счет с 0) строке таблицы 2, т.е. 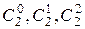, а 1, 3, 3, 1 – числа, стоящие в третьей строке той же таблицы, т.е. .

Это замечание позволяет предположить, что справедливо следующее утверждение.

Т е о р е м а 5.Длялюбых чисел и натурального числа 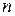справедлива формула

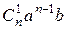= + + + … + + … + . (1)

□ Доказательство формулы (6) проведем индукцией по n, используя свойство 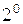сочетаний.

База индукции. При 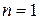имеем = = 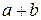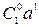+ 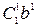и, следовательно, формула (1) справедлива.

Шаг индукции. Предположим, что формула (6) справедлива при , т.е.

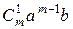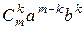= + + … + + … + . (2)

Чтобы доказать справедливость равенства (1) при , умножим обе части равенства (2) на :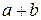

= + + … + + … + .

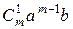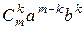Раскрывая скобки и приводя подобные в правой части последнего равенства, получаем

= + + … + + … + .

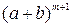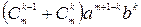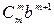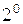Учитывая очевидные равенства = , = и свойство сочетаний, имеем

= + + … + + … + .

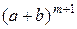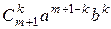Итак, формула (1) справедливо при + 1.

Вывод. Формула (1) справедлива при любом натуральном .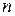

Формулу (1) называют обычно формулой бинома Ньютона, хотя она была известна задолго до Ньютона уже упоминавшемуся Гиясэддину Каши, а также Паскалю и другим. Заслуга Ньютона состоит в том, что он нашел обобщение формулы (6) на случай нецелых показателей.

Формулу (1), учитывая, что 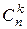= 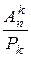, в развернутом виде можно переписатьв следующем виде:

= + + + …

…+ + … + + . ( )

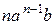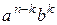С помощью формулы бинома Ньютона можно получить некоторые из доказанных ранее свойств сочетаний, а также вывести иные их свойства, и наоборот, свойства сочетаний позволяют упрощать вычисления коэффициентов в формуле (1). Числа 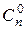, , 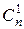…, называются биномиальными коэффициентами. Поскольку эти числа записаны в n‑ой строке треугольника Паскаля, то перефразируя его свойства получаем следующие