Выборочная дисперсия. Исправленная дисперсия

Оценка параметров генеральной совокупности

Выборочное среднее

Пусть имеется случайная выборка объема n, представленная вариационным рядом {(x_j, n_j)}, где x_j — варианты, n_j — частоты, j = 1, 2, …, m. Если мы имеем дело с интервальным вариационным рядом, то x_j — середины интервалов.

Выборочное среднее значение определяется по формуле

(3.1)

Если выборка не сгруппирована, то выборочная средняя определяется по формуле

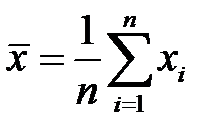(3.2)

Выборочное среднее 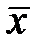является случайной величиной. Её математическое ожидание равно генеральной средней, т.е. выборочное среднее является несмещенной оценкой генеральной средней.

Если у генеральной совокупности генеральная средняя равна a и среднеквадратическое отклонение равно σ, то среднеквадратическое отклонение выборочной средней для повторной выборки вычисляется по формуле

. (3.3)

Среднеквадратическое отклонение выборочной средней для бесповторной выборки вычисляется по формуле

. (3.4)

где N — объем генеральной совокупности.

Для вычисления выборочной средней для не сгруппированной выборки в программе Excel можно воспользоваться следующей функцией (которая вычисляет среднее арифметическое):

СРЗНАЧ(число1;число2; ...)

Число1, число2, ... — это от 1 до 30 аргументов, для которых вычисляется среднее.

• Аргументы должны быть либо числами, либо именами, массивами или ссылками, содержащими числа.
• Если аргумент, который является массивом или ссылкой, содержит тексты, логические значения или пустые ячейки, то такие значения игнорируются; однако ячейки, которые содержат нулевые значения, учитываются.

Если выборка представлена вариационным рядом, то для вычисления выборочного среднего можно воспользоваться функцией СУММПРОИЗВЕД(массив1;массив2;…), которая вычисляет сумму произведений соответствующих элементов массивов массив1, массив2 и т.д.

Пример 3.1. Найти выборочное среднее для выборки из 10 числовых значений, записанных в ячейках А2:А11 (см. рис. 3.1).

Рис. 3.1

Решение. Введите в ячейку А12 формулу =СРЗНАЧ(А2:А11). Получим значение 1,9.

Пример 3.2. Найти выборочное среднее для выборки, представленной вариационным рядом из 10 числовых значений вариант, записанных в ячейках С2:С11, и 10 значений частот, записанных в ячейках D2:D11 .

Решение. Введите в ячейку C12 формулу

=СУММПРОИЗВ(C2:C11;D2:D11)/СУММ(D2:D11).

Получим значение 3,571429.

Выборочная дисперсия. Исправленная дисперсия

Выборочная дисперсия s² для сгруппированной в вариационный ряд выборки определяется по формуле

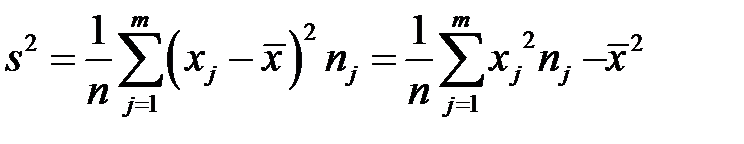(3.5)

Исправленная дисперсия вычисляется по формуле

(3.6)

Если выборка не сгруппирована, то выборочная дисперсия s² определяется по формуле

, (3.7)

а исправленная дисперсия — по формуле

(3.8)

Исправленная дисперсия является несмещенной оценкой генеральной дисперсии, т.е. математическое ожидание исправленной дисперсии равно генеральной дисперсии.

В программе Excel для вычисления выборочной дисперсии для выборки, не сгруппированной в вариационный ряд, предназначена функция

ДИСПР(число1;число2; ...)

Число1, число2,... — от 1 до 30 числовых аргументов, соответствующих выборке (числа или диапазоны ячеек).

ДИСПР предполагает, что аргументы представляют всю генеральную совокупность. Если данные представляют только выборку из генеральной совокупности, то дисперсию следует вычислять, используя функцию ДИСП.

Формула для ДИСПР имеет вид (3.7).

Для вычисления исправленной дисперсии предназначена функция

ДИСП(число1;число2; ...)

Формула для ДИСП имеет вид (3.8).

Обратите внимание на имена этих функций, можно подумать, что ДИСПР() вычисляет исправленную дисперсию, а ДИСП() — выборочную, тогда как на самом деле функция ДИСП() вычисляет исправленную дисперсию, а ДИСПР() — выборочную.