 |
Главная |
Оценка случайных погрешностей прямых равноточных измерений
|
из
5.00
|
Случайные погрешности проявляются при многократных наблюдениях измеряемой величины в одинаковых условиях. Их влияние на результат измерения надо учитывать и стремиться по возможности уменьшать.
К оценкам случайной величины, получаемым по статистическим данным, предъявляются требования состоятельности, несмещенности и эффективности. Оценка параметра Q считается состоятельной, если Q(Q1, Q2, .... Qn)→Qист, при п→∞, несмещенной, если М[Q]=Qист, эффективной, если D[Q]=min. Здесь Qi–результат i-ro наблюдения, п – число наблюдений.
Способы нахождения оценок конечного ряда наблюдений и показатели их качества зависят от законов распределения. Для нормального распределения, а если поступиться эффективностью оценки, то и для всех симметричных распределений, в качестве оценки математического ожидания ряда равноточных наблюдений принимают среднее арифметическое ряда наблюдений.

При п→∞, если отсутствует систематическая погрешность, Q→Qист. Разность vi=Qi–  представляет собой случайную погрешность при i-м наблюдении. Она может быть положительной и отрицательной.
представляет собой случайную погрешность при i-м наблюдении. Она может быть положительной и отрицательной.
Среднее арифметическое независимо от закона распределения обладает свойствами:

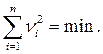
В качестве оценки дисперсии берется дисперсия отклонения результата наблюдения 
а в качестве оценки СКО результата наблюдения – 
Среднее арифметическое зависит от числа наблюдений и является случайной величиной, которая обладает некоторой дисперсией относительно истинного значения величины Qист. Оценкой дисперсии среднего арифметического ряда наблюдений относительно истинного значения является 
Величина  называется СКО результата измерений.
называется СКО результата измерений.
Таким образом, взяв за результат измерения  , уменьшаем СКО в
, уменьшаем СКО в  раз по сравнению со случаем, если бы за результат измерения принималось любое одно из n наблюдений.
раз по сравнению со случаем, если бы за результат измерения принималось любое одно из n наблюдений.
Измерения с многократными наблюдениями и соответствующая обработка результатов позволяют уменьшить случайную погрешность и оценить ее. Оценки  и
и  являются так называемыми точечными оценками случайной погрешности. Они указывают интервал значений измеряемой величины
являются так называемыми точечными оценками случайной погрешности. Они указывают интервал значений измеряемой величины  , внутри которого находится истинное значение.
, внутри которого находится истинное значение.
В отличие от точечной при интервальной оценке определяется доверительный интервал eр, в котором с доверительной вероятностью Р находится истинное значение Qист

При заданной вероятности Р и вычисленной  значение
значение  определяется законом распределения. В случае нормального распределения и числа измерений n³20
определяется законом распределения. В случае нормального распределения и числа измерений n³20  выбирается по таблице функций Лапласа.
выбирается по таблице функций Лапласа.
Если число измерений n<20, то доверительный интервал случайной погрешности при заданных вероятности Р и СКО результата измерения  определяется по формуле Стьюдента
определяется по формуле Стьюдента
 ,
,
где  – коэффициент распределения Стьюдента, который зависит от заданной вероятности Р и числа измерений n.
– коэффициент распределения Стьюдента, который зависит от заданной вероятности Р и числа измерений n.
При n³20 распределение Стьюдента приближается к нормальному, и вместо  , можно использовать
, можно использовать  для нормального распределения. Поскольку при равномерном распределении доверительный интервал слабо зависит от доверительной вероятности, обычно принимают
для нормального распределения. Поскольку при равномерном распределении доверительный интервал слабо зависит от доверительной вероятности, обычно принимают  , т.е. для P=1. Таким образом, истинное значение будет находиться внутри интервала:
, т.е. для P=1. Таким образом, истинное значение будет находиться внутри интервала:  Рассмотрим, какую же доверительную вероятность следует брать? Как правило, принимают Р=0,95. Если же измерения нельзя повторить, то принимают Р=0,99, а в особо ответственных случаях еще выше, когда проводимые измерения связаны с созданием новых эталонов или имеют значение для здоровья людей.
Рассмотрим, какую же доверительную вероятность следует брать? Как правило, принимают Р=0,95. Если же измерения нельзя повторить, то принимают Р=0,99, а в особо ответственных случаях еще выше, когда проводимые измерения связаны с созданием новых эталонов или имеют значение для здоровья людей.
Остановимся на способе исключения из результатов измерения промахов и грубых погрешностей. Если в полученной группе результатов наблюдений одно-два резко отличаются от остальных, то, прежде всего, следует проверить, нет ли описки, ошибки в снятии показаний или других промахов. Если промахи не установлены, то следует проверить, не являются ли они грубыми погрешностями. Эта задача решается статистическими методами, основанными на том, что распределение, к которому относится выборка, можно считать нормальным.
Поскольку погрешности измерений определяют лишь зону недостоверности результата, их не требуется знать очень точно. Погрешности оценок случайных погрешностей, особенно при малом числе измерений (n£10), весьма велики. Поэтому погрешности измерения в окончательной записи принято выражать числом с одной или двумя значащими цифрами. При промежуточных выкладках в числовых значениях погрешности необходимо удерживать по три-четыре значащих цифры, чтобы погрешности округления не искажали результат измерения.
|
из
5.00
|
Обсуждение в статье: Оценка случайных погрешностей прямых равноточных измерений |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

