 |
Главная |
Приложение к модели Г. Марковица
|
из
5.00
|
A. Вывод функции полезности и формулы риска для портфеля
1. Вывод квадратной функции полезности, включающей непосредственное измерение риска[39]
Полезность любого дохода 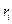 инвестиционного портфеля может быть найдена путем подстановки этого дохода в общую формулу квадратной функции полезности. В результате получим:
инвестиционного портфеля может быть найдена путем подстановки этого дохода в общую формулу квадратной функции полезности. В результате получим:
 ,
,
где
 - общая полезность
- общая полезность 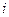 -го дохода (
-го дохода ( 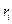 ) портфеля.
) портфеля.
Ожидаемая полезность портфеля может быть найдена из расчета средневзвешенной полезности, получаемой от каждого возможного дохода с использованием в качестве весов вероятностей этих доходов.
 ,
,
где
 - ожидаемая полезность портфеля.
- ожидаемая полезность портфеля.
Выполнив умножение в последнем выражении, получим:
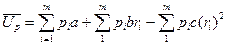 .
.
Первый член в правой части равен  , так как сумма вероятностей всех возможных доходов равна 1.
, так как сумма вероятностей всех возможных доходов равна 1.
Второй член в правой части представляет собой ожидаемый доход портфеля, умноженный на  .
.
Значение третьего члена в правой части уравнения не очевидно.
Запишем каждый входящий в третий член доход в виде суммы ожидаемого дохода портфеля и разницы между ним и отдельно рассматриваемым доходом, то есть каждый 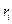 может быть выражен как
может быть выражен как  .
.
Используя такие обозначения, третий член может быть записан в виде:
 .
.
Перемножив выражение в скобках, получим:

Первый член этого выражения после умножения становится равным 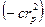 .
.
Можно также показать, что последний член равен нулю.
Второй элемент после умножения на  будет представлять дисперсию дохода портфеля.
будет представлять дисперсию дохода портфеля.
Таким образом, последнее выражение может быть переписано:
 .
.
Наконец, выражение ожидаемой полезности портфеля может быть представлено следующим образом:
 .
.
Вывод формулы риска инвестиционного портфеля для ценных бумаг двух типов
Основное определение дисперсии распределения вероятностей случайной переменной ( 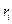 ) имеет вид:
) имеет вид:
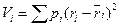 .
.
где
а) 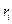 - один из возможных доходов от
- один из возможных доходов от  - й ценной бумаги:
- й ценной бумаги:
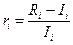 ,
,
где 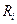 - прогноз будущей стоимости ценной бумаги в конце определенного периода плюс дивиденды;
- прогноз будущей стоимости ценной бумаги в конце определенного периода плюс дивиденды;
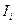 - размер первоначальной инвестиции.
- размер первоначальной инвестиции.
б) 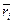 - математическое ожидание дохода от
- математическое ожидание дохода от  - й ценной бумаги
- й ценной бумаги
 ,
,
где 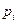 - вероятность
- вероятность 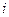 - го дохода от
- го дохода от  - й ценной бумаги
- й ценной бумаги
в)  - дисперсия дохода от
- дисперсия дохода от  - й ценной бумаги
- й ценной бумаги
Поэтому дисперсия портфеля ( 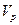 ) может быть записана так:
) может быть записана так:
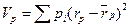 ,
,
где
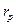 - один из возможных доходов от портфеля ценных бумаг
- один из возможных доходов от портфеля ценных бумаг
Если портфель состоит из двух ценных бумаг (  и
и 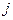 ), а весами являются доли
), а весами являются доли  и
и 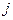 в портфеле (
в портфеле (  и
и  ), тогда
), тогда
 .
.
Путем простых преобразований приходим к:
 ,
,
где
 - ковариация двух случайных величин, доходов
- ковариация двух случайных величин, доходов 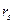 и
и  от двух ценных бумаг
от двух ценных бумаг  и
и 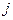 .
.
|
из
5.00
|
Обсуждение в статье: Приложение к модели Г. Марковица |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

