Определение математического ожидания

Математическим ожиданием 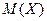дискретной случайной величины называется сумма произведений всех ее возможных значений ( ) на их вероятности ( ):

.

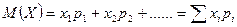Важно отметить свойства математического ожидания:

Из определения математического ожидания дискретной случайной величины непосредственно следует, что:

1. Постоянный множитель можно выносить за знак математического ожидания:

.

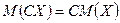Математическое ожидание суммы двух случайных величин равно сумме их математических ожиданий (теорема сложения математических ожиданий):

.

Заметим, что удобство математического ожидания объясняется его следующими свойствами:

1. Математическим ожиданием выборочного значения признака служит как раз среднее арифметическое значение признака в генеральной совокупности (генеральное среднее значение):

2. Математическое ожидание от разницы между случайной величиной и её математическим ожиданием равно 0, то есть . Другими словами, сумма уклонений в положительную сторону равна сумме уклонений в отрицательную сторону

3. Сумма квадратов уклонений (дисперсия) от средней величины меньше, чем сумма квадратов уклонений от всякой другой величины (см. далее свойства дисперсии).

Определение дисперсии

Наряду с характеристиками положения (математическое ожидание показывает центр распределения) большую роль играют характеристики рассеяния.

Рассеяние случайной величины связано с отклонением этой величины от ее центра распределения .

Непосредственное осреднение этого отклонения не может дать числовой характеристики рассеяния, так как

Определения:

Основной характеристикой рассеяния случайной величины служат дисперсия и среднее квадратическое отклонение , определяемое по формуле:

где .

Метод вычисления дисперсии для дискретных случайных величин:

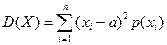
Свойства дисперсии:

,

где (с) - любое число.

Доказательство:

Формула вытекает из линейности математического ожидания:

так как

,

Тогда:

Из последней формулы вытекает, что:

Средний квадрат отклонения случайной величины от ее центра распределения меньше, чем средний квадрат ее отклонения от любого другого числа (с):

В частном случае при с = 0 получаем удобную формулу для вычисления дисперсии :

Теорема:

При линейном преобразовании случайной величины , то есть для линейной функции дисперсия увеличивается в раз, а среднее квадратическое отклонение - в раз.

Например:

Доказательство:

В силу линейности математического ожидания имеем

Поэтому: