 |
Главная |
Теплоемкость твердых тел. Закон Дюлонга и Пти
|
из
5.00
|
Тепловые свойства твердых тел
При любой температуре атомы твердого тела совершают тепловые колебания. При нагреве твердого тела увеличивается колебательная энергия атомов, а при остывании твердого тела атомы излучают энергию. Закономерности поглощения и излучения тепловой энергии характеризуются теплоемкостью.
Молярная теплоемкость численно равна энергии, поглощенной веществом при его нагреве на 1 °С.
 (6.1)
(6.1)
В 1819 г. Дюлонг и Пти экспериментально установили закон, согласно которому удельная теплоемкость всех твердых тел при высоких температурах есть величина постоянная и равная 25 Дж/моль×К, или 3R.
Согласно классической физике, тепловая энергия равномерно распределяется по степеням свободы:  . Каждый атом имеет три степени свободы и характеризуется полной энергией, равной кинетической энергии плюс потенциальная энергия. Для отдельного атома
. Каждый атом имеет три степени свободы и характеризуется полной энергией, равной кинетической энергии плюс потенциальная энергия. Для отдельного атома  . 1 моль вещества содержит NA атомов, тогда его средняя тепловая энергия E = 3NAkT.
. 1 моль вещества содержит NA атомов, тогда его средняя тепловая энергия E = 3NAkT.
Таким образом,
 (6.2)
(6.2)
Однако, при низких температурах закон Дюлонга и Пти не работает (рис. 6.1) и это следует объяснить.

Рис. 6.1. Температурная зависимость теплоемкости твердых тел
Теплоемкость твердых тел.
1. Модель Эйнштейна.
В 1907 г. Эйнштейн, исходя из гипотезы Планка, предложил первую модель, объясняющую низкотемпературный ход теплоемкости. Он предположил:
1) Твердое тело – это совокупность одинаковых гармонических осцилляторов (атомов), которые колеблются независимо друг от друга с одинаковой частотой w в трех взаимно перпендикулярных направлениях.
2) Энергия осцилляторов квантована по Планку  .
.
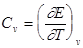 (6.3)
(6.3)
Из (5.44):
 (6.4)
(6.4)
 (6.5)
(6.5)
а) Высокие температуры:  (exp в числителе стремится к 1, в знаменателе exp разложим в ряд). Выполняется закон Дюлонга и Пти:
(exp в числителе стремится к 1, в знаменателе exp разложим в ряд). Выполняется закон Дюлонга и Пти:
 (6.6)
(6.6)
б) Низкие температуры: 
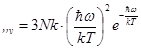 (6.7)
(6.7)
т.е. Cv ® 0 , 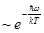 .
.
Причина – неравномерное распределение энергии по степеням свободы, т.е.  .
.
Однако, модель Эйнштейна плохо согласуется с экспериментом (рис. 6.2).

Рис. 6.2. Сравнение расчетов по модели Эйнштейна (2) с экспериментальной зависимостью  (1).
(1).
2. Модель Дебая
Дебай (1912 г.) учел наличие в твердом теле различных мод нормальных колебаний.
Тогда для единичного объема (5.50) через w:


 (6.8)
(6.8)



Характеристическая температура Дебая q определяется через предельную частоту wD, соответствующую предельному значению волнового вектора kD на границе зоны Бриллюэна, когда  т.е. при температуре Дебая возбуждены все возможные собственные колебания кристалла. В фазовом пространстве волновых векторов
т.е. при температуре Дебая возбуждены все возможные собственные колебания кристалла. В фазовом пространстве волновых векторов  значение kD связано с полным числом колебаний N условием:
значение kD связано с полным числом колебаний N условием:
 , (6.9)
, (6.9)
где (2p)3 – объем k-пространства, приходящегося на 1 волновой вектор.
Так как  , в p-пространстве объем равен h3, в k-про-странстве – (2p)3.
, в p-пространстве объем равен h3, в k-про-странстве – (2p)3.
Таким образом, kD = (6p2N)1/3.
а) Высокие температуры: 
ex – 1 » 1 + x – 1 = x
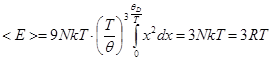 (6.10)
(6.10)
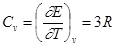 (6.11)
(6.11)
б) Низкие температуры: 
Заменяя пределы интегрирования:

 (6.12)
(6.12)
 (6.13)
(6.13)
Этот результат хорошо согласуется с экспериментом при Т ~ 0 К и лучше, чем модель Эйнштейна при более высоких температурах (рис. 6.2).
Некоторые значения q для полупроводников приведены в таблице 6.1.
Таблица 6.1
| DЕg, эВ | wо×10–13 | qD, К | |
| Si | 1,08 | 9,45 | |
| Ge | 0,66 | 4,8 | |
| GaAs | 1,35 | 5,35 |
В металлах вклад в теплоемкость дают также свободные электроны плюс решетка (у диэлектриков)

|
из
5.00
|
Обсуждение в статье: Теплоемкость твердых тел. Закон Дюлонга и Пти |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

