ПРЕДСТАВЛЕНИЕ АНАЛИТИЧЕСКИХ ФУНКЦИЙ РЯДАМИ

Ряд Тейлора.

Теорема 10. Если функция f(z) аналитична в круге , то она в этом круге может быть представлена рядом Тейлора:

, где - коэффициент ряда разложения.

, где n=0, 1, 2…

В любой замкнутой области, принадлежащей этому открытому кругу, ряд Тейлора сходится равномерно.

Точка а – центр разложения, R – радиус сходимости.

2. Ряд Лорана.

Будем предполагать, что функция f(z) аналитична в кольце К: .

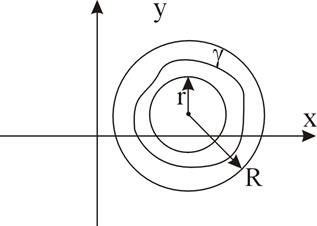Рис. 1

Теорема 11. Если функция f(z) аналитична в кольце К, то она в этом кольце может быть представлена рядом Лорана:

, где

- любой замкнутый контур, лежащий целиком в кольце К и охватывающий точку а, которая является центром разложения.

Ряд Лорана можно получить, расширяя ряд Тейлора в область отрицательных значений n, n <0.

Сумма членов ряда Лорана, содержащих отрицательные степени называются главной частью ряда Лорана. Сумма членов ряда Лорана, содержащих положительные степени называется правильной частью ряда Лорана.

Ряд Лорана (а) сходится в области, в которой сходятся ряды (б) и (в). Пусть ряд Тейлора сходится в круге , ряд (б) сходится вне круга

, тогда если r>R, то ряд Лорана расходится, если r<R, то сходится в кольце К.

Пример.

Рассмотрим разложение функции f(z).

. Выберем в качестве центра разложения точку z=0.

1) Функция f(z) аналитична в круге 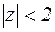. В соответствии с теоремой 10 она может быть представлена рядом Тейлора: .

Рис. 2

2) Функция f(z) аналитична в кольце . По теореме 11 она может быть представлена рядом Лорана:

,

3) Функция f(z) аналитична в кольце . По теореме 11 она может быть представлена рядом Лорана:

,

ОСОБЫЕ ТОЧКИ И ВИД РЯДА ЛОРАНА.

Точка а называется изолированной особой точкой функции f(z), если найдется окрестность точки а, в которой функция f(z) аналитична и аналитичность нарушается при переходе к самой точке.

Более точное определение:

Точка а называется изолированной особой точкой функции f(z), если найдется кольцо К, вида , в котором функция f(z) аналитична и аналитичность не имеет места в самой точке.

Различают три типа изолированных особых точек:

1. изолированная особая точка а называется устранимой, если существует .

Пример.

z=0 – устранимая изолированная особая точка функции 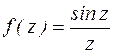, т. к.

Название устранимая особая точка оправдывается тем, что особенность функции в этой точке можно устранить, если положить

2. изолированная особая точка а называется полюсом, если функция f(z) неограниченно возрастает при .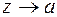

Пример.

z=3 – полюс точка функции .

Каждый полюс а функции f(z) является нулем а функции .

Порядком полюса а функции f(z) называют порядок нуля а функции

Говорят, что точка а является нулем функции порядка m, если .

Пример.

z=3 – полюс третьего порядка функции .

3. изолированная особая точка а называется существенно особой, если не существует .

Пример.

z=0 - существенно особая точка функции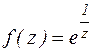

рис. 1

По определению изолированной особой точки существует кольцо

К: , в котором функция f(z) аналитична. Разложим функцию f(z) в этом кольце в ряд Лорана:

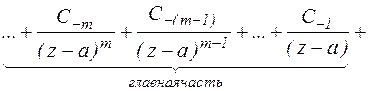
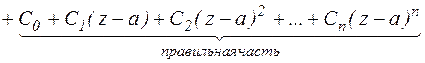
Сумма членов ряда Лорана, содержащих отрицательные степени называются главной частью ряда Лорана. Сумма членов ряда Лорана, содержащих положительные степени называется правильной частью ряда Лорана.

Могут иметь место три случая:

1) ряд Лорана содержит только правильную часть

Тогда , т. е. точка а –устранимая особая точка.

2) ряд Лорана содержит конечную главную часть

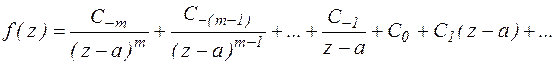
Представим:

Можно видеть, что

Точка а – является полюсом функции f(z). В ТФКП, доказывается, что порядок полюса совпадает с числом членов в главной части ряда Лорана.

3) ряд Лорана содержит бесконечную главную часть

В ТФКП, доказывается, что точка а– является существенно особой точкой функции f(z).

Пусть точка а –изолированная особая точка функции f(z). По определению существует кольцо К: , в котором функция f(z) аналитична. Разложим функцию f(z) в этом кольце в ряд Лорана по степеням . В этом разложении особую роль играет коэффициент ,(коэффициент при сомножителе ), который называется вычетом функции f(z) в точке z=a и обозначается Res

ЛЕКЦИЯ 8

План лекции

1. Теорема о вычетах.

2. Основные формулы вычета в полюсе.

3. Примеры на применение теоремы о вычетах.

ТЕОРЕМА О ВЫЧЕТАХ.

Пусть точка а –изолированная особая точка функции f(z). По определению существует кольцо К: , в котором функция f(z) аналитична. Разложим функцию f(z) в этом кольце в ряд Лорана: (1)

Обозначим замкнутый контур целиком лежащий в кольце К и охватывает точку а. Вычислим интеграл:

Рассмотрим интеграл . Выделим три случая:

1) 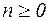, (по теореме 7)

2) , 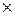Res .

3) 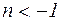, (по формуле Коши для высших производных)

Пояснение: формула Коши для высших производных

Заменим в формуле Коши 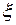на z, z на а

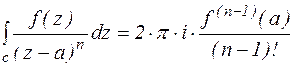
Получили равенство: Res (2)

Теорема 12.(теорема о вычетах) Если функция f(z) аналитична в односвязной области D за исключением конечного числа изолированных особых точек и непрерывна на границе c одласти D, то

Res

Доказательство:

Выделим особые точки из области D с помощью замкнутых контуров . Контура выбираются таким образом, чтобы они не пересекались друг с другом и контуром с.

Рис. 1

Получим (n+1) связанную область, ограниченную с и (к=1, 2,…n), в которых функция f(z) аналитична. По теореме 9: 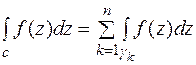(3).

В соответствии с равенством (2): Res (4)

Подставляя (4) в (3), получим: Res .

ОСНОВНЫЕ ФОРМУЛЫ ВЫЧЕТОВ В ПОЛЮСЕ.

1. Найдем вычет Res , полагая, что функция f(z) аналитична в точке а. Обозначим через с замкнутый контур, целиком лежащий в области аналитичности функции f(z) и охватывающий точку а. По теореме о вычетах:

Res

По формуле Коши:

Из сравнения полученных результатов следует Res

2. Найдем Res 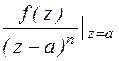, полагая, что функция f(z) аналитична в точке а. По теореме о вычетах: Res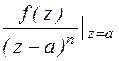

С другой стороны по формуле Коши для производных:

Из сравнения полученных формул следует

Res

3. Общая формула вычета в полюсе первого порядка.

Пусть а – полюс первого порядка функции f(z). По определению существует кольцо К: , в котором функция f(z) аналитична. Разложим функцию f(z) в этом кольце в ряд Лорана:

Перейдем к пределу при 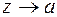в последнем выражении:

Res

Res

4. Найдем Res 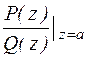, полагая, что

При выписанных условиях точка а является полюсом первого порядка функции . Воспользуемся полученным в предыдущем пункте выражением.

Res

. Получим формулу

Res при

5. Общая формула вычета в полюсе порядка m.

Пусть а – полюс порядка m функции f(z). Выпишем соответствующий этому полюсу ряд Лорана:

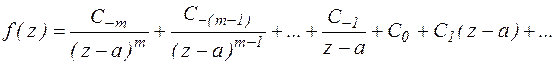
Продифференцируем последнее выражение (m-1) раз

Перейдем к пределу

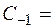Res

Получим следующие формулы вычетов в полюсе

Res

Res

Res ,

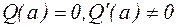
Res (Общая формула вычета в полюсе первого порядка)

Res (Общая формула вычета в полюсе порядка m)

Пример 1.

, с:

рис. 1

(3 формула вычета)

Пример 2.

, с: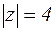

рис. 2

- являются полюсами первого порядка.

Правило определения порядка полюса: нужно из порядка нуля знаменателя вычесть порядок нуля числителя.

Аналогичным образом легко показать, что , поэтому

 

ЛЕКЦИЯ 9

План лекции

1. Лемма Жордана.

2. 2, 3 и 4-ая формулировки леммы Жордана.

3. Применение леммы Жордана для вычисления несобственных интегралов.

 

 

ЛЕММА ЖОРДАНА.

Лемма Жордана (первая формулировка): Если на некоторой последовательности дуг , ( 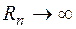при , а фиксировано) функция равномерно относительно аргумента z, то для любого .

Рис. 1

Положим , тогда дуги примут вид: ,

, ,

, ,

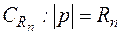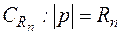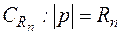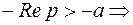
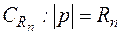Функциональный множитель . Другие изменения, которые вызваны заменой учтем, переходом от функции g(z) к функции F(p).

Лемма Жордана (вторая формулировка): Если на некоторой последовательности дуг 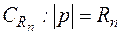, ( 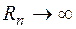, а фиксировано) функция равномерно относительно аргумента р, то для любого .

Рис. 2

Заменим во второй формулировке леммы Жордана р на –р. В этом случае контур 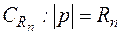, 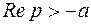. В функциональном многочлене 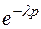знак минус введем в параметр 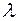, т. е. .

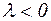Лемма Жордана (третья формулировка): Если на некоторой последовательности дуг 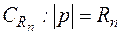, 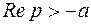( 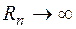, а фиксировано) функция равномерно относительно аргумента р, то для любого .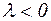

 

 

Рис. 3

Заменим в первой формулировке z на –z. В функциональном множителе знак минус введем в параметр 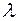, т. е. 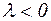. Контур принимает вид , .

Лемма Жордана (четвертая формулировка): Если на некоторой последовательности дуг , ( 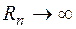, а фиксировано) функция равномерно относительно аргумента z, то для любого .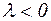

Рис. 4

Пример.

Требуется найти функцию f(z), если преобразование Фурье функции , .

В соответствии с преобразованием Фурье: . Для вычисления данного интеграла можно использовать теорию вычетов и лемму Жордана.

Рассмотрим функцию , положив z=w+iy.

1. Пусть t>0. Рассмотрим замкнутый контур

Рис. 5

Вычислим интеграл

(*)

Перейдем в (*) к пределу при , тогда (по первой формулировке леммы Жордана).

В результате получим, что .

2. Пусть t<0. Рассмотрим замкнутый контур .

Рис. 6

 

Вычислим интеграл по контуру с:

(**)

Перейдем в (**) к пределу при , тогда ( по четвертой формулировке леммы Жордана).

В результате получим, что .

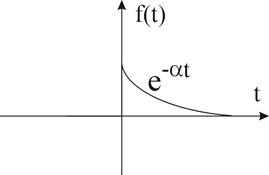
Рис. 7

ИНТЕГРАЛ ФУРЬЕ.

ПРЕОБРАЗОВАНИЕ ФУРЬЕ.

Теорема. Если f(t) кусочно – непрерывная кусочно – дифференцируемая функция и удовлетворяет условиям абсолютной интегрируемости, т. е.

, то функция f(t) представляется интегралом Фурье:

(1)

На практике обычно используют комплексную форму интеграла Фурье:

(2)

 

Покажем, что ряд (1) и (2) эквивалентны

Обозначим

Ясно, что - четная функция , а функция - нечетная функция . Поэтому

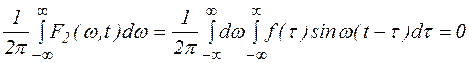в силу нечетности функции.

Окончательно получим, что

Представим интеграл (2) в виде .

Обозначим (3)

тогда (4)

Равенство (4) прямое преобразование Фурье. Оно позволяет вещественной функции f(t) поставить в соответствие функцию F(iw). Обычно прямое преобразование Фурье записывают в виде . Равенство (4) задает обратное преобразование Фурье. Оно позволяет по комплексной функции F(iw) восстановить вещественную функцию f(t).

Преобразования Фурье относятся к интегральным преобразованиям. Переход от вещественной функции f(t) к комплексной функции F(iw) позволяет упростить некоторые математические операции, например, дифференцирование вещественной функции f(t) в комплексной области (для функции F(iw) это соответствует умножению на iw).

Символически прямое преобразование Фурье представляется в виде:

, а обратное .

Рассмотрим физический смысл интеграла (4). Множитель задает гармоническую функцию. По определению интеграл представляет собой операцию суммирования по частоте w . Таким образом, из равенства (4) следует, что периодическую функцию можно представить в виде бесконечной суммы гармонических функций, при этом в отличии от ряда Фурье частота w в (4) изменяется непрерывно от до . По аналогии с рядом Фурье функцию F(iw) называют комплексный спектр (спектральная характеристика, спектральная плотность).
ЛЕКЦИЯ 9

План лекции

4. Лемма Жордана.

5. 2, 3 и 4-ая формулировки леммы Жордана.

6. Применение леммы Жордана для вычисления несобственных интегралов.

 

 

ЛЕММА ЖОРДАНА.

Лемма Жордана (первая формулировка): Если на некоторой последовательности дуг , ( 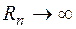при , а фиксировано) функция равномерно относительно аргумента z, то для любого .

Рис. 1

Положим , тогда дуги примут вид: ,

, ,

, ,

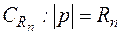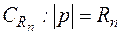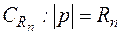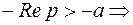
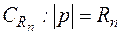Функциональный множитель . Другие изменения, которые вызваны заменой учтем, переходом от функции g(z) к функции F(p).

Лемма Жордана (вторая формулировка): Если на некоторой последовательности дуг 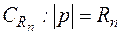, ( 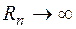, а фиксировано) функция равномерно относительно аргумента р, то для любого .

Рис. 2

Заменим во второй формулировке леммы Жордана р на –р. В этом случае контур 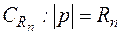, 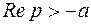. В функциональном многочлене 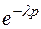знак минус введем в параметр 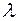, т. е. .

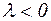Лемма Жордана (третья формулировка): Если на некоторой последовательности дуг 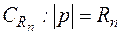, 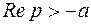( 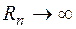, а фиксировано) функция равномерно относительно аргумента р, то для любого .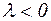

 

 

Рис. 3

Заменим в первой формулировке z на –z. В функциональном множителе знак минус введем в параметр 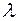, т. е. 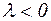. Контур принимает вид , .

Лемма Жордана (четвертая формулировка): Если на некоторой последовательности дуг , ( 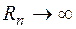, а фиксировано) функция равномерно относительно аргумента z, то для любого .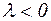

Рис. 4

Пример.

Требуется найти функцию f(z), если преобразование Фурье функции , .

В соответствии с преобразованием Фурье: . Для вычисления данного интеграла можно использовать теорию вычетов и лемму Жордана.

Рассмотрим функцию , положив z=w+iy.

2. Пусть t>0. Рассмотрим замкнутый контур

Рис. 5

Вычислим интеграл

(*)

Перейдем в (*) к пределу при , тогда (по первой формулировке леммы Жордана).

В результате получим, что .

2. Пусть t<0. Рассмотрим замкнутый контур .

Рис. 6

 

Вычислим интеграл по контуру с:

(**)

Перейдем в (**) к пределу при , тогда ( по четвертой формулировке леммы Жордана).

В результате получим, что .

Рис. 7

ИНТЕГРАЛ ФУРЬЕ.

ПРЕОБРАЗОВАНИЕ ФУРЬЕ.

Теорема. Если f(t) кусочно – непрерывная кусочно – дифференцируемая функция и удовлетворяет условиям абсолютной интегрируемости, т. е.

, то функция f(t) представляется интегралом Фурье:

(1)

На практике обычно используют комплексную форму интеграла Фурье:

(2)

 

Покажем, что ряд (1) и (2) эквивалентны

Обозначим

Ясно, что - четная функция , а функция - нечетная функция . Поэтому

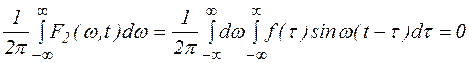в силу нечетности функции.

Окончательно получим, что

Представим интеграл (2) в виде .

Обозначим (3)

тогда (4)

Равенство (4) прямое преобразование Фурье. Оно позволяет вещественной функции f(t) поставить в соответствие функцию F(iw). Обычно прямое преобразование Фурье записывают в виде . Равенство (4) задает обратное преобразование Фурье. Оно позволяет по комплексной функции F(iw) восстановить вещественную функцию f(t).

Преобразования Фурье относятся к интегральным преобразованиям. Переход от вещественной функции f(t) к комплексной функции F(iw) позволяет упростить некоторые математические операции, например, дифференцирование вещественной функции f(t) в комплексной области (для функции F(iw) это соответствует умножению на iw).

Символически прямое преобразование Фурье представляется в виде:

, а обратное .

Рассмотрим физический смысл интеграла (4). Множитель задает гармоническую функцию. По определению интеграл представляет собой операцию суммирования по частоте w . Таким образом, из равенства (4) следует, что периодическую функцию можно представить в виде бесконечной суммы гармонических функций, при этом в отличии от ряда Фурье частота w в (4) изменяется непрерывно от до . По аналогии с рядом Фурье функцию F(iw) называют комплексный спектр (спектральная характеристика, спектральная плотность).

ЛЕКЦИЯ 10

План лекции

1. Единичная ступенчатая функция.

2. Дельта - функция.

3.