 |
Главная |
Прогнозирование на основе экстраполяции предполагает, что найденная закономерность развития внутри динамического ряда сохраняется и вне этого ряда
|
из
5.00
|
При составлении прогнозов социально-экономических явлений обычно оперируют интервальной оценкой, т.е. рассчитывают так называемые доверительные интервалы прогноза с заданной вероятностью.
Границы интервалов определяются по формуле:
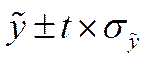 ,
,
где 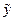 - точечный прогноз, рассчитанный по модели;
- точечный прогноз, рассчитанный по модели; 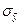 - ошибка прогноза (среднее квадратическое отклонение фактических уровней от расчетных по модели); t – коэффициент доверия по распределению Стъюдента.
- ошибка прогноза (среднее квадратическое отклонение фактических уровней от расчетных по модели); t – коэффициент доверия по распределению Стъюдента.
Построив уравнение регрессии, проводят оценку его надежности. Это делается посредством критерия Фишера (F). Фактический уровень (Fфакт) сравнивается с теоретическим (табличным) значением:
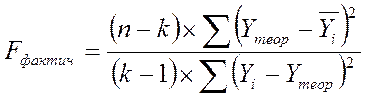
где k - число параметров функции, описывающей тенденцию; n - число уровней ряда;
Fфакт сравнивается с Fтеор (по таблицам) при v1 = (k - 1 ), v2 = (n - k) степенях свободы и уровне значимости a (обычно a = 0,05). Если Fфакт > Fтеор, то уравнение регрессии значимо, т. е. построенная модель адекватна фактической временной тенденции.
Для аппроксимации процесса изменения во времени используют несколько моделей, а наилучшую пригодность проверяют на основе принципа минимизации квадратов отклонений фактических и выравненных (теоретических) значений динамического ряда.
Также критерием выбора модели является средняя ошибка аппроксимации
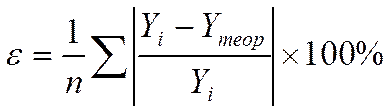
Все эти характеристики имеют один и тот же смысл: показывают как близко аналитическая функция выравнивания огибает все значения исходного ряда.
Методика аналитического выравнивания динамических рядов
Графическое изображение фактических эмпирических данных, характеризующих динамику изучаемого социально-экономического явления или процесса
Анализ формы распределения эмпирических данных динамического ряда
Предположение (гипотеза) о возможности описания фактических данных линейным или нелинейным уравнением регрессии
Определение неизвестных параметров (коэффициентов) уравнений на основе МНК (метода наименьших квадратов) по фактическим данным
Построение аналитической зависимости в виде уравнения регрессии (математической модели), теоретически описывающей эмпирические данные динамического ряда
Интерпретация полученного уравнения (его коэффициентов и их знаков) с точки зрения их экономического содержания
Определение теоретических (выравненных по полученной модели) уровней динамического ряда для сопоставления их с фактическими уровнями ряда
Проверка адекватности модели на основе F-критерия Фишера и расчета ошибки аппроксимации, определение расхождения между теоретическими и фактическими данными
|
из
5.00
|
Обсуждение в статье: Прогнозирование на основе экстраполяции предполагает, что найденная закономерность развития внутри динамического ряда сохраняется и вне этого ряда |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

