 |
Главная |
Тема 5: «Дифференциальные уравнения»
|
из
5.00
|
Пример 5.1. Найти общее решение или общий интеграл дифференциального уравнения:

Данное уравнение является однородным уравнением 








Разделяя переменные, получим:






 Общее решение
Общее решение
Пример 5.2. Найти частное решение дифференциального уравнения  удовлетворяющего начальным условиям
удовлетворяющего начальным условиям 

Найдем общее решение однородного уравнения
 .
.
Составляем характеристическое уравнение
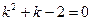 .
.

Полученное квадратное уравнение имеет действительные различные корни: k1=1 k2=-2. Следовательно, общее решение однородного линейного дифференциального уравнения имеет вид
 .
.







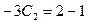




Пример 5.3. Найти общее решение или общий интеграл дифференциального уравнения
 ,
,
Решение. Данное уравнение является уравнением с разделяющимися переменными.
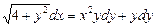


Разделяя переменные, получим

 .
.

Интегрируя обе части равенства: 


Пример 5.4. Найти общее решение или общий интеграл дифференциального уравнения  ,
,
Данное уравнение является однородным дифференциальным уравнением
Сделаем подстановку  . Тогда y=ux и y'=u'x+u.
. Тогда y=ux и y'=u'x+u.













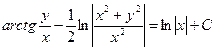



Это и есть общий интеграл исходного дифференциального уравнения.
Пример 5.5. Найти общее решение или общий интеграл дифференциального уравнения 
Данное уравнение является линейным дифференциальным уравнением.
Сделаем подстановку y=uv; тогда y'=u'v+uv'.
Тогда данное уравнение примет вид


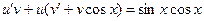






















Пример 5.6. Найти общее решение или общий интеграл дифференциального уравнения 

 Данное уравнение является дифференциальным уравнением Бернулли.
Данное уравнение является дифференциальным уравнением Бернулли.
Сделаем подстановку y=uv; тогда y'=u'v+uv'.
Тогда данное уравнение примет вид







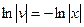












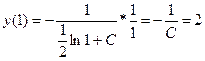



Пример 5.7. Найти общее решение или общий интеграл дифференциального уравнения  ,
,
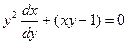




Данное уравнение является линейным дифференциальным уравнением.
Сделаем подстановку х=uv; тогда х'=u'v+uv'.









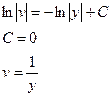
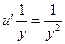












Пример 5.8. Найти общее решение или общий интеграл дифференциального уравнения  .
.










Пример 5.9. Найти общий интеграл (решение) дифференциального уравнения, допускающего понижения порядка: 
Решение.
Данное дифференциальное уравнение не содержит в явном виде искомую функцию y(x), следовательно, оно допускает понижение порядка. Для этого положим y''=p(x) Тогда y'''=dp/dx
и уравнение примет вид

Разделяя переменные, получим 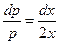












Пример 5.10. Найти частный интеграл (решение) дифференциального уравнения, допускающего понижения порядка: 
Это дифференциальное уравнение не содержит в явном виде независимой переменной x, следовательно, оно допускает понижение порядка. Положим y'=p(y), тогда
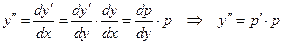 .
.
В результате, исходное уравнение примет вид 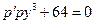



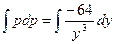


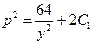








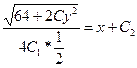

Пример 5.11. Найти частное решение однородного линейного дифференциального уравнения второго порядка:

Составляем характеристическое уравнение
 .
.


Полученное квадратное уравнение имеет действительные корни: k1=0, k2=4. Следовательно, общее решение однородного линейного дифференциального уравнения имеет вид
 .
.
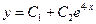
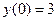
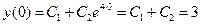
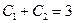

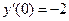





Пример 5.12. Найти частное решение однородного линейного дифференциального уравнения второго порядка: 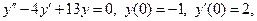
Составляем характеристическое уравнение  .
.
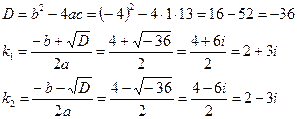
Полученное квадратное уравнение имеет комплексные корни: k1=2+3i, k2=2-3i.


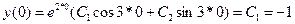






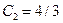

Пример 5.13. Найти частное решение однородного линейного дифференциального уравнения второго порядка: 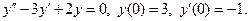
 однородное дифференциальное уравнение второго порядка.
однородное дифференциальное уравнение второго порядка.
 соответствующее характеристическое уравнение
соответствующее характеристическое уравнение

корни действительные и различные


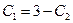


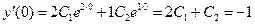


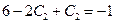



Пример 5.14. Найти общее решение неоднородного линейного дифференциального уравнения второго порядка: 
Найдем сначала общее решение соответствующего однородного уравнения
 .
.
Составляем характеристическое уравнение
 .
.

Полученное квадратное уравнение имеет действительные корни: k1=6, k2=6. Следовательно, общее решение однородного линейного дифференциального уравнения имеет вид
 .
.
Найдем теперь частное решение  неоднородного уравнения. Оно будет иметь такой же вид, как и правая часть неоднородного уравнения: f(x)
неоднородного уравнения. Оно будет иметь такой же вид, как и правая часть неоднородного уравнения: f(x)  , т.е. решение будем искать в виде
, т.е. решение будем искать в виде  k1=k2=6=а, кратность корня = 2
k1=k2=6=а, кратность корня = 2

.
Находя производные этой функции
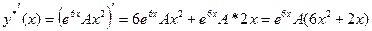


и подставляя их в исходное уравнение, получим




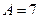
Следовательно, частное решение неоднородного уравнения имеет вид
 .
.
Таким образом, общее решение исходного уравнения имеет вид

Пример 5.15. Найти общее решение неоднородного линейного дифференциального уравнения второго порядка: 
Найдем сначала общее решение соответствующего однородного уравнения
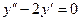 .
.
Составляем характеристическое уравнение
 .
.


Полученное квадратное уравнение имеет действительные корни: k1=0, k2=2. Следовательно, общее решение однородного линейного дифференциального уравнения имеет вид
 .
.

Найдем теперь частное решение  неоднородного уравнения. Оно будет иметь такой же вид, как и правая часть неоднородного уравнения: f(x)
неоднородного уравнения. Оно будет иметь такой же вид, как и правая часть неоднородного уравнения: f(x)  , т.е. решение будем искать в виде
, т.е. решение будем искать в виде  k1=0=а однократный корень характеристического уравнения
k1=0=а однократный корень характеристического уравнения

 .
.
Находя производные этой функции


и подставляя их в исходное уравнение, получим




Найдем неизвестные коэффициенты A, B, C. Для этого сравним коэффициенты при одинаковых степенях x:

Следовательно, частное решение неоднородного уравнения имеет вид

Таким образом, общее решение исходного уравнения имеет вид

Пример 5.16. Найти общее решение неоднородного линейного дифференциального уравнения второго порядка: 
Найдем сначала общее решение соответствующего однородного уравнения
 .
.
Составляем характеристическое уравнение  .
.
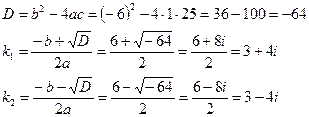
Полученное квадратное уравнение имеет комплексные корни: k1=3+4i, k2=3–4i.

Найдем теперь частное решение неоднородного уравнения.
Оно будет иметь такой же вид, как и правая часть неоднородного уравнения: 
а=0+4i не является корнем характеристического уравнения
Следовательно, общее решение однородного линейного дифференциального уравнения имеет вид 


и подставляя их в исходное уравнение, получим
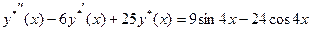








Следовательно, частное решение неоднородного уравнения имеет вид

Таким образом, общее решение исходного уравнения имеет вид

Пример 5.18. Найти общее решение неоднородного линейного дифференциального уравнения второго порядка:  Найдем сначала общее решение соответствующего однородного уравнения
Найдем сначала общее решение соответствующего однородного уравнения  .
.
Составляем характеристическое уравнение  .
.


Полученное квадратное уравнение имеет действительные корни: k1=0, k2=-2. Следовательно, общее решение однородного линейного дифференциального уравнения имеет вид
 .
.

Найдем теперь частное решение  неоднородного уравнения. Оно будет иметь такой же вид, как и правая часть неоднородного уравнения:
неоднородного уравнения. Оно будет иметь такой же вид, как и правая часть неоднородного уравнения:

 .
.

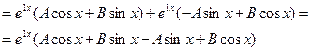


 и подставляя их в исходное уравнение, получим
и подставляя их в исходное уравнение, получим


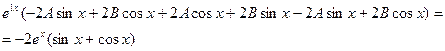


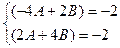

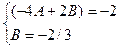

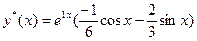

Пример 5.19. Найти общее решение неоднородного линейного дифференциального уравнения второго порядка: Найти общее решение линейного дифференциального уравнения методом вариации постоянных (методом Лагранжа):
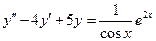 .
.
Найдем сначала общее решение соответствующего однородного уравнения
 .
.
Составляем характеристическое уравнение
 .
.
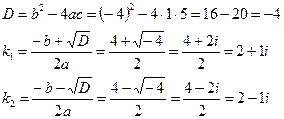
 Общее решение однородного уравнения
Общее решение однородного уравнения
Найдем частное решение неоднородного уравнения
Рассмотрим правую часть исходного уравнения

Решим задание через вронскиан

Так как  , то выражения принимают значения
, то выражения принимают значения


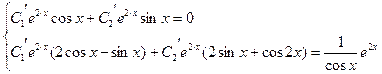




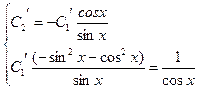

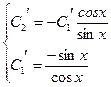



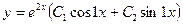

Пример 5.20. Найти решение системы дифференциальных уравнений:

Решение:




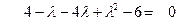
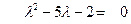










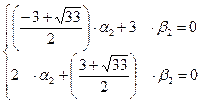







Пример 5.21. Найти решение системы дифференциальных уравнений: 







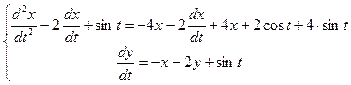

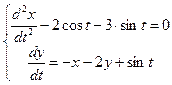









Ответ:
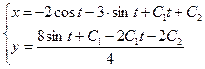
Пример 5.22.
Найти функцию дохода  , если известно, что величина потребления задаётся функцией
, если известно, что величина потребления задаётся функцией  , коэффициент капиталоёмкости прироста дохода
, коэффициент капиталоёмкости прироста дохода  ,
,  .
.
| № задачи | 
| 
| 
|
| C=3t | 0,4 |
Найти функцию дохода  , если известно, что величина потребления задаётся функцией
, если известно, что величина потребления задаётся функцией 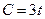 , коэффициент капиталоёмкости прироста дохода
, коэффициент капиталоёмкости прироста дохода  ,
, 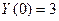 .
.
Решение:
Известно, что функция дохода равна
 ,
,
где  – сумма инвестиций,
– сумма инвестиций,  – величина потребления.
– величина потребления.
А также имеет место дифференциальное уравнение
 ,
,
где  – коэффициент капиталоёмкости прироста дохода. По условию задачи составим дифференциальное уравнение:
– коэффициент капиталоёмкости прироста дохода. По условию задачи составим дифференциальное уравнение:
 , или
, или 

Итак, функция дохода удовлетворяет линейному неоднородному уравнению первого порядка. Будем искать его решение в виде  .
.
Тогда  , подставим в уравнение
, подставим в уравнение 
1)  2)
2) 



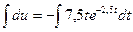




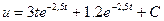
Общее решение  или
или 
Используя начальные условия 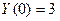 , найдём
, найдём 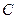 :
: 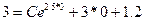
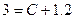 или
или  .
.
Итак, функция дохода имеет вид  .
.
Задания к теме 5 «Дифференциальные уравнения»
Проинтегрировать данные уравнения или системы уравнений; если заданы начальные условия, то выделить частные решения:
1. 
2. 
3. 
4. 
5. 
6. 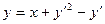 .
.
7. 
8. 
9.  .
.
10. 
11.  .
.
12. 
13.  .
.
14. 
15.  .
.
16. 
17.  .
.
18. 
19.  .
.
20.  ;
;
21.  .
.
22.  .
.
23. 
24. 
25.


