Доверительные интервалы

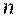– объем выборки, 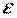– статистическая точность

Нормальным называют распределение вероятностей непрерывной случайной величины, которое задается плотностью .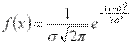
Нормальное распределение задается двумя параметрами: – математическим ожиданием, – средним квадратическим отклонением.
График плотности нормального распределения называют нормальной кривой (кривой Гаусса).
Нормированным называют нормальное распределение с араметрами Плотность нормированного распределения задается формулой .

Вероятность попадания в заданный интервал нормальной случайной величины

Как уже было установлено, вероятность того, что непрерывная случайная величина примет значение, принадлежащее интервалу , равна определенному интегралу от плотности распределения, взятому в соответствующих пределах:

.
Для нормально распределенной случайной величины соответственно получим:
.
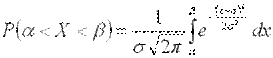Преобразуем последнее выражение, введя новую переменную . Следовательно, показатель степени выражения, стоящего под интегралом преобразуется в:
.
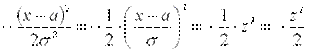Для замены переменной в определенном интеграле еще необходимо заменить дифференциал и пределы интегрирования, предварительно выразив переменную из формулы замены:

;
;
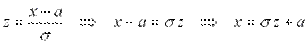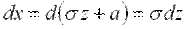– нижний предел интегрирования;

– верхний предел интегрирования;

(для нахождения пределов интегрирования по новой переменной в формулу замены переменной были подставлены и – пределы интегрирования по старой переменной ).

Подставим все в последнюю из формул для нахождения вероятности:

где – функция Лапласа.

Вывод: вероятность того, что нормально распределенная случайная величина Х примет значение, принадлежащее интервалу , равна:
,
где 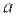– математическое ожидание, – среднее квадратическое отклонение данной случайной величины.

Указания к выполнению практической работы: Данные для решения задач взять из таблицы №2. Работу оформить в отдельных тетрадях для практических работ. При необходимости использовать литературу из приведенного ниже списка.

Задания:

1. Случайная величина Х распределена нормально и σ = 3. Найти доверительный интервал для оценки математического ожидания по выборочным средним, если n = t и задана надежность γ = Р/100.

2. Случайная величина Х имеет нормальное распределение с математическим ожиданием α = 15 и средним квадратическим отклонением σ = 5. Найти вероятность того, что случайная величина Х примет значение, принадлежащее интервалу (b, t).

Практическая работа № 14 «Моделирование ДСВ и НСВ»

Основные понятия и определения.