 |
Главная |
Моделирование непрерывных случайных величин
|
из
5.00
|
При моделировании непрерывных СВ с заданным законом распределения могут использоваться три метода:
- нелинейных преобразований;
- композиций;
- табличный.
Первые два метода требуют от разработчика модели весьма серьезной математической подготовки и в данном пособии не рассматриваются. Третий метод, условно названный «табличным», основан на замене закона распределения непрерывной СВ специальным расчетным соотношением, которое позволяет вычислять значение СВ по значению случайного числа, равномерно распределенного все на том же интервале [0, 1]. Такие соотношения получены практически для всех наиболее распространенных видов распределений и приведены в справочной литературе. В качестве примера ниже приведено расчетное соотношение для показательного закона распределения показательного:
 (*), где
(*), где  – параметр показательного распределения, r – равномерно распределённое СЧ.
– параметр показательного распределения, r – равномерно распределённое СЧ.
Технологию моделирования непрерывных случайных величин поясним на примере.
Специалисты в области надежности технических систем доказали, что интервалы времени между отказами распределены по экспоненциальному закону. Чтобы получить в модели величину промежутка времени между двумя соседними отказами, достаточно сгенерировать случайное число r и подставить его в выражение (*); разумеется, при этом должен быть известен параметр распределения  .
.
В одной и той же имитационной модели могут фигурировать различные случайные факторы, одни могут быть представлены как случайные события, другие – как случайные величины; более того, если моделируется поведение достаточно сложной системы, то ее функционирование может быть связано с возникновением нескольких типов событий и учетом большого числа случайных величин, распределенных по различным законам. Если же моделирование всех случайных факторов основано на использовании одного датчика, генерирующего одну «общую» последовательность случайных чисел, то с математической точки зрения их нельзя считать независимыми. В связи с этим для моделирования каждого случайного фактора стараются использовать отдельный генератор, или, по крайней мере, обеспечивать создание новой последовательности случайных чисел. Во многих специализированных языках и пакетах моделирования такая возможность предусмотрена.
Указания к выполнению практической работы: Данные для решения задач взять из таблицы №1. Работу оформить в отдельных тетрадях для практических работ. При необходимости использовать литературу из приведенного ниже списка.
Задания:
1. Разыграть Х возможных значений случайной еличины Х распределенной нормально с параметрами M{X} = 0 и σ = 1. Оценить параметры разыгранной случайной величины Х.
2. Смоделировать b значений дискретной случайной величины, заданной таблицей распределения:

Практическая работа № 15 «Получение методами математической статистики результатов»
Основные понятия и определения
Признак – это основная отличительная черта, особенность изучаемого явления или процесса. Количественное представление признака называется показателем.
Результативный признак – исследуемый показатель процесса, характеризующий эффективность процесса.
Факторный признак – показатель, влияющий на значение результативного показателя.
Целью регрессионного анализа является оценка функциональной зависимости условного среднего значения результативного признака (Y) от факторных (x1, x2, …, xn), выражаемой в виде уравнения регрессии:
Y = f(x1, x2, …, xn).
Для характеристики связей между признаками используют следующие типы функций:
- линейную  ;
;
- гиперболическую  ;
;
- показательную  ;
;
- параболическую  ;
;
- степенную  .
.
Линейная функция используется в случае, если результативный и факторный признаки возрастают одинаково, примерно в арифметической прогрессии, гиперболическая – если связь между Y и x, наоборот, обратная. Параболическая или степенная функция применяются, если факторный признак увеличивается в арифметической прогрессии, а результативный значительно быстрее.
Линейная однофакторная регрессия:  . Для нахождения параметров a0 и а1 используют метод наименьших квадратов. Сущность метода заключается в нахождении параметров a0 и а1, при которых минимизируется сумма квадратов отклонений эмпирических значений результативного признака от теоретических, полученных по выбранному уравнению регрессии. Величину параметров a0 и а1 находим как решение системы нормальных уравнений:
. Для нахождения параметров a0 и а1 используют метод наименьших квадратов. Сущность метода заключается в нахождении параметров a0 и а1, при которых минимизируется сумма квадратов отклонений эмпирических значений результативного признака от теоретических, полученных по выбранному уравнению регрессии. Величину параметров a0 и а1 находим как решение системы нормальных уравнений:
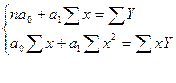 , где n – объём исследуемой совокупности.
, где n – объём исследуемой совокупности.
В уравнении регрессии свободный член регрессии коэффициент a0 показывает совокупное влияние на результативный признак неучтённых (не выделенных для исследования) факторов; его вклад в значение результирующего показателя не зависит от изменения факторов; параметр а1 – коэффициент регрессии – показывает, на сколько изменяется в среднем значение результативного признака при увеличении факторного на единицу собственного измерения.
Пример.По следующим данным, полагая, что зависимость между x и Y линейная, определить значения коэффициентов a0 и а1:
| х | |||||||
| Y |
Решение.Для определения величин a0 и а1 необходимо вычислить следующие значения: åх, åY, åxY, åх2. Расчёты рекомендуется проводить в Excel и оформлять в виде таблицы:
| № п/п | х | Y | х2 | xY | 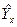
|
| 2,07 | |||||
| 5,92 | |||||
| 9,77 | |||||
| 14,91 | |||||
| 20,05 | |||||
| 22,61 | |||||
| 29,03 | |||||
| Итого | 104,36 |
Система нормальных уравнений имеет вид:

Решив данную систему методом Гаусса, получаем значения: a0=0,876, а1=1,284. Следовательно, 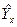 =0,876+1,284х. Т.к. а1>0, связь между признаками прямая (в случае обратной связи коэффициент регрессии отрицательный). При увеличении х на единицу,
=0,876+1,284х. Т.к. а1>0, связь между признаками прямая (в случае обратной связи коэффициент регрессии отрицательный). При увеличении х на единицу, 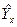 - увеличивается на 1,284. Линейную модель удобно представлять графически:
- увеличивается на 1,284. Линейную модель удобно представлять графически:

Однофакторная параболическая модель второй степени - параболическая регрессия применяется, если факторный признак увеличивается в арифметической прогрессии, а результативный значительно быстрее. В этом случае уравнение регрессии будет иметь вид:
 ;
;
В данном случае задача сводится к определению неизвестных параметров: а0, а1,. Величину параметров a0, а1 и а2 находим как решение системы нормальных уравнений:
 ,
,
Пример.По следующим данным, полагая, что зависимость между x и Y параболическая, определить значения коэффициентов a0, а1 и а2:
| х | ||||||||||
| Y |
Решение.Для определения величин a0, а1 и а2 необходимо вычислить следующие значения: åх, åY, åxY, åх2, åх3, åx4, åх2Y. Расчёты рекомендуется проводить в Excel и оформлять в виде таблицы:
| № п/п | х | Y | xY | х2 | х2Y | х3 | x4 | 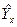
| D= Y - 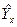
|
| 2,098 | -1,098 | ||||||||
| 3,488 | -0,488 | ||||||||
| 4,903 | 1,097 | ||||||||
| 6,344 | 0,656 | ||||||||
| 7,809 | 0,191 | ||||||||
| 10,815 | 0,185 | ||||||||
| 15,51 | 0,49 | ||||||||
| 22,13 | -1,13 | ||||||||
| 27,36 | -0,36 | ||||||||
| 38,5 | 0,5 | ||||||||
| Итого |
Система нормальных уравнений имеет вид:

Решив данную систему методом Гаусса, получаем значения: a0=0,734, а1=1,352, а2=0,0126. Следовательно, уравнение регрессии имеет вид: 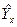 =0,734+1,352х+0,0126х2. Из таблицы видно, что вычисленные по уравнению регрессии значения
=0,734+1,352х+0,0126х2. Из таблицы видно, что вычисленные по уравнению регрессии значения 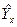 незначительно отличаются от эмпирических данных.
незначительно отличаются от эмпирических данных.
Оценка обратной зависимости между Y и x, может быть дана на основе уравнения гиперболы: 
Величину параметров a0 и а1 находим как решение системы нормальных уравнений:
 ,
,
Пример.По следующим данным, полагая, что зависимость между x и Y выражается уравнением гиперболы, определить значения коэффициентов a0 и а1:
| х | |||||||
| Y |
Решение.Для определения величин a0 и а1 расчёты рекомендуется проводить в Excel и оформлять в виде таблицы:
| № п/п | х | Y | 1/х | Y/х | 1/х2 | 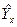
| Di |
| 9,73 | 4,27 | ||||||
| 0,33 | 3,67 | 0,11 | 9,26 | 1,74 | |||
| 0,25 | 2,75 | 0,062 | 9,20 | 1,80 | |||
| 0,67 | 1,5 | 0,028 | 9,13 | -0,13 | |||
| 0,14 | 1,14 | 0,02 | 9,12 | -1,12 | |||
| 0,11 | 0,78 | 0,012 | 9,10 | -2,1 | |||
| 0,10 | 0,5 | 0,01 | 9,09 | -4,09 | |||
| Итого | 2,6 | 24,34 | 1,242 | 64,63 |
Система нормальных уравнений имеет вид:

Решив данную систему методом Гаусса, получаем значения: a0=9,02, а1=0,71. Следовательно, уравнение регрессии имеет вид: 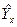 =9,02+0,71/х.
=9,02+0,71/х.
Указания к выполнению практической работы: Работу оформить в отдельных тетрадях для практических работ. При необходимости использовать литературу из приведенного ниже списка.
Задание:
Экспериментальные данные о значениях переменных х и у приведены в таблице.
| i=1 | i=2 | i=3 | i=4 | i=5 | |
| xi | |||||
| yi | 2.1 | 2.4 | 2.6 | 2.8 | 3.0 |
В результате их выравнивания получена функция 
Используя метод наименьших квадратов, аппроксимировать эти данные линейной зависимостью y=ax+b (найти параметры а и b). Выяснить, какая из двух линий лучше (в смысле метода наименьших квадратов) выравнивает экспериментальные данные. Сделать чертеж.
|
из
5.00
|
Обсуждение в статье: Моделирование непрерывных случайных величин |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

