 |
Главная |
ПЕРВЫЙ ТЕСТОВЫЙ МЕТОД ЛЯПУНОВА
|
из
5.00
|
Известно, что с помощью введения переменных состояния  нелинейное дифференциальное уравнение (1.1) можно свести к нелинейному векторному дифференциальному уравнению вида
нелинейное дифференциальное уравнение (1.1) можно свести к нелинейному векторному дифференциальному уравнению вида
 . (1.12)
. (1.12)
Если нелинейность выражается однозначной аналитической функцией, то в рабочей стационарной точке  и вблизи нее первые частные производные
и вблизи нее первые частные производные  ,
, 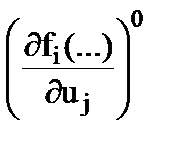 и
и  нелинейных функций
нелинейных функций 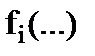 конечны, однозначны и непрерывны. Поэтому нелинейную векторную функцию (1.12) можно линеаризовать, используя первые два члена ряда Тейлора – так называемое «первое приближение». В этом случае, отбрасывая члены выше первого порядка малости, получаем приближенное уравнение линеаризованной модели нелинейной системы в переменных пространства состояний
конечны, однозначны и непрерывны. Поэтому нелинейную векторную функцию (1.12) можно линеаризовать, используя первые два члена ряда Тейлора – так называемое «первое приближение». В этом случае, отбрасывая члены выше первого порядка малости, получаем приближенное уравнение линеаризованной модели нелинейной системы в переменных пространства состояний
 . (1.13)
. (1.13)
Или записывая в иной форме, получим
 , (1.14)
, (1.14)
 , (1.15)
, (1.15)
где элементы матриц A, B и B1 соответственно равны 
 ,
, 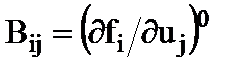 и
и  ; матрица C – матрица выходов.
; матрица C – матрица выходов.
Первая теорема Ляпунова об устойчивости утверждает, что если нелинейная система заменена линейной моделью первого приближения и полученное при этом характеристическое уравнение
 , (1.16)
, (1.16)
векторного дифференциального уравнения
 , (1.17)
, (1.17)
имеет корни  с ненулевыми действительными частями
с ненулевыми действительными частями  , то вопрос об устойчивости решается на основе линейной аппроксимации исходного нелинейного уравнения. В этом случае нелинейности выше первого порядка малости не влияют на устойчивость системы. Если же действительная часть какого-либо корня равна нулю, то данный критерий неприменим к исследуемой системе, так как отброшенные нелинейности влияют на устойчивость и их необходимо учитывать при решении вопроса об устойчивости системы.
, то вопрос об устойчивости решается на основе линейной аппроксимации исходного нелинейного уравнения. В этом случае нелинейности выше первого порядка малости не влияют на устойчивость системы. Если же действительная часть какого-либо корня равна нулю, то данный критерий неприменим к исследуемой системе, так как отброшенные нелинейности влияют на устойчивость и их необходимо учитывать при решении вопроса об устойчивости системы.
В отдельные группы линеаризации можно отнести гармоническую линеаризацию и статистическую.
В дальнейшем будут рассматриваться линейные или линеаризованные детерминированные математические модели ХТП и ХТС с сосредоточенными параметрами. Кроме того, учитывая, что ХТП и ХТС являются сложными системами, то далее будет использоваться термин «динамическая система» - (ДС) как более общее понятие, включающее в себя понятие ХТП и ХТС.
ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ
Пример 2.1
Линеаризовать нелинейные уравнения динамического режима смесителя (рис. 1.1), описывающие изменения уровня L и концентрации Q3A в зоне идеального смешения, полученные на основе уравнений сохранения масс для потоков в целом и для вещества А:
 , (2.1-1)
, (2.1-1)
 , (2.1-2)
, (2.1-2)
 , (2.1-3)
, (2.1-3)
где 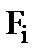 – расход i-го потока, м3/c;
– расход i-го потока, м3/c;  – концентрация вещества А в i-м потоке, кг/кг; L – уровень жидкости в смесителе, м; Ас – площадь поперечного сечения смесителя, м2; s – проходное сечение клапана на сливном трубопроводе, м2; a - коэффициентом расхода жидкости через клапан; g - ускорение свободного падения, м/с2.
– концентрация вещества А в i-м потоке, кг/кг; L – уровень жидкости в смесителе, м; Ас – площадь поперечного сечения смесителя, м2; s – проходное сечение клапана на сливном трубопроводе, м2; a - коэффициентом расхода жидкости через клапан; g - ускорение свободного падения, м/с2.
Решение
Для линеаризации системы уравнений ДС необходимо провести линеаризацию каждого уравнения. Так как данные функции аналитические, то они допускают разложение в ряд Тейлора.
В рассматриваемой математической модели выходными параметрами 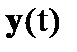 являются Q3A и L, управляющими воздействиями u(t) – s и F2, возмущающими r(t) – F1, Q1A, Q2A.
являются Q3A и L, управляющими воздействиями u(t) – s и F2, возмущающими r(t) – F1, Q1A, Q2A.
Рис. 1.1. Схема смесителя с отводом жидкости самотеком
Полученную нелинейную модель можно линеаризовать в рабочей точке (L0, Q03A) в соответствии с выражением (1.8). Для этого уравнение (2.1-2) преобразуем к виду
 . (2.1-4)
. (2.1-4)
Затем умножим уравнение (2.1-1) на -Q03A и сложим с уравнением (2.1-4), получим
 .
.
(2.1-5)
Уравнения (2.1-1), (2.1-3) и (2.1-5) можно записать в виде уравнения (1.1)
 , (2.1-6)
, (2.1-6)
где
 ,
,
 .
.
.
Линеаризованное уравнение динамики процесса смешения в отклонениях, в соответствии с выражениями (1.8), (1.9) и учетом того, что переменные s и L неразделимы в выражении (2.1-6), можно записать в виде


 . (2.1-7)
. (2.1-7)
Поскольку в рабочей точке выполняются соотношения:
 ,
, 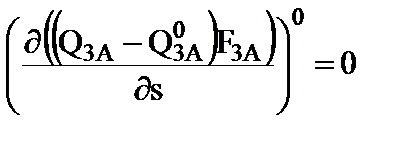 ,
,
 и
и

 ,
,
то оставляя в левой части уравнения (2.1-7) только функции от y(t) и py(t), получим

 .
.
(2.1-8)
Введем относительные величины:

 ,
,  ,
,  ,
,  ,
,
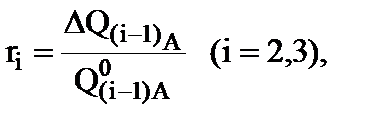

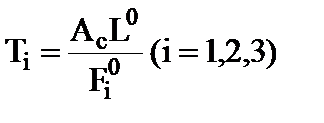
(2.1-9)
и запишем уравнение (2.1-8) в виде
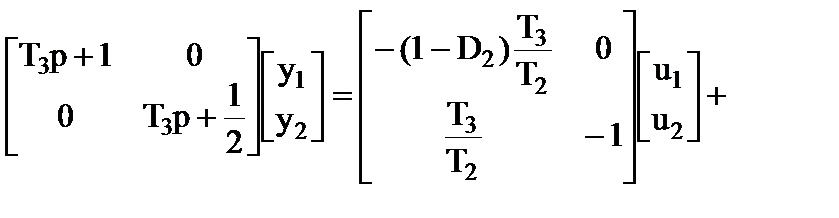
 . (2.1-10)
. (2.1-10)
Матричное дифференциальное уравнение (2.1-10) представляет собой линеаризованную математическую модель смесителя, записанную в символической форме (2.11).
Рассмотрим нелинейную модель изменения уровня жидкости в смесителе – уравнения (2.1-1) и (2.1-3).
Объединяя их, получаем
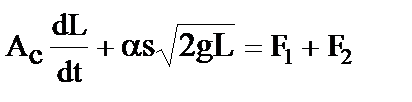 . (2.1-11)
. (2.1-11)
Модель в отклонениях имеет вид
 .
.
(2.1-12)
Для представления модели в относительных величинах, введенных ранее, запишем уравнение (2.1-12) в виде
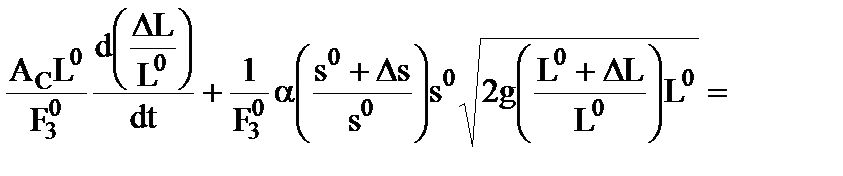
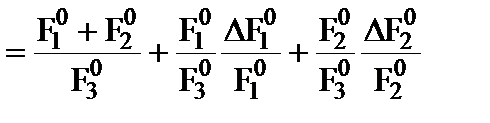 . (2.1-13)
. (2.1-13)
Учитывая, что
 , (2.1-14)
, (2.1-14)
уравнение (2.1-13) принимает вид
 , (2.1-15а)
, (2.1-15а)
или в виде
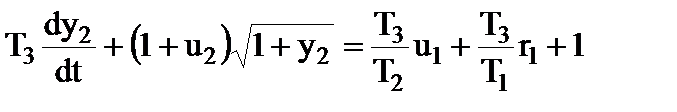 . (2.1-15б)
. (2.1-15б)
Моделирование нелинейного дифференциального уравнения (2.1-15), соотношения (2.1-14) и относительных величин u1, u2, r1, и y2 выполняем в среде MATLAB+Simulink, рис.1.2.
Линеаризованная математическая модели уровня жидкости в смесителе в относительных величинах имеет следующий вид:
 , (2.1-16а)
, (2.1-16а)
или
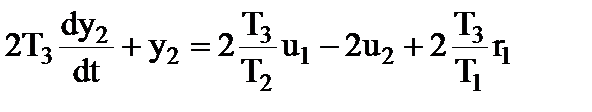 , (2.1-16б)
, (2.1-16б)
т. е. описывается линейным дифференциальным уравнением 1-го порядка. Решение уравнения (2.1-16) при нулевых начальных условиях и ступенчатых воздействиях имеет вид
 .
.
(2.1-17)

Рис. 1.2. Схема моделирования нелинейной математической модели изменения уровня жидкости в смесителе
Схемы моделирования уравнений (2.1-15) и (2.1-16) представлены на рис. 1.3.
Уравнения моделировались при значениях T1=635.8 c, T2=2543.2 c, T3=508.6 c.
Установившиеся значения y2 при u2=0.1 для уравнения (2.1-15) составляет -0.1736, для уравнения (2.1-16) – -0.2, т. е. ошибка линеаризации равна 15.21% (2.64%). Соответственно ошибка при u2=0.05 равна 7.56% (0.7%), а при u2=0.03 – 4.53%. Соответственно u1=0.1 – 1%, r1=0.1 – 3.85%. Из этого следует, что при малых изменениях входных величин (u1=0.1, u2=0.03, r1=0.1) линеаризованная модель достаточно точно описывает процесс изменения уровня жидкости в смесителе (рис. 1.4).
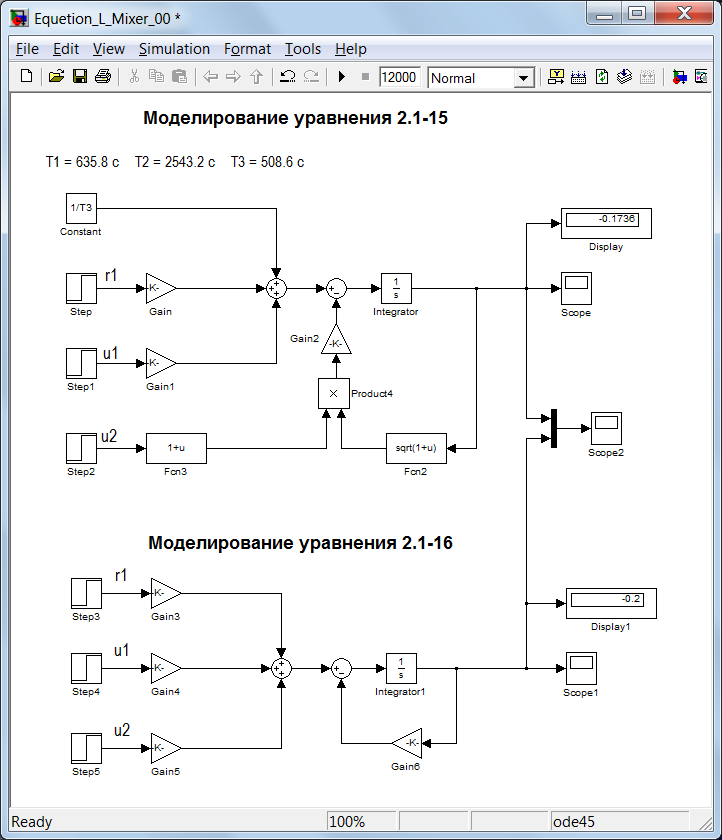
Рис. 1.3. Схемы моделирования уравнений (2.1-15) и (2.1-16)
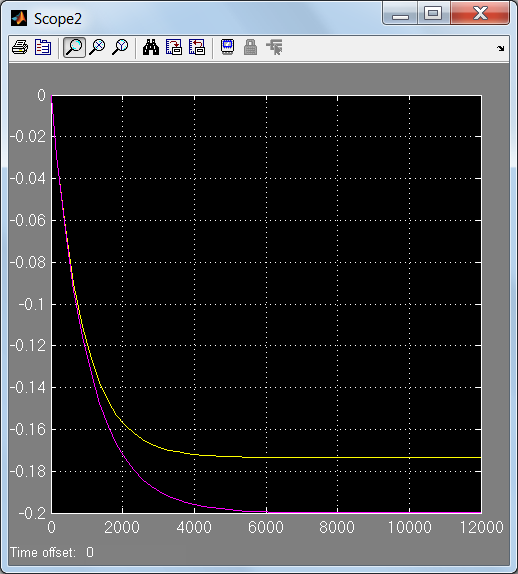
Рис. 1.4. Динамика изменения выходных величин y2 при u2=0.1
Пример 2.2
Линеаризовать нелинейные уравнения движения ДС
 (2.2-1)
(2.2-1)
вблизи окрестности стационарной точки  при
при 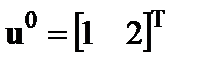 и представить полученные уравнения в матричной форме.
и представить полученные уравнения в матричной форме.
Решение
Линеаризацию системы уравнений ДС можно провести двумя способами:
1. Линеаризовать каждое уравнение системы с последующим их объединением и представлением в виде векторного дифференциального уравнения (1.11);
2. На основе уравнения (1.8) с использованием матрицы Якоби с последующим представлением векторным дифференциальным уравнением вида (1.11).
Так как функции в системе (2.2-1) аналитические, то допускают разложение в ряд Тейлора.
1. Продифференцируем каждое уравнение системы (2.2-1) по входящим в него параметрам, получаем
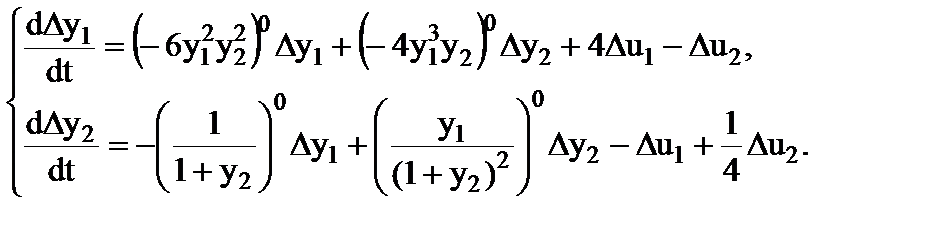
(2.2-2)
Перенесем члены с параметрами  в левую часть. Учитывая, что
в левую часть. Учитывая, что  , вынесем
, вынесем  за скобки, получим
за скобки, получим
 (2.2-3)
(2.2-3)
Введем векторы  ,
,  и представим систему уравнений (2.2-3) в форме (1.11), получим
и представим систему уравнений (2.2-3) в форме (1.11), получим
 . (2.2-4)
. (2.2-4)
2. Введем векторы  ,
,  . Представим систему уравнений (2.2-1) в виде (1.1), где
. Представим систему уравнений (2.2-1) в виде (1.1), где
 ,
,  .
.
В соответствии с уравнением (1.8) находим якобианы и получаем
 .
.
(2.2-5)
Учитывая, что  , вынесем
, вынесем  за скобки и получим линеаризованную систему в форме (1.11)
за скобки и получим линеаризованную систему в форме (1.11)
 . (2.2-6)
. (2.2-6)
Для получения линеаризованных уравнений в численной форме необходимы значения выходных и входных величин и их частных производных в стационарном состоянии ДС (2.2-1). Значения выходных величин  при
при  определяются из системы уравнений
определяются из системы уравнений
 (2.2-7)
(2.2-7)
Решение данной системы уравнений проведем в MATLAB с использованием функции solve.
Ниже приведен листинг программы с результатами решения.
>> syms y1 y2;
>> S=solve('2*y1^3*y2^2=2', 'y1/(1+y2)=0.5', y1, y2)
S =
y1: [5x1 sym]
y2: [5x1 sym]
>> S.y1
ans =
1.0
0.426*i - 0.444
0.680*i + 0.444
0.444 - 0.680*i
- 0.426*i - 0.444
>> S.y2
ans =
1.0
0.852*i - 1.888
1.361*i - 0.112
- 1.361*i - 0.112
- 0.852*i - 1.888
Учитывая физическую природу рассматриваемой системы (ХТП и ХТС) берем стационарное состояние  , определяемое действительными значениями.
, определяемое действительными значениями.
В численной форме соответственно получаем
 (2.2-8)
(2.2-8)
Пример 2.3
Линеаризовать нелинейные уравнения движения ДС
 (2.3-1)
(2.3-1)
вблизи окрестности стационарной точки  при
при 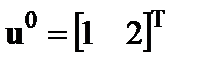 и представить полученные уравнения в матричной форме.
и представить полученные уравнения в матричной форме.
Решение
Введем векторы  ,
,  . Представим систему уравнений (2.3-1) в виде (1.1), где
. Представим систему уравнений (2.3-1) в виде (1.1), где
 ,
,  .
.
В соответствии с уравнением (1.8) находим якобианы и получаем

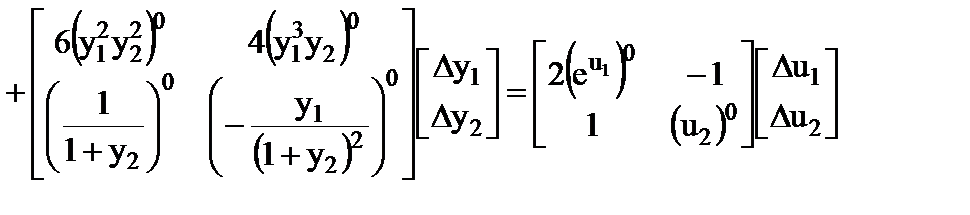 .
.
(2.3-2)
Следовательно, математическая модель линеаризованной непрерывной многосвязной системы в физических переменных «вход-выход» может быть представлена векторным дифференциальным уравнением вида (1.11)
 .
.
(2.3-3)
Для получения линеаризованных уравнений в численной форме необходимы значения выходных и входных величин и их частных производных в стационарном состоянии ДС (2.3-1). Значения выходных величин  при
при  определяются из системы уравнений
определяются из системы уравнений
 (2.3-4а)
(2.3-4а)
или
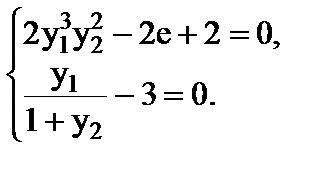 (2.3-4б)
(2.3-4б)
Решение данной системы уравнений проведем в MATLAB с использованием функции solve.
Ниже приведен листинг программы с результатами решения.
>> syms y1 y2;
S=solve('2*y1^3*y2^2=2*2.72-2', 'y1/(1+y2)=3', y1, y2)
S =
y1: [5x1 sym]
y2: [5x1 sym]
>> S.y1
ans =
3.58
1.85 - 0.77*i
0.77*i + 1.85
- 0.81*i - 0.64
0.81*i - 0.64
>> S.y2
ans =
0.19
- 0.26*i - 0.38
0.26*i - 0.38
- 0.27*i - 1.21
0.27*i - 1.21
Учитывая, что рассматривается ХТП или ХТС, то берем стационарное состояние  , определяемое действительными значениями.
, определяемое действительными значениями.
В численной форме соответственно получаем
 . (2.3-5)
. (2.3-5)
Пример 2.4
Линеаризовать нелинейные уравнения математической модели динамического режима ферментера типа ФЕМН.
Рассмотрим процесс накопления биомассы анаэробных микроорганизмов в емкостном аппарате с перемешиванием (рис.5). Кинетика процесса лимитируется концентрацией субстрата в ферментационной среде, экономический коэффициент по субстрату  (выход биомассы на единицу массы потребленного субстрата) имеет постоянное значение, дополнительная подача воздуха в ферментер отсутствует ( P=0 ). Математическая модель ферментера при данных условиях имеет вид
(выход биомассы на единицу массы потребленного субстрата) имеет постоянное значение, дополнительная подача воздуха в ферментер отсутствует ( P=0 ). Математическая модель ферментера при данных условиях имеет вид  :
:
 , (2.4-1)
, (2.4-1)
 , (2.4-2)
, (2.4-2)
где X и S – концентрации биомассы в объеме ферментационной среды, S0 – концентрация субстрата в питательном потоке, 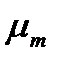 - предельное значение удельной скорости роста биомассы, Ks – константа насыщения, D – скорость разбавления,
- предельное значение удельной скорости роста биомассы, Ks – константа насыщения, D – скорость разбавления,  -экономический коэффициент по субстрату, t – время пребывания среды в аппарате.
-экономический коэффициент по субстрату, t – время пребывания среды в аппарате.
С целью сокращения числа параметров модели и обобщения результатов представим математическую модель ферментера в безразмерном виде. Для этого введем обозначения:





 (2.4-3)
(2.4-3)
Дать физический смысл обозначениям.
Выразив через них абсолютные величины и подставив их в уравнения (2.4-1) и (2.4-2), получим математическую модель ферментера непрерывного действия в безразмерном виде.
Поведение ферментера в динамике описывается системой нелинейных дифференциальных уравнений (2.4-4) и (2.4-5), записанных в безразмерном виде
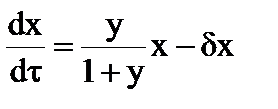 , (2.4-4)
, (2.4-4)
 . (2.4-5)
. (2.4-5)
В общем виде представленные выше зависимости можно записать как:
 и
и  .
.
Переменные x и y представляют собой обобщенные переменные состояния ферментера, характеризующие условия протекания процесса в нем, а y0 и  - обобщенные переменные управления, используемые для корректировки хода процесса (как их использовать?).
- обобщенные переменные управления, используемые для корректировки хода процесса (как их использовать?).

Рис. 5. Проточный ферментер непрерывного действия.
Исследуем протекание процесса ферментации в окрестности стационарного режима. Линеаризованную модель запишем в абсолютных отклонениях переменных от стационарного состояния.
Стационарный режим характеризуется значениями входных переменных  и y0 =y00 . Выходные переменные ферментера при заданном стационарном режиме определяются по зависимостям
и y0 =y00 . Выходные переменные ферментера при заданном стационарном режиме определяются по зависимостям
 и x0 = y00- y0. (2.4-6)
и x0 = y00- y0. (2.4-6)
Математическая модель стационарного режима ферментера имеет вид
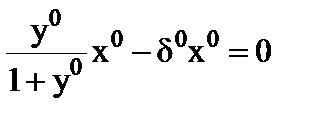 , (2.4-7)
, (2.4-7)
 . (2.4-8)
. (2.4-8)
Для линеаризации разложим уравнения (2.4-7) и (2.4-8) в ряд Тейлора и отбросим слагаемые второго и более высокого порядка малости. В результате получим

(2.4-9)

 . (2.4-10)
. (2.4-10)
Для переноса начала координат в точку стационарного режима (x0,y0) проведем вычитание уравнений (2.4-7) и (2.4-8) из уравнений (2.4-9) и (2.4-10), принимая во внимание, что 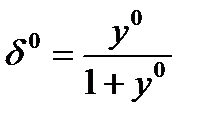
 из уравнения (2.4-7) получим:
из уравнения (2.4-7) получим:


Линеаризованная математическая модель ферментера в абсолютных отклонениях окончательно может быть представлена в виде:
 , (2.4-11)
, (2.4-11)
 , (2.4-12)
, (2.4-12)
где A= 

Полученная система линейных уравнений описывает динамику рассматриваемого ферментера в окрестности стационарного режима.
ЗАДАЧИ
Линеаризовать нелинейные уравнения движения ДС вблизи окрестности стационарной точки  при заданном значении
при заданном значении  и представить полученные уравнения в матричной форме:
и представить полученные уравнения в матричной форме:
3.1
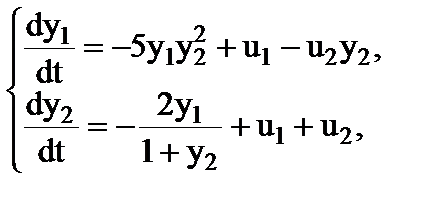 при
при  . .
|
3.2
 при
при 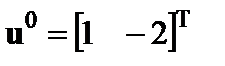 . .
| |
3.3
 при при  . .
| 3.4
 при при  . .
| |
3.5
 при
при  . .
|
3.6
 при
при  . .
| |
3.7
 при
при  . .
|
3.8
 при
при  . .
| |
3.9
 при
при 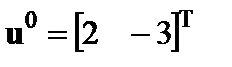 . .
|
3.10
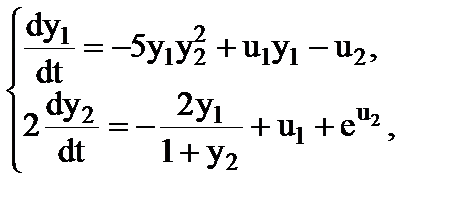 при
при 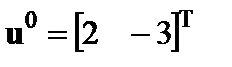 . .
| |
3.11
 при при  . .
|
3.12
 при при  . .
| |
ЛИТЕРАТУРА
| 1. | Чаки Ф. Современная теория управления. Нелинейные, оптимальные и адаптивные системы. – М.: Мир, 1975 – 424 с. |
| 2. | Янушевский Р.Т. Теория линейных оптимальных многосвязных систем управления. М.: Наука, 1973 – 464 с. |
| 3. | Инженерные основы биотехнологии. Учебное пособие для студентов Высшей инженерной школы. Под редакцией проф. Д.Г. Победимского. М.: ИПЦ МИТХТ, 1998 – 387с. |
Издание учебное
Божко Виктор Иванович
Ирина Павловна Титова
ЗАДАЧИ ПО ТЕОРИИ АВТОМАТИЧЕСКОГО
УПРАВЛЕНИЯ
Часть 1. Линеаризация уравнений движения нелинейной
динамической системы.
Учебное пособие
Подписано в печать Формат 60х84/16. Бумага писчая. Отпечатано на ризографе. Уч. издательских листов ……....
Тираж 100 экз. Заказ №
Московский государственный университет тонких химических технологий им. М.В. Ломоносова
Издательско-полиграфический центр
119571 Москва, пр. Вернадского, 86.
|
из
5.00
|
Обсуждение в статье: ПЕРВЫЙ ТЕСТОВЫЙ МЕТОД ЛЯПУНОВА |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

