Пояснения к ЛАБОРАТОРНОЙ РАБОТЕ 1

ЛАБОРАТОРНАЯ РАБОТА 1.

СРАВНЕНИЕ ДВУХ СЕРИЙ ИЗМЕРЕНИЙ.

Заданы результаты двух серий измерений (две случайные выборки).

 

I. Обработка результатов экспериментов.

 

1. Записать выборку объема n=n₁+n₂ в виде группированного статистического ряда. Для этого интервал, содержащий все элементы выборки, разбить на k непересекающихся интервалов. Вычислить частоты, частости. Найти эмпирическую функцию распределения и построить ее график.

2. Построить гистограмму и полигон частот группированной выборки.

3. Найти моду и медиану объединённой выборки по группированному статистическому ряду, сравнить их с модой и медианой негруппированного статистического ряда этой выборки.

 

II. ТОЧЕЧHЫE OЦEHKИ ПAPAMETPOB.

Найти по каждой серии оценку математического ожидания, дисперсии и среднеквадратического отклонения.

 

III. ИНТЕРВАЛЬНЫЕ ОЦЕНКИ.

Построить доверительные интервалы для полученных оценок при заданной доверительной вероятности (надежности) Р = 0.95.

 

IV. ПРОBEPKA CTATИCTИЧECKИX ГИПОТЕЗ.

Проверить:

1. Гипотезу о равенстве дисперсий ( критерий Фишера );

2. Гипотезу о равенстве математических ожиданий ( критерий Стьюдента );

3. Гипотезу о нормальном распределении объединенных данных двух выборок ( c2-критерий Пирсона).

 

При проверке гипотез с помощью критериев Фишера и Стьюдента рассчитать сводные значения оценок математического ожидания, дисперсии и среднеквадратического отклонения, а также оценку среднеквадратического отклонения по объединенной выборке объема n=n₁+n₂. Для проверки гипотезы с помощью критерия Пирсона рассчитать границы интервалов равной вероятности Р = , где L задано в условии курсовой работы (самую левую границу взять -¥, самую правую ¥).

По всем гипотезам сделать выводы.

 

Условие варианта содержит:

 

· число измерений n;

· результаты измерений первой и второй серий;

· L - число интервалов равной вероятности для проверки гипотезы Пирсона.

При выполнении работы принять следующие обозначения:

– оценка математического ожидания по 1 и 2 сериям;

– оценка дисперсий по 1 и 2 сериям;

S₁, S₂ – оценка среднеквадратического отклонения по 1 и 2 сериям;

– сводные оценки математического ожидания и стандартного отклонения;

S_об – оценка стандартного отклонения по объединенным данным;

F^* – вычисленное значение критерия Фишера;

T^* – вычисленное значение критерия Стьюдента;

^* – вычисленное значение критерия Пирсона.

В конце задания необходимо сделать выводы по гипотезам и привести окончательные числовые результаты в виде таблицы:

 

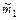
	S1	F*
	S2	T*
		*

 

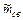
Пояснения к ЛАБОРАТОРНОЙ РАБОТЕ 1.

 

 

I. Обработка результатов эксперимента.

Одной из основных задач математической статистики является сбор и группировка статистических сведений, полученных в результате наблюдений или эксперимента. Совокупность данных называется выборкой, их количество – объемом выборки, разность между большим и меньшим элементами – размахом выборки. При достаточно большом объеме выборки неудобно представлять наблюдения перечислением. В этом случае используется понятие статистического ряда или группированного статистического ряда. В данной работе необходимо рассмотреть выборку объема n = n₁ + n₂, где n₁ – число данных по первой серии измерений, n₂ – по второй серии и записать ее в виде группированного статистического ряда. Для этого интервал, соответствующий размаху выборки и содержащий все ее элементы, разбить на k непересекающихся интервалов (kнаходится по формуле с округлением до ближайшего целого значения). Вычислить частоты z_i – количество данных по двум сериям, попавших в i - тый интервал и относительные частоты (частости) 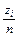. Относительная частота является точечной оценкой вероятности попадания в i -тый интервал. Если элемент совпадает с верхней границей интервала, то его нужно отнести к последующему интервалу, если он совпадает с нижней границей, то он учитывается в данном интервале. После вычислений необходимо проверить условия , где n – объем выборки. Затем вычисляются накопленные частоты - количество элементов, попавших в интервалы с 1-го по i – тый и относительные накопленные частоты , где j – указывает номер интервала, - частота элементов в j – том интервале. Относительные частоты характеризуют эмпирическую плотность распределения, а накопленные относительные частоты – эмпирическую функцию распределения. Затем все результаты сводятся в таблицу, называемую таблицей частот группированной выборки:

 

Номер интервала	Границы интервала	Середина интервала	Частота zi	Накопленная частота	Относитель-ная частота	Накопленная относитель-ная частота

 

По результатам второго и последнего столбца таблицы строят график эмпирической функции распределения, а по результатам второго и четвертого – полигон частот. Для построения гистограммы дополнительно вычисляют плотности частот , где l – длина интервала, – частота элементов в i – том интервале. Таким образом, гистограмма состоит из прямоугольников с основаниями равными l и высотой .

 

II. Точечные оценки параметров.

Точечной оценкой неизвестного параметра называют приближенное значение этого параметра, полученное по данным выборки, вычисленное с помощью определенных формул и описанное одним числом.

Пусть в результате эксперимента проведены две серии измерений и в каждой серии получены n значений: x₁, x₂, …, x_n. Для каждой серии измерений необходимо рассчитать статистическое среднее , статистическую дисперсию и эмпирический стандарт S по следующим формулам:

 

,

 

где n – число измерений в каждой серии, равное n₁ или n₂.

При вычислении статистической дисперсии 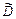деление на n–1 обусловлено выполнением требования несмещенности оценки.

Таким образом, на первом этапе выполнения работы должны быть получены 6 точечных оценок: для первой серии - = S₁; для второй серии - = S₂.

При выборке малого объема точечная оценка может серьезно отличаться от оцениваемого параметра, т.е. приводить к грубым ошибкам. Поэтому при небольшом объеме выборки следует пользоваться интервальными оценками.

 

III. Интервальные оценки параметров.

 

Интервальной называют оценку, которая определяется двумя числами – границами интервала. Интервальная оценка связана с понятием доверительного интервала. Для построения доверительного интервала необходимо знать вероятность попадания в этот интервал. Она называется надежностью, в данной работе задается Р=0.95. Число a=1–Р=0.05 называется уровнем значимости.

Необходимо построить доверительные интервалы по каждой серии измерений для математического ожидания и среднеквадратического отклонения, предполагая, что результаты измерений независимы и имеют нормальное распределение с одинаковыми параметрами m и s.

Для математического ожидания доверительный интервал имеет вид:

,

где 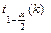- квантиль распределения Стьюдента с k = n–1 степенями свободы.
В зависимости от числа степеней свободы k и параметра = 1–0.025 = 0.975 квантиль считывается из таблиц, приведенных в Приложении. Параметры выбираются из соответствующей серии измерений.

При построении доверительного интервала для среднеквадратического отклонения используют известный результат для дисперсии. Выполнив соответствующие преобразования, получают интервал:

,

где 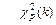- квантиль -распределения (или Пирсона), считывается из таблиц Приложения в зависимости от числа степеней свободы k = n–1 и параметра р; S, n выбираются из соответствующей серии измерений.

В работе рассчитываются границы доверительных интервалов для оценок m₁, s₁ первой серии измерений и для m₂, s₂ второй серии.

 

Замечание: вычисляемое математическое ожидание может рассматриваться как приближение истинного значения измеряемой величины, а стандартное отклонение характеризует абсолютную погрешность измерений. Доверительные интервалы показывают степень близости полученных оценок к истинным значениям соответствующих величин.

 

 

IV. Проверка гипотез.

 

Во многих случаях результаты наблюдений используются для проверки предположений относительно различных свойств и параметров распределения генеральной совокупности. Такие предположения называются статистическими гипотезами. Правило, по которому принимают решение принять или отклонить поставленную гипотезу, называется критерием. В работе проверяются 3 гипотезы: о равенстве дисперсий (критерий Фишера), о равенстве математических ожиданий (критерий Стьюдента) и о нормальности распределения объединенных данных ( 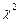- критерий или Пирсона).

 

1.Проверить гипотезу о равенстве дисперсий (критерий Фишера).

Проверяемая гипотеза Н₀ –дисперсии обеих серий равны. Пусть 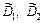- оценки дисперсий по первой и второй сериям измерений с числом степеней свободы k₁ = n₁-1 и k₂ = n₂-1 соответственно. Разделив большую эмпирическую дисперсию на меньшую, составим статистику и сравним ее с квантилью распределения Фишера , где p = = 0.975, k₁=n₁-1, k₂=n₂-1 - число степеней свободы. - выбирается из соответствующих таблиц, приведенных в Приложении. Если полученное значение F* больше табличного ( F* > F ), то следует признать расхождение значительным (т. е. отвергнуть гипотезу о равенстве дисперсий в двух сериях измерений), в противном случае ( F* < F ) гипотезу о равенстве дисперсий принимают, как не противоречащую результатам измерений ( с уровнем значимости 5% ). После проверки гипотезы вычислить сводную оценку дисперсии

.

Замечание: сравнивая дисперсии, определяем, одинакова ли погрешность измерений в двух сериях.

 

2.Проверить гипотезу о равенстве математических ожиданий (критерий Стьюдента).

Проверяемая гипотеза Н₀ – математические ожидания обеих серий равны. Пусть 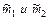- оценки математических ожиданий по двум сериям. Причём в зависимости от выводов, сделанных по результатам проверки гипотезы Фишера имеем два варианта проверки этой гипотезы.

а). Гипотеза о равенстве дисперсий принимается (не отклоняется).

Составим статистику – отношение Стьюдента , где . Полученное значение T^* необходимо сравнить с вычисленной по таблице квантилью распределения Стьюдента T_табл(p, k), где р = , k = n₁ + n₂ - 2.

Если | T | > T_табл(p, k), то гипотезу о равенстве математических ожиданий отвергают, как противоречащую результатам эксперимента, в противном случае – гипотезу принимают.

в). Гипотеза о равенстве дисперсий отклоняется.

В этом случае статистика – отношение Стьюдента имеет вид .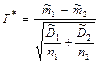

Полученное значение T^* необходимо сравнить с вычисленной по таблице квантилью распределения Стьюдента T_табл(p, k), где р = , k = .

Далее проверка проводится так же, как в случае а). После проверки гипотезы необходимо вычислить сводную оценку математического ожидания по формуле:

Замечание: если гипотеза о равенстве математических ожиданий принимается, то это можно трактовать как принадлежность обеих выборок одной и той же нормальной совокупности.

 

3.Проверить гипотезу о нормальном распределении объединенных данных из двух серий (критерий Пирсона или ).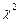

Проверяемая гипотеза Н₀ – генеральная совокупность распределена нормально.

По объединенной выборке наблюдений необходимо найти оценки параметров предполагаемого нормального распределения: , где 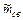найдена при проверке критерия Стьюдента, вычисляется по объединенной выборке из двух серий. Затем область всех значений случайной величины Х разбивается на L интервалов равной вероятности, т.е. такие, вероятность попадания измеряемой величины в каждый из которых одинакова и равна p = 1/L. При этом левая граница выбирается -¥, а правая +¥ (см. пояснения). Подсчитав n_i – число попаданий измеряемой величины в i - й интервал (по двум сериям), вычислим статистику

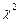= , где n=n₁+ n₂ , p = .

Полученное значение необходимо сравнить с табличной квантилью распределения Пирсона при уровне значимости a = 5% с k = L-3 степенями свободы. Если 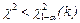, то можно считать, что при заданном уровне значимости a = 5% гипотеза о нормальном распределении генеральной совокупности не противоречит результатам эксперимента. В противном случае гипотезу отвергают. На практике необходимо повторить измерения величины Х.