МАТРИЦА ПЕРЕХОДА. КООРДИНАТЫ ВЕКТОРОВ

Лабораторная работа 8

ЛИНЕЙНОЕ ПРОСТРАНСТВО. ПОДПРОСТРАНСТВО.

БАЗИС И РАЗМЕРНОСТЬ

 

Вопросы для самоконтроля:

1.Какое множество называется линейным пространством?

2.Какие операции определены в линейном пространстве?

3.Что такое подпространство?

4.Выполнение каких условий достаточно проверить для того, чтобы убедиться, что некоторое подмножество линейного пространства является его подпространством?

5.Что называется линейной оболочкой конечной системы векторов?

6.Что такое базис линейного пространства?

7.Что такое размерность линейного пространства?

8.Какое линейное пространство называется конечномерным?

9.Как найти базис линейной оболочки?

 

ВАРИАНТ 1

1.Является ли линейным пространством множество всех радиус-векторов точек первой четверти прямоугольной декартовой системы координат?

2.Доказать, что множество A={(α₁,0,α₂,0)|α₁,α₂ÎR} составляет подпространство пространства A₄. Найти его базис и размерность.

3.Найти базис и размерность линейной оболочки векторов
a₁=(5,2,-3,1), a₂=(4,1,-2,3), a₃=(1,1,-1,-2), a₄=(3,4,-1,2).

 

ВАРИАНТ 2

1.Является ли линейным пространством множество всех радиус-векторов точек, некоторой прямой. Найти его базис и размерность.

2.Доказать, что множество A={(α₁,α,α₂,α)|α,α₁,α₂ÎR} составляет подпространство пространства A₄. Найти его базис и размерность.

3.Найти базис и размерность линейной оболочки векторов a₁, a₂, a₃, a₄, a₅, где a₁=1+2x+3x²–4x³, a₂=2+3x–4x²+x³, a₃=2–5x+8x²–3x³, a₄=5+26x–9x²–12x³, a₅=3–4x+x²+2x³.

 

ВАРИАНТ 3

1.Является ли линейным пространством множество всех векторов плоскости за исключением векторов, параллельных заданной прямой.

2.Доказать, что множество A={f(x)=a₀+a₁x+…+a_nxⁿ, a₀,…,a_nÎR, f(0)=0} составляет подпространство пространства P_n. Найти его базис и размерность.

3.Найти базис и размерность линейной оболочки векторов

, , , , .

 

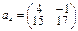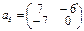ВАРИАНТ 4

1.Составляет ли линейное пространство множество многочленов A={f(x)=a₀+a₁x+…+a_nxⁿ|a₀,…,a_nÎR}? Найти его размерность и базис.

2.Доказать, что множество A={(α,α₁,α₂,α₃,α) | α,α₁,α₂,α₃ÎR} составляет подпространство пространства A₅. Найти его базис и размерность.

3.Найти базис и размерность линейной оболочки векторов a₁=e₁+2e₂+3e₃+4e₄, a₂=2e₁+3e₂+4e₃+5e₄, a₃=3e₁+4e₂+5e₃+6e₄, a₄=4e₁+5e₂+6e₃+7e₄; e₁, e₂, e₃, e₄ – базис линейного пространства L.

 

 

ВАРИАНТ 5

1.Образует ли линейное пространство множество многочленов A={a₀xⁿ+a₁xⁿ⁺¹+…+a_kx^n+k | nÎN, a₀,…,a_kÎR, k=0,1,2,…}? Указать его базис и размерность.

2.Доказать, что множество всех решений однородной системы линейных уравнений с n неизвестными образует подпространство пространства A_n. Найти его базис и размерность.

3.Найти базис и размерность линейной оболочки векторов
a₁=2–x+3x²–2x³+4x⁴, a₂=7x⁴+x³+5x²–2x+4, a₃=2+x²–x+8x³+2x⁴.

 

ВАРИАНТ 6

1.Во множестве S={(α₁,α₂,…)|α_iÎN, i=1,2,3,…} введены операции сложения x+y=(α₁,…)+(β₁,…)=(α₁+β₁,…) и умножения на действительное число k: kx=k(α₁,α₂,…)=(kα₁,kα₂,…). Является ли S линейным пространством, если α_iÎR, i=1,2,3,…? Указать его базис и размерность.

2.Образует ли подпространство пространства V₂ множество радиус-векторов точек некоторой прямой? Указать его базис и размерность.

3.Найти базис и размерность линейной оболочки векторов

, , , .

 

 

ВАРИАНТ 7

1.Образуют ли линейное пространство множество матриц M? Указать его базис и размерность.

.

2.Составляет ли подпространство пространства P₅ множество A={a₀+a₂x²+a₄x⁴ | a₀,a₂,a₄ÎR}? Указать его базис и размерность.

3.Найти базис и размерность линейной оболочки векторов a₁=x⁵+x⁴+x+1, a₂= –1, a₃=2x²+5x, a₄=2x³–2.

 

ВАРИАНТ 8

1.Является ли множество матриц M линейным пространством? Найти его базис и размерность.

.

2.Доказать, что множество 6-мерных векторов A={(α,β,α,β,α,β)| α,βÎR} составляет подпространство пространства A₆. Найти его базис и размерность.

3.Найти базис и размерность линейной оболочки векторов
a₁, a₂, a₃, a₄, где a₁=e₁+e₂+e₃+e₄, a₂= – e₅ – e₄ – e₃+e₂+e₁, a₃=2e₁+2e₂ – e₅, a₄=2e₅+5e₄+5e₃+e₂+e₁, a₅= – e₃ – e₂+e₁;

e₁, …, e₅ – базис линейного пространства.

 

ВАРИАНТ 9

1.Составляет ли линейное пространство множество двумерных векторов A₂={(α,β)|α,βÎR} с операциями сложения x+y=(α,β)+(γ,δ)=(α+γ,β+δ) и умножения на действительное число k kx=k(α,β)=(kα,kβ)? Найти его базис и размерность.

2.Доказать, что множество матриц A составляет подпространство пространства M₃. Найти его базис и размерность.

.

3.Найти базис и размерность линейной оболочки векторов
a₁=3–x+3x²+2x³+5x⁴, a₂=5–3x+2x²+3x³+4x⁴,

a₃=1–3x–5x²–7x⁴, a₄=x⁴+4x³+x²–5x+7.

ВАРИАНТ 10

1.Доказать, что множество M₂ образует линейное пространство. Найти его базис и размерность.

.

2.Образует ли подпространство пространства A_n множество A={(x₁,…,x_n) | x_iÎR, x₁+…+x_n=0}? Найти его базис и размерность.

3.Найти базис и размерность линейной оболочки векторов
a₁=(4,3,-5,2,3), a₂=(8,6,-7,4,2),a₃=(4,3,-8,2,7),a₄=(4,3,1,2,-5).

 

ВАРИАНТ 11

1.Составляет ли линейное пространство множество векторов:

a) A={(x₁,…,x_n) | x_i – четные числа, i=1,2,…,n};

б) B={(x₁,…,x_n) | x_i – нечетные числа, i=1,2,…,n}?

2.Составляет ли множество многочленов A={f(x)=a₀+a₁x+…+a_nxⁿ, a_iÎR, i=1,2,…,n, a₀+…a_n=0} подпространство пространства P_n? Найти его базис и размерность.

3.Найти базис и размерность линейной оболочки векторов
a₁=e₁–e₂+e₃, a₂=e₁+e₂+e₄, a₃=2e₁+e₃+e₄; e₁, e₂, e₃, e₄ – базис линейного пространства L.

 

ВАРИАНТ 12

1.Составляет ли линейное пространство множество матриц A? Найти его базис и размерность.

.

2.Доказать, что множество A составляет подпространство пространства A_n. Найти его базис и размерность.

.

3.Найти базис и размерность линейной оболочки векторов a₁=x+2x²+3x³–2x⁴+x⁵, a₂=3x⁵–4x⁴+5x³+6x²+3x,

a₃=x²+x–4x⁴+7x³+x⁵, a₄=2x+4x²–2x³–3x⁴+3x⁵.

 

ВАРИАНТ 13

1.Составляет ли множество многочленов A={f(x)=a₁x+a₃x³+a₅x⁵| a₁,a₃,a₅ÎR} линейное пространство? Найти его базис и размерность.

2.Составляет ли множество матриц A подпространство пространства M₂? Найти его базис и размерность.

.

3.Найти базис и размерность линейной оболочки векторов
a₁=1–x+x²–x³+x⁴, a₂=7x⁴–x³+x²+x+3, a₃=1+x+3x⁴, a₄=2x⁴+x³–x²+2x.

 

 

Лабораторная работа 9

МАТРИЦА ПЕРЕХОДА. КООРДИНАТЫ ВЕКТОРОВ

 

Вопросы для самоконтроля:

1.Что называется столбцом координат (координатами) вектора в некотором базисе?

2.Дайте определение матрицы перехода от одного базиса к другому в линейном пространстве?

3.При составлении матрицы перехода координаты векторов нового базиса в старом надо располагать в строки или столбцы этой матрицы?

4.Если T – матрица перехода от первого базиса ко второму, то какой будет матрица перехода от второго базиса к первому?

5.Как связаны координаты одного и того же вектора в разных базисах?

 

ВАРИАНТ 1

1.Матрица M является матрицей перехода от базиса e₁, e₂, e₃ к базису a₁, a₂, a₃. Найти координаты векторов e₁, e₂, e₃ и вектора x = 2e₁–e₃ в базисе a₁, a₂, a₃.

.

2.В пространстве многочленов, степени которых не превосходят 3, найти матрицу перехода от базиса 1, x, x², x³ к базису 3, 3x+5, (x+3)², (x–4)³.

3.Найти связь координат одного и того же вектора в двух базисах e₁=1–x, e₂=2 и a₁=3+2x, a₂=4+3x.

 

ВАРИАНТ 2

1.Убедиться, что a₁=(1,2,-3), a₂=(4,2,-8), a₃=(1,4,-1) образуют базис линейного пространства A₃. Найти координаты вектора b=(7,-1,-2) в базисе a₁, a₂, a₃.

2.В пространстве многочленов, степени которых не превосходят 2, найти матрицу перехода от базиса x²+3x–2, 3x–1,5 к базису 1, x, x²+3.

3. Матрица Т является матрицей перехода от базиса e₁, e₂ к базису f₁, f₂. Найти координаты векторов e₁, e₂, c=2e₁+3e₂ в базисе f₁, f₂.

.

 

ВАРИАНТ 3

1.Даны два базиса линейного пространства A₃:

1) e₁=(1,1,1), e₂=(2,1,1), e₃=(1,0,1) и

2) f₁=(0,1,1), f₂=(1,0,1), f₃=(1,0,2). Найти матрицу перехода от базиса (1) к базису (2), и наоборот.

2.Найти координаты многочлена f(x)=x²+8x–24 в базисе 3x²+2x–1, 3x+4, x²+3x–2.

3.Убедиться, что многочлены 2, x–3, (2–x)², (x+4)³ составляют базис пространства P₃. Найти матрицу перехода от базиса 1, x, x², x³ к базису 2, x–3, (2–x)², (x+4)³.

 

ВАРИАНТ 4

1.Даны два базиса линейного пространства: e₁=(1,2), e₂=(2,3) и e₁’=(4,5), e₂’=(1,1). Найти связь координат одного и того же вектора в этих базисах.

2.Убедиться, что многочлены f₁=x²–3x+1, f₂=4x+3x², f₃=x² составляют базис линейного пространства многочленов, степени которых не превосходят 2. Найти координаты многочлена g(x)=5x²–5x+3 в этом базисе.

3.Убедиться, что многочлены 2, x–3, (x–2)² составляют базис пространства P₂. Найти матрицу перехода от базиса 2, x–3, (x–2)² к базису 1, x, x².

 

ВАРИАНТ 5

1.Найти связь координат одного и того же вектора в двух базисах: a₁=(1,2), a₂=(2,1) и b₁=(2,3), b₂=(4,1).

2.Найти матрицу перехода от базиса 1, x, x², x³ к базису 4, x²+1, x³+3x–1, x³+2x–1.

3.Даны два базиса a₁, a₂ и b₁, b₂, причем a₁=3b₁+5b₂, a₂=2b₁+3b₂. Найти координаты вектора c=3b₁+2b₂ в базисе a₁, a₂.

 

ВАРИАНТ 6

1.Найти матрицу перехода от базиса a₁=(1,2,3), a₂=(4,0,-1), a₃=(2,2,0) к базису e₁=(1,0,0), e₂=(0,1,0), e₃=(0,0,1).

2.Найти координаты многочлена f(x)=5x²–3x+6 в базисе 4, 4x+3, x²–3x+1.

3.Найти связь координат вектора в двух базисах: a₁=3+2x, a₂=4+3x и e₁=1–x, e₂=2.

 

ВАРИАНТ 7

1.Убедиться, что векторы a₁=(1,2,3), a₂=(2,3,-1), a₃=(2,0,1) образуют базис линейного пространства A₃. Найти координаты вектора x=(0,-7,-3) в этом базисе.

2.В пространстве многочленов, степени которых не превосходят 2, найти матрицу перехода от базиса x, x²+2x, x²–3x+1 к базису 4, 4x–2, x²+x–3.

3.Матрица М является матрицей перехода от базиса a₁=(1,2), a₂=(3,2) к базису b₁, b₂. Найти координаты вектора c=2a₁+a₂ в базисе b₁, b₂.

.

 

ВАРИАНТ 8

1.Найти матрицу перехода от базиса e₁’=e₁, e₂’=e₁+e₂, e₃’=e₁+e₂+e₃ к базису e₁, e₂, e₃.

2.Убедиться, что многочлены f₁=x²+3x+1, f₂=–1+4x², f₃=x²–2x составляют базис пространства P₂ многочленов, степени которых не превосходят 2. Найти координаты многочлена g(x)=3x²–8x–3 в этом базисе.

3.Матрица М является матрицей перехода от базиса x, 1, x² к базису f₁, f₂, f₃. Найти матрицу перехода от базиса f₁, f₂, f₃ к базису x, 1, x².

.

 

ВАРИАНТ 9

1.Матрица М является матрицей перехода от базиса e₁, e₂, e₃ к базису a₁, a₂, a₃. Найти координаты векторов e₁, e₂, e₃ и x=e₁+2e₂–e₃ в базисе a₁, a₂, a₃.

.

2.Для пространства P₂ многочленов, степени которых не превосходят 2, найти матрицу перехода от базиса 4x²–1, 4x+1, 3 к базису x²+2x+3, 2x, x–4.

3.Даны два базиса a₁=(1,-2), a₂=(3,-5) и b₁=(1,1), b₂=(2,3) пространства A₂ двумерных векторов. Найти матрицу перехода от базиса a₁, a₂ к базису b₁, b₂.

 

ВАРИАНТ 10

1.Найти матрицу перехода от базиса a₁=(1,2,3), a₂=(2,3,-1), a₃=(0,1,1) к базису b₁=(2,3,1), b₂=(1,1,1), b₃=(-1,2,1).

2.В пространстве P₂ многочленов, степени которых не превосходят 2, найти координаты многочлена f(x)=3x²+6 в базисе x²+x–1, x²+2x–3, x–3.

3.Матрица М является матрицей перехода от базиса 1, x, x² к базису f₁, f₂, f₃ в пространстве P₂ многочленов, степени которых не превосходят 2. Найти координаты многочлена g(x)=3x²–4x+1 в базисе f₁, f₂, f₃.

.

 

ВАРИАНТ 11

1.В пространстве P₂ многочленов, степени которых не превосходят 2, даны два базиса: 1) x, x²+4x, 3x–1 и

2) x²–3x+1, x²+1, 3x+1. Найти матрицу перехода от

базиса (1) к базису (2).

2.Убедиться, что векторы a₁=(1,2), a₂=(3,5) образуют базис пространства A₂. Найти координаты вектора x=(3,4) в базисе a₁, a₂.

3.Матрица М является матрицей перехода от базиса e₁, e₂, e₃ к базису a₁, a₂, a₃. Найти координаты вектора b=3a₁–a₂+a₃ в базисе e₁, e₂, e₃.

.

ВАРИАНТ 12

1.Матрица М является матрицей перехода от базиса e₁, e₂, e₃ к базису a₁, a₂, a₃. Найти координаты векторов e₁, e₂, e₃ и вектора x=2e₁–e₂ в базисе a₁, a₂, a₃.

.

2.Даны два базиса линейного пространства A₂ двумерных векторов: 1) a₁=(3,4), a₂=(1,1) и 2) b₁=(2,5), b₂=(1,3). Найти матрицу перехода от базиса (2) к базису (1).

3.В пространстве многочленов P₃ найти матрицу перехода от базиса 1, x, x², x³ к базису 5, 2x–3, (x–3)², (x+2)³.

 

ВАРИАНТ 13

1.Убедиться, что векторы a₁=(1,2,-3), a₂=(4,2,-8), a₃=(1,4,-1) образуют базис линейного пространства A₃. Найти координаты вектора (-1,0,5) в базисе a₁, a₂, a₃.

2.В пространстве многочленов, степени которых не превосходят 2, найти матрицу перехода от базиса x²+3x–2, 2x–3, 3 к базису 1, 3x–2, x²–4x.

3.Даны два базиса линейного пространства A₂ двумерных векторов a₁=(1,2), a₂=(3,5) и b₁=(2,1), b₂=(3,4). Найти матрицу перехода от базиса a₁, a₂ к базису b₁, b₂.