 |
Главная |
Системы линейных уравнений
|
из
5.00
|
1°. Крамеровские системы линейных уравнений.Рассмотрим систему из п линейных уравнений с п неизвестными  :
:
 (3.1)
(3.1)
Система (3.1) называется квадратной. Определитель, составленный из коэффициентов при неизвестных системы (3.1), называется главным определителем этой системы и обозначается Δ. Таким образом,
 .
.
Наряду с главным определителем системы Δ рассмотрим так называемые вспомогательные определители  , i = 1, 2,…, n, которые получаются из главного путем замены его i-го столбца на столбец свободных членов:
, i = 1, 2,…, n, которые получаются из главного путем замены его i-го столбца на столбец свободных членов:

Теорема 3.1 (теорема Крамера). Если главный определитель Δ системы (3.1) отличен от нуля, то эта система имеет единственное решение, определяемое равенствами

 (3.2)
(3.2)
Равенства (3.2) называются формулами Крамера, а система (3.1) при  называется крамеровской системой.
называется крамеровской системой.
Пример 3.1. Используя формулы Крамера, решить систему линейных уравнений

►Для отыскания решения системы по формулам (3.2) вычислим главный определитель системы Δ и вспомогательные определители  , получающиеся из Δ путем замены его первого, второго и третьего столбцов соответственно на столбец свободных членов:
, получающиеся из Δ путем замены его первого, второго и третьего столбцов соответственно на столбец свободных членов:





Теперь находим решение системы по формулам (3.2):


 .◄
.◄
Замечание 3.1. Решение крамеровской системы можно выразить в мат-ричной форме:
 (3.3)
(3.3)
где  матрица, обратная к матрице А, составленной из коэффициентов при неизвестных, Х – столбец из неизвестных, а В – столбец свободных членов.
матрица, обратная к матрице А, составленной из коэффициентов при неизвестных, Х – столбец из неизвестных, а В – столбец свободных членов.
Пример 3.2.Используя матричную форму записи, решить систему уравнений из примера 1.
►Пусть  ,
,  ,
,  .
.
Данной системе соответствует уравнение  где матрицы А и В имеют указанный смысл. Матрица А имеет обратную (найдите её самостоятельно),
где матрицы А и В имеют указанный смысл. Матрица А имеет обратную (найдите её самостоятельно),
 . С помощью равенства (3.3) найдём решение системы:
. С помощью равенства (3.3) найдём решение системы:


Таким образом, система имеет единственное решение:  .◄
.◄
2°. Решение произвольных систем линейных уравнений. Метод Гаусса. Рассмотрим системы, в которых число линейных уравнений и число неизвестных произвольны. Такие системы будем называть произвольными системами линейных уравнений. Пусть дана система из т линейных уравнений с п неизвестными  :
:
 (3.4)
(3.4)
Элементарными преобразованиями над системой линейных уравнений вида (3.4) называются:
1.перестановка местами двух любых ее уравнений;
2.умножение всех членов любого уравнения системы на любое отличное от нуля число;
3.почленное сложение любых двух ее уравнений.
Теорема 3.2.Конечное число последовательно выполненных элементарных преобразований приводят систему (3.4) к равносильной ей системе.
Матрица А, составленная из коэффициентов при неизвестных системы (3.4), называется матрицей этой системы, а матрица А* , полученная из А путём добавления  -го столбца из свободных членов, – её расширенной матрицей. Расширенная матрица системы содержит всю информацию о системе. Имеем:
-го столбца из свободных членов, – её расширенной матрицей. Расширенная матрица системы содержит всю информацию о системе. Имеем:
 ,
,  .
.
На практике элементарным преобразованиям подвергают не саму систему (3.4), а её расширенную матрицу А*. Преобразованиям над системой (3.4) будут соответствовать элементарные преобразования над строками матрицы А*:
1.перестановка местами двух любых её строк;
2.умножение всех элементов любой её строки на любое отличное от нуля
число;
3.сложение соответствующих элементов двух любых её строк.
Целью элементарных преобразований является приведение расширенной матрицы А* системы (3.4) к так называемой ступенчатой форме.
Определение 3.2. Матрица называется ступенчатой, если для нее выполняются следующие условия:
1. если какая-либо строка данной матрицы состоит из нулей, то и все последующие строки также состоят из нулей;
2. если  – первый ненулевой элемент i –той строки, а
– первый ненулевой элемент i –той строки, а  – первый ненулевой элемент (i+1)–ой строки, то
– первый ненулевой элемент (i+1)–ой строки, то 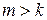 .
.
Так, например, матрица  является ступенчатой.
является ступенчатой.
Матрица из одной строки считается ступенчатой по определению.
Теорема 3.3.Любую матрицу А конечным числом элементарных преобразований можно преобразовать в ступенчатую матрицу.
На приведении расширенной матрицы А* системы (3.4) к ступенчатой матрице А1* основан метод Гаусса или метод последовательного исключения неизвестных. Система линейных уравнений с расширенной ступенчатой матрицей А1* называется ступенчатой, по теореме 3.2 она будет равносильна системе (3.4). Приведение системы (3.4) к ступенчатой форме называется прямым ходом метода Гаусса. Решение полученной ступенчатой системы называется обратным ходом метода Гаусса. Он может быть выполнен как в форме последовательного определения неизвестных, начиная с последнего уравнения ступенчатой системы, так и в форме преобразования матрицы А1* к ступенчатой матрице В* специального вида.
При решении произвольной системы линейных уравнений (т.е. системы (3.4)) реализуется один из следующих случаев.
1. Система (3.4) не имеет решений (т.е. является несовместной), если не совпадает число ненулевых строк в матрицах  и
и  , полученных в результате приведения матрицы системы А и ее расширенной матрицы A* к ступенчатой форме.
, полученных в результате приведения матрицы системы А и ее расширенной матрицы A* к ступенчатой форме.
2. Система (3.4) имеет единственной решение (т.е. является совместной и определённой), если число ненулевых строк в матрицах  и
и  одинаково и равно числу неизвестных. В этом случае система (3.4) крамеровская или равносильна такой системе.
одинаково и равно числу неизвестных. В этом случае система (3.4) крамеровская или равносильна такой системе.
3. Система (3.4) имеет бесчисленное множество решений (т.е. является совместной и неопредёленной), если число r ненулевых строк в матрицах  и
и  одинаково и меньше n – числа неизвестных. В этом случае r неизвестных, коэффициенты при которых образуют отличный от нуля определитель, принимают за базисные, а остальные n – r неизвестных – за свободные. Члены уравнений системы со свободными неизвестными переносят в правые части этих уравнений и разрешают полученную систему относительно базисных неизвестных.
одинаково и меньше n – числа неизвестных. В этом случае r неизвестных, коэффициенты при которых образуют отличный от нуля определитель, принимают за базисные, а остальные n – r неизвестных – за свободные. Члены уравнений системы со свободными неизвестными переносят в правые части этих уравнений и разрешают полученную систему относительно базисных неизвестных.
Замечание 3.1.Множество решений системы (3.4) может быть либо пустым, либо состоять из одного элемента, либо быть бесконечным. Оно не может состоять из одного, двух, трех и т. д. элементов.
Пример 3.3. Решить методом Гаусса систему уравнений 
►Прямой ход метода Гаусса. Приведем к ступенчатому виду расши-ренную матрицу системы 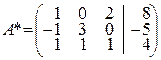 , выполнив следующие эле-ментарные преобразования над матрицей А*:
, выполнив следующие эле-ментарные преобразования над матрицей А*:
1. к элементам второй строки прибавим элементы первой строки и из элементов третьей строки вычтем элементы первой строки, в результате А* преобразуется к виду:  ;
;
2. переставим вторую и третью строку:  ;
;
3. из последней строки полученной матрицы вычтем вторую строку, умноженную на 3, получим:  .
.
Обратный ход метода Гаусса. 1-ый способ. Матрице  сопоставим систему, для которой она будет расширенной матрицей:
сопоставим систему, для которой она будет расширенной матрицей:

Имеем:

2-ый способ. Умножим последнюю строку матрицы  на 1/5, сложим со второй строкой, а к первой строке прибавим последнюю, умноженную на (–2), с целью получить нули в третьем столбце, получим
на 1/5, сложим со второй строкой, а к первой строке прибавим последнюю, умноженную на (–2), с целью получить нули в третьем столбце, получим

Напишем систему с расширенной матрицей В*: 
Ответ: система совместная и определенная, она имеет единственное решение  ◄
◄
Пример 3.4. Решить систему уравнений 
►Рассмотрим расширенную матрицу этой системы  .
.
Первые три столбца этой матрицы образуют матрицу А – матрицу коэффициентов системы. Подвергнем А* следующим элементарным преобразованиям. Переставим первую и вторую строки, затем последовательно умножим первую строку на (–2) и на (–3) и сложим со второй и третьей строками, после чего из третьей строки вычтем вторую:

Матрица А при этом преобразуется в матрицу  , составленную из первых трех столбцов матрицы
, составленную из первых трех столбцов матрицы  . Число ненулевых строк в матрицах
. Число ненулевых строк в матрицах  и
и  различно и равно 2 и 3 соответственно. Матрице
различно и равно 2 и 3 соответственно. Матрице  соответствует система
соответствует система


которая является несовместной, так как ее последнее уравнение не имеет решений. Поэтому несовместна и равносильная ей исходная система. ◄
Пример 3.5.Решить систему уравнений 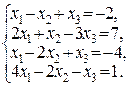
►Выпишем расширенную матрицу этой системы  и подвергнем ее элементарным преобразованиям. Умножим первую строку на числа 2, 1, 3 и вычтем ее последовательно из второй, третьей и четвертой строк, после чего поменяем местами вторую и третью строки, получим
и подвергнем ее элементарным преобразованиям. Умножим первую строку на числа 2, 1, 3 и вычтем ее последовательно из второй, третьей и четвертой строк, после чего поменяем местами вторую и третью строки, получим

 .
.
Умножим теперь вторую строку на числа 3, 2 и сложим ее последовательно с третьей и четвертой строками, после этого умножим вторую строку на  ,
,
третью строку вычтем из четвёртой, а затем третью строку умножим на  . В результате этих преобразований имеем
. В результате этих преобразований имеем
 .
.
Заметим, что число ненулевых строк в матрице  равно числу неизвестных. Матрице
равно числу неизвестных. Матрице  соответствует крамеровская система:
соответствует крамеровская система:  (её главный определитель
(её главный определитель  ). Она имеет единственное решение
). Она имеет единственное решение  . ◄
. ◄
Пример 3.6.Найти все решения системы 
►Выпишем расширенную матрицу системы
 .
.
Подвергнем матрицу  элементарным преобразованиям. Умножим первую строку на числа (–2) и (–3) и сложим последовательно со второй и третьей строкой, получим
элементарным преобразованиям. Умножим первую строку на числа (–2) и (–3) и сложим последовательно со второй и третьей строкой, получим
 .
.
Вычтем теперь вторую строку из третьей и четвертой:
 .
.
Матрице  соответствует следующая система:
соответствует следующая система: 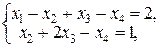 равносильная данной. Неизвестные
равносильная данной. Неизвестные  примем за базисные, а неизвестные
примем за базисные, а неизвестные  за свободные. Перенесём члены со свободными неизвестными в правые части уравнений последней системы:
за свободные. Перенесём члены со свободными неизвестными в правые части уравнений последней системы:  Отсюда имеем
Отсюда имеем

Приняв обозначения 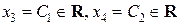 , получаем совокупность всех решений данной системы в виде:
, получаем совокупность всех решений данной системы в виде:  ◄
◄
3°. Однородные системы линейных уравнений.Рассмотрим следующую систему линейных уравнений:
 (3.5)
(3.5)
где т и п – произвольные натуральные числа. Она называется однородной системой линейных уравнений.
Система (3.5) всегда совместна, так как при любых значениях коэффициентов  она имеет так называемое нулевое, или тривиальное, решение
она имеет так называемое нулевое, или тривиальное, решение  . Решение системы (3.5), не совпадающее с тривиальным, называется ненулевым. Система (3.5) – частный случай системы (3.4), она получается из этой системы при
. Решение системы (3.5), не совпадающее с тривиальным, называется ненулевым. Система (3.5) – частный случай системы (3.4), она получается из этой системы при  .
.
Пусть А и А* – матрица и расширенная матрица системы (3.5):
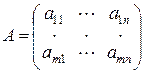 ,
, 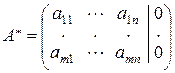 .
.
Расширенная матрица А* системы (3.5) конечным числом элементарных преобразований приводится к ступенчатому виду  , при этом первые п столбцов матрицы
, при этом первые п столбцов матрицы  образуют матрицу
образуют матрицу  , получающуюся из матрицы А при выполнении указанных преобразований. Поскольку число ненулевых строк в матрицах
, получающуюся из матрицы А при выполнении указанных преобразований. Поскольку число ненулевых строк в матрицах  и
и  всегда совпадает, то при решении однородной системы реализуется только второй или третий случай из перечисленных в пункте 2.
всегда совпадает, то при решении однородной системы реализуется только второй или третий случай из перечисленных в пункте 2.
Пример 3.7. Дана система:  Найти значения параметра β, при которых: а) нулевое решение этой системы единственно; б) данная система имеет ненулевые решения.
Найти значения параметра β, при которых: а) нулевое решение этой системы единственно; б) данная система имеет ненулевые решения.
►Данная система квадратная. Вычислим её главный определитель Δ:

а) Нулевое решение  единственно, если
единственно, если  . Это условие выполняется в случае
. Это условие выполняется в случае 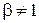 .
.
б) Система имеет ненулевые решения при  , поэтому для параметра β получаем условие
, поэтому для параметра β получаем условие  . В этом случае данная система имеет вид:
. В этом случае данная система имеет вид:
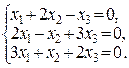
Выпишем её расширенную матрицу:
 .
.
Первые три столбца А* образуют матрицу А – матрицу коэффициентов системы. Подвергнем А* следующим элементарным преобразованиям. Последовательно умножим первую строку на (–2) и на (–3) и сложим со второй и третьей строками, затем из третьей строки вычтем вторую, после чего элементы второй строки разделим на 5:

Матрице  соответствует следующая система:
соответствует следующая система:  равносильная данной. Неизвестные
равносильная данной. Неизвестные  примем за базисные, а неизвестное
примем за базисные, а неизвестное  за свободное. Перенесём члены со свободными неизвестными в правые части уравнений последней системы:
за свободное. Перенесём члены со свободными неизвестными в правые части уравнений последней системы:  Отсюда имеем
Отсюда имеем  Приняв обозначения
Приняв обозначения  , получаем совокупность всех решений данной системы в виде:
, получаем совокупность всех решений данной системы в виде:
 ◄
◄
II. Задачи для индивидуальных заданий.
Задача 1.Вычислить определитель четвёртого порядка:
1. 
| 2. 
| 3. 
|
4. 
| 5. 
| 6. 
|
7. 
| 8. 
| 9. 
|
10. 
| 11. 
| 12. 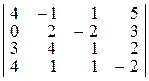
|
13. 
| 14. 
| 15. 
|
16. 
| 17. 
| 18. 
|
19. 
| 20. 
| 21. 
|
22. 
| 23. 
| 24. 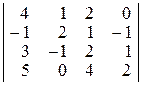
|
25. 
| 26. 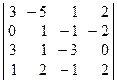
| 27. 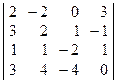
|
28. 
| 29. 
| 30. 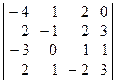
|
Задача 2.Даны две матрицы: А и В. Найти матрицы: а)  ; б)
; б)  ; в)
; в)  ; г)
; г)  ; д)
; д)  из уравнения
из уравнения  .
.
| Матрица А | Матрица В | Матрица А | Матрица В | ||
| 1. | 
| 
| 2. | 
| 
|
| 3. | 
| 
| 4. | 
| 
|
| 5. | 
| 
| 6. | 
| 
|
| 7. | 
| 
| 8. | 
| 
|
| 9. | 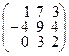
| 
| 
| 
| |
| 11. | 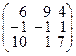
| 
| 12. | 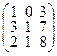
| 
|
| 13. | 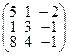
| 
| 14. | 
| 
|
| 15. | 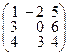
| 
| 16. | 
| 
|
| 17. | 
| 
| 18. | 
| 
|
| 19. | 
| 
| 20. | 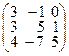
| 
|
| 21. | 
| 
| 22. | 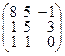
| 
|
| 23. | 
| 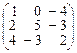
| 24. | 
| 
|

| 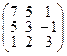
| 
| 
| ||

| 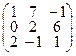
| 
| 
| ||

| 
| 
| 
|
Задача 3.1.Доказать, что данная система крамеровская и найти её решение по формулам Крамера.
1. 
| 2. 
| 3. 
|
4. 
| 5. 
| 6. 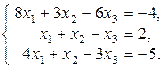
|
7. 
| 8. 
| 9. 
|
10. 
| 11. 
| 12. 
|
13. 
| 14. 
| 15. 
|
16. 
| 17. 
| 18. 
|
19. 
| 20. 
| 21. 
|
22. 
| 23. 
| 24. 
|
25. 
| 26. 
| 27. 
|
28. 
| 29. 
| 30. 
|
Задача 3.2.Методом Гаусса решить систему линейных уравнений, заданную расширенной матрицей. Обозначения неизвестных выбрать самостоятельно.
| 1. | 
| 2. | 
|
| 3. | 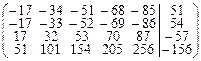
| 4. | 
|
| 5. | 
| 6. | 
|
| 7. | 
| 8. | 
|
| 9. | 
| 10. | 
|
| 11. | 
| 12. | 
|
| 13. | 
| 14. | 
|
| 15. | 
| 16. | 
|
| 17. | 
| 18. | 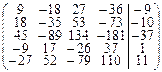
|
| 19. | 
| 20. | 
|
| 21. | 
| 22. | 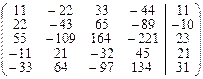
|
| 23. | 
| 24. | 
|
| 25. | 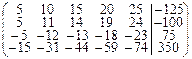
| 26. | 
|
| 27. | 
| 28. | 
|
| 29. | 
| 30. | 
|
Задача 3.3.Решить однородные системы линейных уравнений.
| 1. | А)  б)
б) 
| 2. | а)  б)
б) 
|
| 3. | А)  б)
б) 
| 4. | а)  б)
б) 
|
| 5. | А)  б)
б) 
| 6. | а) 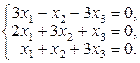 б)
б) 
|
| 7. | а)  б)
б) 
| 8. | а)  б)
б) 
|
| 9. | а) 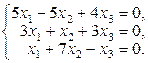 б)
б) 
| 10. | а) 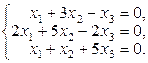 б)
б) 
|
| 11. | а)  б)
б) 
| 12. | а) 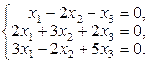 б)
б) 
|
| 13. | а)  б)
б) 
| 14. | а)  б)
б) 
|
| 15. | а)  б)
б) 
| 16. | а)  б)
б) 
|
| 17. | а)  б)
б) 
| 18. | а)  б)
б) 
|
| 19. | а) 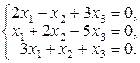 б)
б) 
| 20. | а)  б)
б) 
|
| 21. | а)  б)
б) 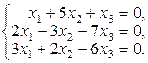
| 22. | а)  б)
б) 
|
| 23. | а)  б)
б) 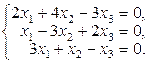
| 24. | а)  б)
б) 
|
| 25. | а)  б)
б) 
| 26. | а)  б)
б) 
|
| 27. | а)  б)
б) 
| 28. | а)  б)
б) 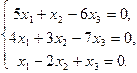
|
| 29. | а)  б)
б) 
| 30. | а)  б)
б) 
|
|
из
5.00
|
Обсуждение в статье: Системы линейных уравнений |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

