Определители четвертого порядка

Методы их вычисления

Определение. Выражение

называется определителем четвертого порядка. Этот определитель можно записать в виде:

, (6)

где - минор элемента, стоящего на пересечении i-ой строки и j-го столбца, -алгебраическое дополнение этого элемента.

Формулу (6) можно записать с помощью значка суммирования :

, (7)

где i=1,2,3,4.

Формула (7) называется разложением определителя по элементам

i-ой строки. Можно записать и разложение определителя по элементам j-го столбца:

(8)

где j=1,2,3,4.

Метод понижения порядка определителя основан на обращении всех, кроме одного, элементов строки или столбца определителя в нуль с помощью свойств определителей.

Пример 11.Вычислить определитель

.

Решение. Прибавим элементы первой строки к элементам второй строки:

.

Элементы первой строки умножим на (-2) и прибавим к элементам третьей строки:

.

Элементы первой строки умножим на (-1) и прибавим к элементам четвертой строки:

.

Разложим полученный определитель по элементам первого столбца

Переставим первые две строки, при этом знак определителя изменится на противоположный, одновременно вынесем общий множитель 3 элементов третьего столбца за знак определителя:

.

Умножим элементы первой строки на (-2) и прибавим к элементам второй строки:

.

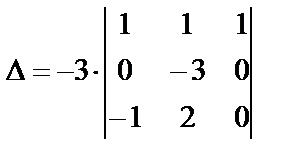Полученный определитель разложим по элементам второй строки

Пример 12. Вычислить определитель .

 Внимание!!! ошибка после 2 действия: при умножении 1 строки на (-2) и прибавлении к 4 строке получается 0 1 -3 2.

Решение. Поменяем местами первую и вторую строки, при этом по свойству 2 знак определителя изменится на противоположный:

.

Сначала элементы первой строки умножим на (-2) и прибавим к элементам второй и четвертой строк, а затем элементы первой строки умножим на (-3) и прибавим к элементам третьей строки, получим:

.

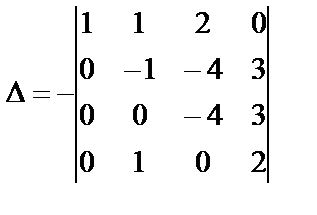Элементы второй строки прибавим к элементам четвертой строки:

.

Элементы третьей строки умножим на (-1) и прибавим к элементам четвертой строки:

.

Получим определитель треугольного вида, значение которого равно произведению элементов главной диагонали .

Пример 13. Вычислить определитель

.

Решение.Разложим определитель по элементам третьей строки

Полученные определители третьего порядка вычислим по правилу треугольника

Задания для самостоятельного решения.

1.Вычислить определители:

2. Решить уравнения:

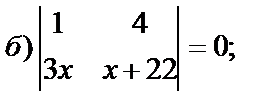
3. Решить неравенства:

4. Вычислить определители:

Ответы: 1. а)7; б)26; в)0; г)0; д)30. 2. а)5; б)2; в)2;

г) 3. а) б) в) г)[-1;7]. 4. а)-24; б)-40; в)-9; г)57; д)-5; е)1; ж)1; з)55; и)30; к)48; л)0; м)-1004; н)150.

Матрицы

Основные понятия

Определение. Матрицей называется прямоугольная таблица чисел, содержащая m строк одинаковой длины и n столбцов одинаковой длины, которая записывается в виде

(9)

или, сокращенно, , где , (т.е. ) – номер строки, (т.е. ) – номер столбца, числа называются элементами матрицы. Матрицу называют матрицей размера 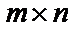и пишут . Например. , .

Определение. Две матрицы и равны между собой, если их размеры совпадают, а их соответствующие элементы равны, т.е. , если , где .

Например. Так как размеры матриц совпадают и соответствующие элементы равны, поэтому матрицы и равны, т.е.

Определение. Матрица, у которой число строк равно числу столбцов, называется квадратной. Квадратную матрицу размера называют матрицей n-го порядка.

Например. т.е. дана матрица второго порядка.

Определение. Квадратная матрица, у которой все элементы, кроме элементов главной диагонали, равны нулю, называются диагональной.

Матрица - диагональная.

Определение. Диагональная матрица, у которой каждый элемент главной диагонали равен единице, называется единичной. Обозначается буквой .

или .

Определение. Квадратная матрица называется треугольной, если все элементы, расположенные над главной диагональю (или под главной диагональю), равны нулю.

или - треугольные матрицы.

Важной характеристикой квадратной матрицы порядка n является ее определитель (или детерминант), который обозначается или . .

Определение. Квадратная матрица, у которой определитель отличен от нуля, т.е. , называется невырожденной. В противном случае матрица называется вырожденной.

Например,

Матрица А – вырожденная.

Матрица В – невырожденная.

Определение. Матрица, все элементы которой равны нулю, называется нулевой и обозначается буквой О.

В матричном исчисление матрицы О и Е играют роль чисел 0 и 1 в арифметике.

Определение. Матрица, содержащая одну строку, называется матрицей-строкой

Матрица, содержащая один столбец, называется матрицей-столбцом

Матрица размера , состоящая из одного числа, отождествляется с этим числом, т.е. есть 3.

Определение. Матрица, полученная из данной заменой каждой ее строки столбцом с тем же номером, называется матрицей транспонированной к данной. Обозначается .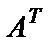

Если , то , если , то .

Транспонированная матрица обладает следующим свойством: .