Действия над матрицами

Определение. Суммой двух матриц и одинаковых размеров называется матрица того же размера такая, что

(10)

Пример 14.Найти сумму матриц и , если

Решение.

Для любых матриц и одинакового размера справедливы следующие свойства:

1.

2.

3. .

Определение. Произведением матрицы на число 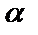называется матрица такая, что

(11)

Пример 15. , 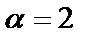. Найти .

Решение.

Матрица называется противоположной матрице .

Для любых матриц и одинакового размера и любых действительных чисел 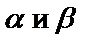справедливы следующие свойства:

1.

2.

3.

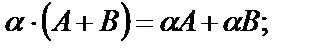
4.

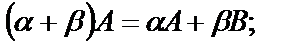
5. .

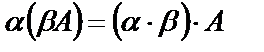Операция умножения двух матриц вводится только для случая, когда число столбцов первой матрицы равно числу строк второй матрицы.

Оределение.Произведением матрицы на матрицу называется матрица такая, что

, (12)

где , .

Формулу (12) для нахождения элемента полезно помнить в виде правила:

в матрице выделяем 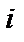- ю строку, в матрице выделяем -й столбец.

, .

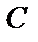Тогда для того, чтобы получить элемент матрицы , расположенный на пересечении i-й строки и k-го столбца, надо каждый элемент i-й строки матрицы умножить на соответствующий элемент k-го столбца матрицы и все полученные произведения сложить.

Если матрицы и квадратные одного размера, то произведения 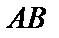и всегда существуют.

Пример 16. Найти произведение матриц и , если .

Решение. Для получения первой строки новой матрицы фиксируем в матрице первую строку (2 0), а в матрице выделяем поочередно первый, второй и третий столбцы: .

Элемент 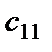находим как сумму произведений элементов первой строки матрицы на соответствующие элементы первого столбца матрицы по правилу: «произведение первого элемента строки на первый элемент столбца плюс произведение второго элемента строки на второй элемент столбца».

Пользуясь этим правилом, находим:

Для вычисления элементов , , фиксируем вторую строку матрицы (-1 3) и умножаем её поочередно на первый, второй и третий столбцы матрицы :

Пример 17. Даны матрицы

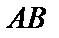Найти и .

Решение. Произведение 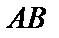не определено, так как число столбцов матрицы (3)не совпадает с числом строк матрицы (2). Произведение определено, так как число столбцов матрицы (2) совпадает с числом строк матрицы (2).

Используя правило, рассмотренное в предыдущем примере, найдем произведение :

Матрицы и называются перестановочными, если .

Умножение матриц обладает следующими свойствами:

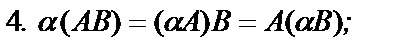
если указанные суммы и произведения матриц имеют смысл.

6. Если квадратная матрица n-го порядка, Е-единичная матрица того же порядка, то .

7. Для операции транспонирования верны следующие равенства:

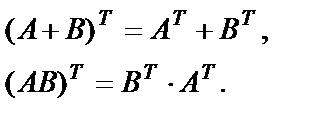
Пример 18. Даны матрицы

Проверить справедливость равенства 5.

Решение.Найдем произведение :

Таким образом,

Пример 19. Даны матрицы

Показать, что

Решение. Найдем произведение матриц АВ:

Найдем

Получим

Пример 20.Даны две матрицы

Найти АВ.

Решение.

Пример 21. Найти значение матричного многочлена если 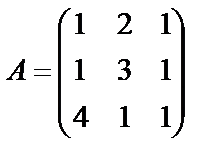, Е - единичная матрица третьего порядка.

Решение. . Найдем :

= ,

Пример 22. Найти произведение матриц , если оно определено, где

Решение.Рассмотрим матрицы и В. Размер матрицы , размер матрицы . Так как число столбцов матрицы (3) равно числу строк матрицы (3), то произведение определено, в результате получим матрицу размера .

Число столбцов матрицы (1) совпадает с числом строк матрицы 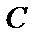(1), таким образом, произведение определено, получаемая матрица будет размера .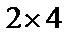

Найдем произведение :

Найдем произведение :

Обратная матрица

Пусть А-квадратная матрица n-го порядка

.

Определение. Матрица

составленная из алгебраических дополнений к элементам матрицы А, называется присоединенной к матрице А.

Алгебраические дополнения к элементам квадратной матрицы находятся так же, как к элементам ее определителя. В присоединенной матрице алгебраические дополнения элементов строки стоят в столбце с таким же номером.

Пример 23. Дана матрица

Найти матрицу, присоединенную к матрице А.

Решение. Найдем алгебраические дополнения к элементам матрицы А:

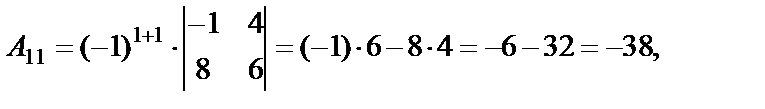
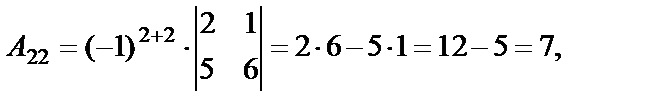
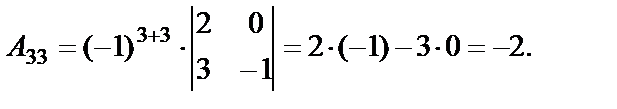
Составим матрицу , присоединенную к матрице А

.

Определение. Матрица называется обратной матрице А, если выполняется условие

, (14)

где – единичная матрица того же порядка, что и матрица . Матрица имеет те же размеры, что и матрица .

Теорема. Для того, чтобы матрица имела обратную матрицу, необходимо и достаточно, чтобы 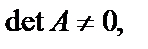то есть чтобы матрица была невырожденной.

Обратная матрица находится по формуле:

(15)

для матрицы А третьего порядка.

Свойства обратной матрицы:

1.

2.

3.

Пример 24. Найти , если

Решение. Проверим, является ли данная матрица невырожденной. Вычислим определитель, соответствующий матрице :

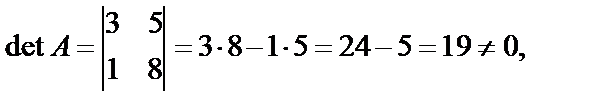следовательно, матрица невырожденная и для нее существует обратная матрица .

Найдем алгебраические дополнения элементов матрицы :

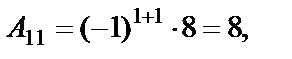
Составим матрицу по формуле (15)

Проверка:

Следовательно, обратная матрица найдена верно.

Пример 25. Показать, что матрица является обратной для , если

Решение. Найдем произведение матриц и :

Следовательно, матрица 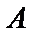является обратной для матрицы .

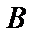Пример 26. Найти матрицу, обратную для матрицы

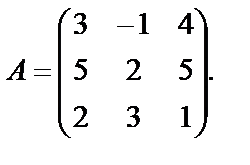
Решение. Найдем определитель матрицы :

Матрица – вырожденная, значит обратная для нее матрица не существует.

 

Пример 27. Найти матрицу, обратную для данной матрицы

Решение. Найдем определитель матрицы :

значит матрица невырожденнаяи для нее существует обратная матрица .

 

Вычислим алгебраические дополнения элементов матрицы :

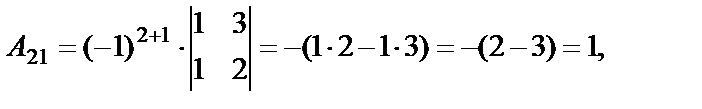
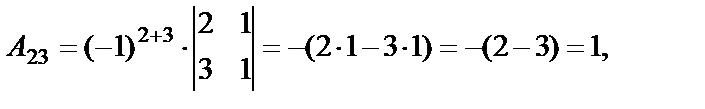
Используя формулу (15), составим матрицу :

.

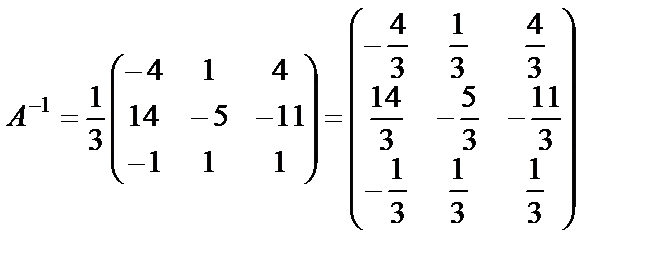Проверка:

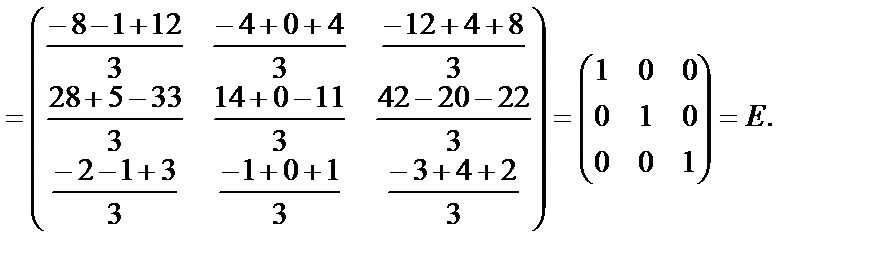
Значит обратная матрица найдена верно.

Ранг матрицы

Рассмотрим матрицу размера

.

Выделим в ней k строк и k столбцов 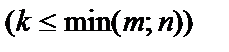. Из элементов, стоящих на пересечении выделенных строк и столбцов, составим определитель k-го порядка. Все такие определители называются минорами этой матрицы.

Определение. Рангом матрицы называется наибольший из порядков миноров данной матрицы, отличных от нуля.

Обозначают ранг матрицы или .

Пример 28. Найти ранг матрицы:

Решение. Дана матрица размера . Возможный ранг матрицы равен трем, т.к. . Но матрица содержит два нулевых столбца, поэтому все определители третьего порядка, составленные из элементов данной матрицы равны нулю:

, , .

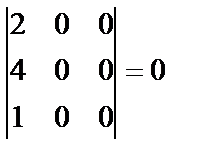Составим минор второго порядка, например

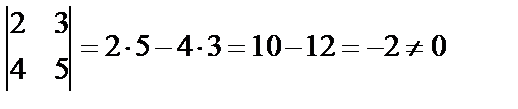. Значит,

Ранг матрицы удобно вычислять, используя элементарные преобразования над матрицей. К элементарным относятся следующие преобразования:

1) перестановка местами двух параллельных рядов матрицы;

2) умножение всех элементов ряда матрицы на число, отличное от нуля;

3) прибавление ко всем элементам ряда матрицы соответствующих элементов параллельного ряда, умноженных на одно и то же число.

Определение. Две матрицы и 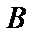называются эквивалентными, если одна из них получается из другой с помощью элементарных преобразований. Записывается ~В.

Свойства ранга матрицы:

1. При транспонировании матрицы ее ранг не меняется.

2. Ранг матрицы не изменится, если вычеркнуть из матрицы нулевой ряд.

3. При элементарных преобразованиях ранг матрицы не изменяется, т.е. если ~В, то

Пример 29. Найти ранг матрицы

Решение. Умножим элементы первой строки на (-2) и прибавим к элементам третьей строки

~

Элементы второй строки умножим на 3 и прибавим к элементам третьей строки

~

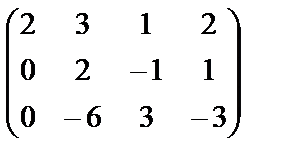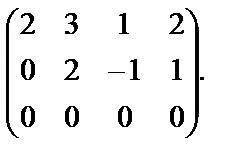
Вычеркнем третью строку полученной матрицы, т.к. все ее элементы равны нулю:

~ .

Составим минор второго порядка:

.

Таким образом,

В преобразованной матрице получилось две ненулевые строки.

Пример 30. Найти ранг матрицы

.

Решение. Умножим элементы первой строки на (-2) и прибавим к элементам второй строки данной матрицы:

~ .

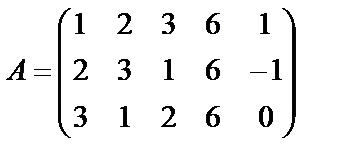Умножим элементы первой строки на (-3) и прибавим к элементам третьей строки:

~ .

Элементы второй строки полученной матрицы умножим на (-5) и прибавим к элементам третьей строки:

~

Из элементов полученной матрицы составим определитель третьего порядка. Для этого возьмем первые три столбца:

.

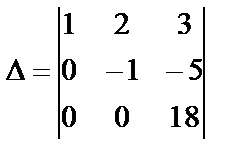Получили определитель треугольного вида, значение которого равно произведению элементов главной диагонали

.

Ранг последней матрицы равен 3, следовательно, ранг данной матрицы тоже равен 3.

В последней матрице содержится три ненулевые строки.

Можно сделать следующий вывод:

ранг матрицы равен количеству ненулевых строк преобразованной к треугольному виду матрицы.