Матричный метод решения систем

Рассмотрим систему n линейных уравнений с n неизвестными

(21)

Основная матрица системы .

Обозначим , 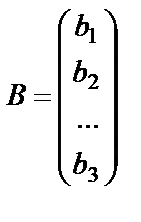. Пусть 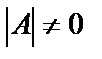, то есть матрица А невырожденная. Тогда систему (21) можно представить в виде уравнения

(22)

которое называется матричным уравнением. Решим матричное уравнение. Умножим обе части уравнения (22) слева на . Получим , а так как 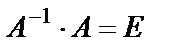, , тогда

(23)

Равенство (23) называется решением матричного уравнения (22).

Таким образом, чтобы решить систему уравнений (21) матричным методом, где 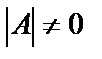, надо найти матрицу, обратную матрице А, и умножить ее на матрицу-столбец В, состоящую из свободных членов системы (21).

Пример 34. Решить систему уравнений матричным методом

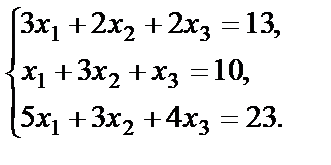
Решение. Выпишем основную матрицу системы

Проверим, является ли матрица А невырожденной:

значит матрица является невырожденной, поэтому обратная матрица к матрице существует и данную систему уравнений можно решить матричным методом.

Найдем алгебраические дополнения элементов матрицы :

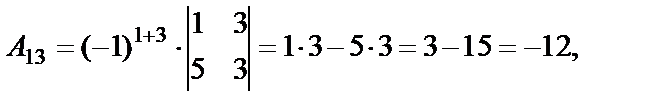
Составим матрицу , присоединенную к матрице А:

По формуле (15) получим матрицу , обратную к матрице А:

Найдем решение данной системы уравнений по формуле (23)

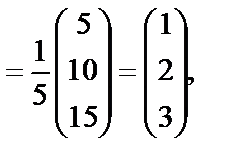то есть

Пример 35. Матричным методом решить систему уравнений

Решение. Запишем основную матрицу системы :

и вычислим определитель этой матрицы

В полученном определителе элементы первой строки пропорциональны соответствующим элементам второй строки, тогда по свойству 6 определителей

Матрица является вырожденной, а значит решить матричным методом данную систему невозможно.

Решение систем линейных уравнений по формулам Крамера

Пусть дана система n линейных уравнений с n неизвестными

определитель основной матрицы которой отличен от нуля, то есть система уравнений невырожденная.

Обозначим . Определитель получается из определителя путем замены элементов первого столбца столбцом из свободных членов:

.

Тогда .

Аналогично , где получен из путем замены элементов второго столбца столбцом из свободных членов;

, и так далее, .

Формулы

(24)

называются формулами Крамера.

Таким образом, невырожденная система n линейных уравнений с n неизвестными имеет единственное решение, которое может быть найдено матричным методом (23) или по формулам Крамера (24).

Пример 36. Решить систему уравнений по формулам Крамера

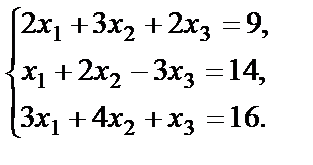
Решение. Составим и вычислим определитель данной системы уравнений

Данная система является невырожденной, поэтому ее решение можно найти по формулам Крамера (24).

Вычислим и :

Значит, , , .