Полную группу можно определить так: если

для любой пары (i¹j), тогда

{A₁,A₂, … ,A_n} - полная группа событий.

Самостоятельная работа

Тема «Основные понятия и определения теории вероятностей»

Законспектировать самостоятельно:

Учебник: Ниворожкина Л.И. Морозова З.А. Теория вероятностей и математическая статистика. - М.: Эксмо, 2009, 432 с.:

глава 4, стр.66-68; §4.2, стр.71-73; §4.1, стр.68-71.

глава 3, §3.1-3.7, стр.57-65

или по

Ниворожкина Л.И., Морозова З.А. Математическая статистика с элементами теории вероятностей в задачах с решениями:Учебное пособие. – Москва: ИКЦ «Март», 2005. – 600 с.: стр.58-65, стр.71-77.

 

Тема «Комбинаторика. Классификация событий. Классическое и статистическое определение вероятности».

Решение задач из: Ниворожкина Л.И., Морозова З.А. Математическая статистика с элементами теории вероятностей в задачах с решениями. Издательский центр «Март». – М., Ростов-на-Дону, 2005 - 600 с.:

№№ 2.2, 2.3, 2.4, 2.5, 2.7, 2.13, 2.14, 2.18, 2.24, 2.27, 2.31.

 

№№ 3.2, 3.3, 3.4, 3.5, 3.8, 3.9, 3.10

Тема 2. «Основные теоремы теории

Вероятностей.

Формулы полной вероятности и Байеса»

План темы

1. Основные теоремы (правила) сложения вероятно-

стей совместных и несовместных событий.

2. Свойства вероятностей событий, образующих

полную группу. Противоположные события.

3. Зависимые и независимые события.

4. Теоремы умножения вероятностей.

5. Независимость и зависимость событий в

совокупности.

6. Вероятность наступления хотя бы одного события

из независимых и зависимых событий в

совокупности.

7. Формулы полной вероятности и Байеса

 

Основные теоремы (правила) сложения вероятностей совместных и несовместных событий

Вероятность суммы двух событий А, В равна сумме вероятностей этих событий без вероятности их совместного наступления, то есть:

Р (А+В) = Р(А) + Р(В) - Р(АВ) (4)

или

Для несовместных событийих совместное наступление есть невозможное событие Æ, а вероятность его равна нулю. Следовательно, для несовместных событий правило сложения вероятностей принимает следующий вид:

Вероятность суммы двух несовместных событий равна сумме вероятностей этих событий.

Для несовместных событий A, B:
или 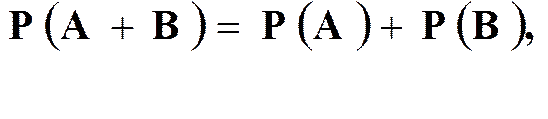Правило сложения вероятностей справедливо и для конечного числа n попарно несовместных событий, то есть:	(5)

P(A₁+A₂+A₃+...+A_n)=P(A₁)+P(A₂)+P(A₃)+...P(A_n)

или

 

В случае нескольких совместных событий необходимо по аналогии с рассуждениями о пересечении двух совместных событий исключить повторный учет областей пересечения событий. Рассмотрим три совместных события.

 

 

A		АВ В

АВС

АС ВС

С

 

 

Для случая трех совместных событий можно записать:

 

Р(А + В + С) = Р(А) + Р(В) + Р(С) - Р(АВ) - Р(АС) - Р(ВС) + +Р(АВС).

Сумма вероятностей событий А₁, А₂, А₃, ... , А_n,

образующих полную группу, равна 1, то есть:

P(A₁) + P(A₂) + P(A₃) + ... + P(A_n) = 1

или

(7)

 

Пример. В урне два белых и три черных шара. Чему равна вероятность появления белого шара при первом извлечении из урны? При втором извлечении из урны?

Здесь возможны два случая.

Первый случай. Схема возвращенного шара, то есть шар после первого испытания возвращается в урну.

Пусть событие А - “появление белого шара при первом испытании”. Так как N = 5, а М = 2, то Р(А) = 2/5.

Пусть событие В - “появление белого шара при втором извлечении”. Так как шар после первого испытания возвратился в урну, то N = 5, а М = 2 и Р(В) = 2/5.

Таким образом, вероятность каждого из событий не зависит от того, произошло или не произошло другое событие. События А и В в этом случае называются независимыми.

СобытияА, В называются независимыми, если вероятность каждого из них не зависит от того, произошло или нет другое событие.

Вероятности независимых событий называются безусловными.

Второй случай. Схема невозвращенного шара, то есть шар после первого испытания в урну не возвращается.

Вероятность появления белого шара при первом испытании Р(А) = 2/5. Белый шар в урну не возвращается, следовательно, в урне остались один белый и три черных шара.

Чему равна вероятность события В при условии, что событие А произошло? N = 4, M = 1.

Искомую вероятность обозначают Р(В/А) или Р(В)_А или Р_А(В). Итак, Р(В/А)=1/4 называют условной вероятностью, а события А, В называются зависимыми.

СобытияА, В называются зависимыми, если вероятность каждого из них зависит от того произошло или нет другое событие. Вероятность события В, вычисленная в предположении, что другое событие А уже осуществилось, называется условной вероятностью.

Очевидно, что если два событияА и В - независимые, то справедливы равенства:

Р(В) = Р(В/А), Р(А) = Р(А/В), или Р(В/А) - Р(В) = 0(8)

Вероятность произведения двух независимых событий А и В равна произведению их вероятностей:

P(AB) = P(A) ×P(B),
P(A B) = P(A) ×P(B)	(8)

 

Вероятность произведения двух зависимых событий А и В равна произведению вероятности одного из них на условную вероятность другого:

Р(АВ) = P(B) × Р(А/В)	(9)
Р(А В) = P(B) × Р(А/В)
или Р(АВ) = P(A)×Р(В/А)
Р(А В) = Р(A)×(В/А)
Вероятность события В при условии появления события А:
P(B/A) = или P(B/A) =	(10)
.

Распространим теоремы умножения на случаи n независимых и зависимых в совокупности событий.

События А₁, А₂, ..., A_n (n > 2) называются независимыми в совокупности, если вероятность каждого из них не зависит от того, произошли или нет любые события из числа остальных.

Вероятность совместного появления нескольких событий, независимых в совокупности, равна произведению вероятностей этих событий.

P(A₁ ×A₂×A₃×…×A_n) = P(A₁) ×P(A₂) × P(A₃) ×…×P(A_n) (11)

 

 

Вероятность совместного наступления конечного числа n зависимых событий равна произведению вероятности одного из них на условные вероятности всех остальных, причем условная вероятность каждого последующего события вычисляется в предположении, что все предыдущие уже наступили, т.е.

P(A1×A2×A3 ×... ×Аn) = Р(A1)×P(A2 / A1)×P(A3 / A1×A2).× . . .×P(An / A1×A2×A3×…×An-1) (12)

Если события А₁, А₂, ... A_n - зависимые в совокупности, то вероятность наступления хотя бы одного из них соответственно равна:

(13)

Вероятность появления хотя бы одного события из n независимых в совокупности, равна разности между 1 и произведением вероятностей событий, противоположных данным, то есть:

(14)