ВИДЫ КОНСТРУКТОРСКИХ ДОКУМЕНТОВ

Виды лекальных кривых

Лекальными называют плоские кривые, вычерченные с помощью лекал по предварительно построенным точкам. К лекальным кривым относят: эллипс, параболу, гиперболу, циклоиду, синусоиду, эвольвенту окружности, спираль Архимеда и др.

Эллипспредставляет собой замкнутую плоскую кривую второго порядка. Она характеризуется тем, что сумма расстояний от любой ее точки до двух точек фокусов есть величина постоянная, равная большей оси эллипса. Построить эллипс можно несколькими способами. Например, можно построить эллипс по его большой АВ и малой CD осям (рис.8, а). На осях эллипса как на диаметрах строят две окружности, которые можно разделить радиусами на несколько частей. Через точки деления большой окружности проводят прямые, параллельные малой оси эллипса, а через точки деления малой окружности — прямые, параллельные большой оси эллипса. Точки пересечения этих прямых и являются точками эллипса.

Рис.8

Можно привести пример построения эллипса по двум сопряженным диаметрам (рис.8,б) MN и KL. Сопряженными два диаметра называют, если каждый из них делит пополам хорды, параллельные другому диаметру. На сопряженных диаметрах строят параллелограмм. Один из диаметров MN делят на равные части; на такие же части делят и стороны параллелограмма, параллельные другому диаметру, нумеруя их, как показано на чертеже. Из концов второго сопряженного диаметра KLчерез точки деления проводят лучи. В пересечении одноименных лучей получают точки эллипса.

Параболой называют незамкнутую кривую второго порядка, все точки которой равно удалены от одной точки - фокуса и от данной прямой – директрисы.

Если круговой конус рассечь плоскость Р, параллельной одной из его образующих, то в плоскости сечения получится парабола (рис.9).

Рис.9


На рис.9 парабола построена по заданной точке А, вершине В и оси BD. Через точки А и Е проведем горизонтальную и вертикальную прямые дo пересечения в точке С. Отрезки АС и ВС делим на одинаковое число частей. Через полученные точки вертикального отрезка проведем горизонтальные прямые, а точки деления горизонтального отрезка соединим с вершиной параболы - с точкой В. Пересечение прямых с одинаковой нумерацией дает ряд точек параболы, которые соединяем плавной кривой.

Рассмотрим пример построения параболы по ее вершине О и какой-либо точке В(рис.10, а). С этой целью строят прямоугольник ОABC и делят его стороны на равные части, из точек деления проводят лучи. В пересечении одноименных лучей получают точки параболы.

Можно привести пример построения параболы в виде кривой, касательной прямой с заданными на них точками А и В (рис.10, б). Стороны угла, образованного этими прямыми, делят на равные части и нумеруют точки деления.

Рис. 10

Одноименные точки соединяют прямыми. Параболу вычерчивают как огибающую этих прямых.

Гиперболой называют плоскую незамкнутую кривую второго порядка, состоящую из двух веток, концы которых удаляются в бесконечность, стремясь к своим асимптотам. Гипербола отличается тем, что каждая точка ее обладает особым свойством: разность ее расстояний от двух данных точек-фокусов есть величина постоянная, равная расстоянию между вершинами кривой. Если асимптоты гиперболы взаимно перпендикулярны, она называется равнобокой. Равнобокая гипербола широко применяется для построения различных диаграмм, когда задана своими координатами одна точка М (рис.11, в). В этом случае через заданную точку проводят линии АВ и KL параллельно координатным осям. Из полученных точек пересечения проводят линии, параллельные координатным осям. В их пересечении получают точки гиперболы.

Циклоидойназывают кривую линию, представляющую собой траекторию точки А при перекатывании окружности (рис.11). Для построения циклоиды от исходного положения точки А откладывают отрезок АА], отмечают промежуточное положение точки А. Так, в пересечении прямой, проходящей через точку 1, с окружностью, описанной из центра О₁,получают первую точку циклоиды. Соединяя плавной прямой построенные точки, получают циклоиду.

Рис.11

 

Синусоидой называют плоскую кривую, изображающую изменение синуса в зависимости от изменения его угла. Для построения синусоиды (рис. 12) нужно разделить окружность на равные части и на такое же количество равных частей разделить отрезок прямой АВ = 2лR. Из одноименных точек деления провести взаимно перпендикулярные линии, в пересечении которых получают точки, принадлежащие синусоиде.

Рис. 12

 

 

Эвольвентой называют плоскую кривую, являющуюся траекторией любой точки прямой линии, перекатываемой по окружности без скольжения. Построение эвольвенты выполняют в следующем порядке (рис. 13): окружность делят на равные части; проводят касательные к окружности, направленные в одну сторону и проходящие через каждую точку деления; на касательной, проведенной через последнюю точку деления окружности, откладывают отрезок, равный длине окружности 2лR, который делят на столько же равных частей. На первой касательной откладывают одно деление 2лR/n , на второй - два и т. д.
Полученные точки соединяют плавной кривой и получают эвольвенту окружности

Рис. 13

 

Гипербола. Если рассечь прямой и обратный конусы плоскостью, параллельной двум его образующим или в частном случае параллельно оси, то в плоскости сечения получится гипербола, состоящая из двух симметричных ветвей (рис.14).

Рис.14

Гиперболой(рис.14) называется плоская кривая, у которой разность расстояний от каждой ее точки до двух данных точек F1 и F2, называемых фокусами, есть величина постоянная и равная расстоянию между ее вершинами а и Ь, например SF1-SF2=ab.

У гиперболы две оси симметрии - действительная АВ и мнимая CD. Две прямые KL и K1L1 проходящие через центр О гиперболы и касающиеся ее ветвей в бесконечности, называются асимптотами.

Гиперболу можно построить по заданным вершинам а и b и фокусам F1 и F2. Вершины гиперболы определяем, вписывая прямоугольник в окружность, построенную на фокусном расстоянии (отрезке F1F2), как на диаметре. На действительной оси АВ справа от фокуса F2 намечаем Произвольные точки 1, 2, 3, 4,... Из фокусов F1 и F2 проводим дуги окружностей сначала радиусом а-1, затем радиусом Ь-1 до взаимного пересечения по обе стороны от действительной оси гиперболы. Далее выполним взаимное пересечение следующей пары дуг радиусами а-2 и Ь-2 (точка S) и т. д. Полученные точки пересечения дуг принадлежат правой ветви гиперболы. Точки левой ветви будут симметричны построенным точкам относительно мнимой оси CD.

Рис.15

Вычерчивание лекальных кривых. Лекальные кривые строят по точкам, которые соединяют с помощью лекал. Предварительно от руки прорисовывают кривую по точкам. Принцип соединения отдельных точек кривой заключается в следующем. Выбираем ту часть дуги лекала, которая лучше всего совпадает с наибольшим количеством точек очерчиваемой кривой. Далее проводим не всю дугу кривой, совпадающую с лекалом, а лишь среднюю часть ее. После этого подбираем другую часть лекала, но так, чтобы эта часть касалась примерно одной трети проведенной кривой и не менее двух последующих точек кривой, и т. д. Таким образом, обеспечивается плавный

 

Методы проецирования:

 

Центральное проецирование:

пусть в пространстве задана плоскость П1, которую будем называть

плоскостью проекций.

Выберем какую-либо точку S, не лежащую на плоскости проекций.

Эту точку будем называть центром проецирования.

Заданную точку А пространства будем проецировать на плоскость

проекций П1. Для этого через точку А из центра проекций S проведем пря-

мую l. Эта прямая будет называться проецирующим лучем. Затем нахо-

дим точку пересечения А1 проецирующего луча SA с плоскостью проек-

ций П1. Точка А1 будет называться проекцией точки А (рис. 16а). Аналогич-

но выполним построение проекции В1 -точки В.

а б

Рис.16

 

Очевидно, что каждой точке пространства будет однозначно соот-

ветствовать своя собственная проекция. Однако на рис.16 б, мы видим, что

проекцией точки А и точки С является точка пересечения их общей про-

ецирующей прямой с плоскостью проекций.

Следовательно, такое изображение не является взаимно однознач-

ным, и судить о положении точек А и С в пространстве по одной проекции

нельзя, потому что одним из требований, предъявляемых к чертежам, явля-

ется точное определение положения пространственного объекта по его проекциям

 

Параллельное проецирование:

 

если центр проецирования S∞ удален в бесконечность , то

проецирующие лучи станут параллельны друг другу. Такое проецирование

называется параллельным.

Параллельное проецирование будет называться косоугольным, если проецирующие лучи не перпендикулярны к плоскости проекций и ортогональным, если проецирующие лучи перпендикулярны к плоскости проекций.

 

Параллельное косоугольное проецирование:

 

при этом проецировании задается направление и проецирующие лучи проводятся параллельно заданному направлению.

Для того чтобы спроецировать точку А на плоскость П1, надо провести проецирующий луч параллельно заданному направлению до пересечения с плоскостью проецирования П1, получим А1–проекцию точки А на плоскость П1.

Через точку А параллельно заданному направлению в пространстве

можно провести только одну прямую, следовательно, каждая точка про-

странства имеет одну и только одну параллельную проекцию.

Точки А и В принадлежат одному и тому же проецирующему лучу,

параллельному направлению s (рис. 17). Поэтому проекции этих точек В1

и А1 совпадают. Отсюда следует, что по одной заданной проекции положе-

ние в пространстве точек В и А определить невозможно.

 

Рис.17

 

Параллельное ортогональное (прямоугольное) проецирование:

 

ортогональное (прямоугольное) проецирование является частным

случаем параллельного проецирования, при котором направление про-

ецирования s выбирается перпендикулярным плоскости проекций П11 т.е.

s ⊥ П1

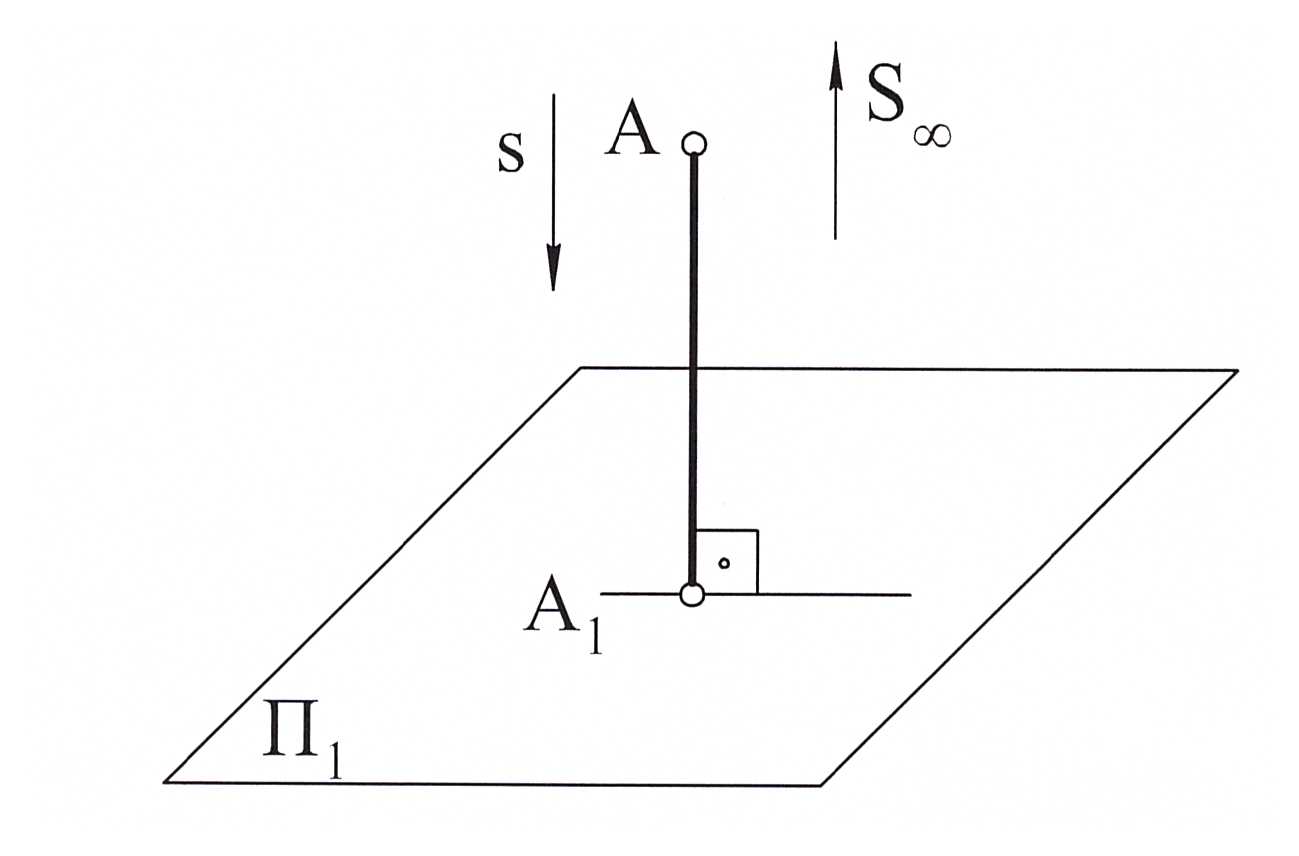
Рис.18

 

Такое проецирование является наиболее простым и удобным из всех

других существующих видов проецирования. Оно обеспечивает простоту

определения проекций геометрических объектов, а также позволяет сохра-

нить на проекциях их форму и размеры.

Прямоугольное проецирование имеет те же недостатки, что и цен-

тральное и параллельное проецирование: одна прямоугольная проекция не

дает возможности определить положение геометрического объекта в про-

странстве, надо иметь хотя бы две связанные между собой прямоугольные проекции.

 

Проекции точки:

проецирование будем вести на три взаимно перпендикулярные плос-

кости (рис.4):

П1 – горизонтальная плоскость проекций;

П1 – фронтальная плоскость проекций;

П3 – профильная плоскость проекций.

Линии пересечения этих плоскостей называют осями проекций (ко-

ординатными):

ОХ – ось абсцисс;

ОУ – ось ординат;

ОZ – ось аппликат

 

и рассматривают как систему прямоугольных декартовых координат с цен-

тром О.

Положение точки в пространстве определяется тремя координатами:

А (X, Y, Z).

Для получения прямоугольных проекций точки А необходимо из

этой точки опустить перпендикуляры на плоскости проекций. Основания

перпендикуляров и будут являться проекциями данной точки:

А1 – горизонтальная проекция точки;

А2 – фронтальная проекция точки;

А3 – профильная проекция точки.

Для получения более удобного чертежа необходимо совместить

плоскости проекций П1 и П3 вместе с изображением на них данной точки А

с плоскостью проекций П2 поворотом их вокруг осей ОХ и ОZ в направле-

нии, указанном стрелкой (рис.16). Такой совмещенный чертеж называется

эпюром или комплексным чертежом (рис.17).

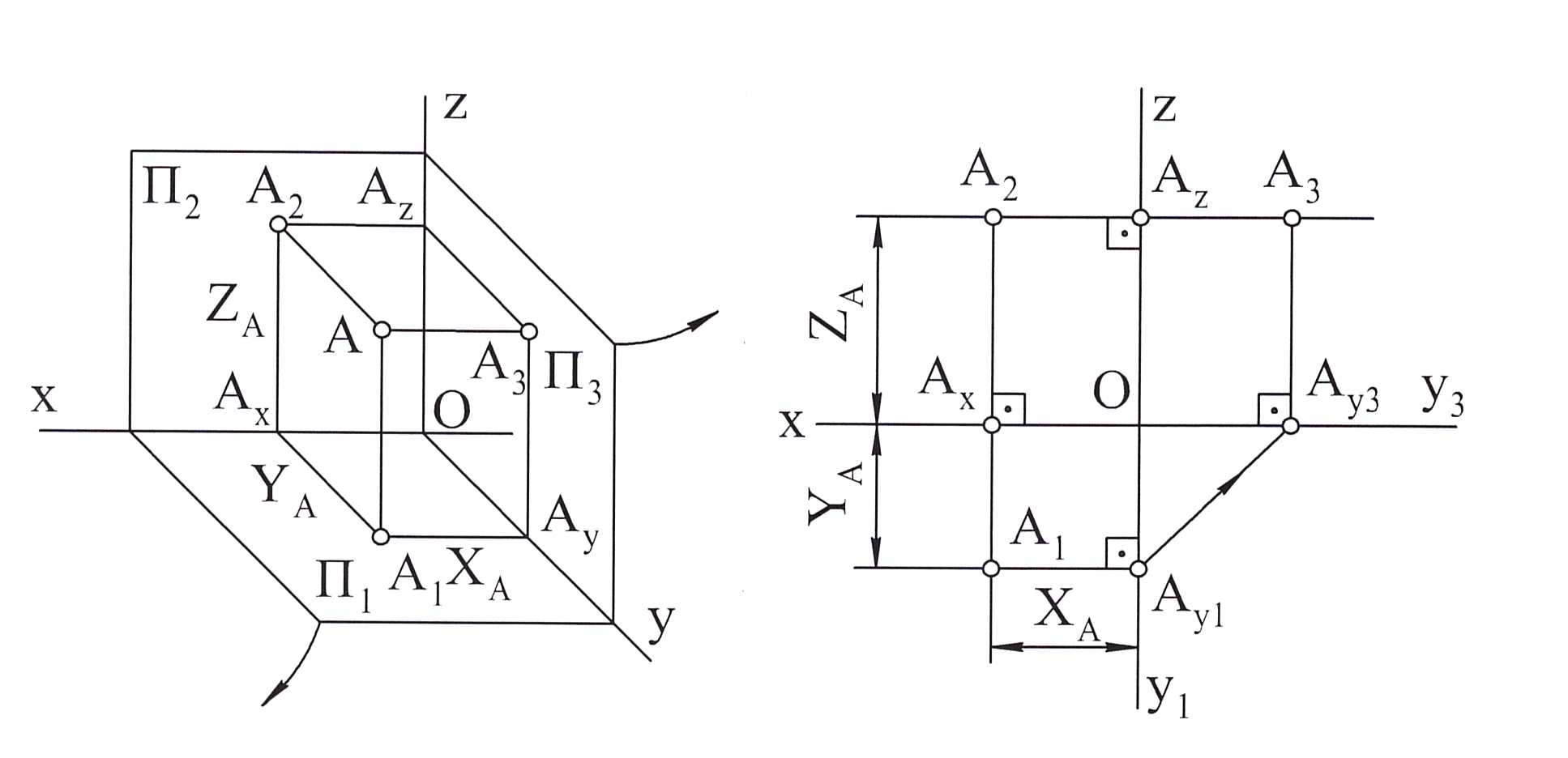
Рис.19 Рис.20

 

Из чертежа видно, что горизонтальная и фронтальная проекции точ-

ки лежат на одном перпендикуляре к оси ОХ, а фронтальная и профильная

проекции – на одном перпендикуляре к оси ОZ.

Прямая, которая соединяет на чертеже две проекции одной и той же

точки, называется линией связи.

А1А2 – всегда перпендикулярна оси ОХ;

2А3– всегда перпендикулярна оси ОZ.

 

Расстояния от заданной точки А до плоскостей проекций определя-

ются ее координатами:

⎥ АА3⎥ – абсцисса точки А (X);

⎥ АА2⎥ – ордината точки А (Y);

⎥ АА1⎥ – аппликата точки А (Z).

Каждая проекция точки определяется двумя координатами: А1 (X,

У); А2 (X, Z); А3 (У, Z), а две любые проекции определяются тремя коор-

динатами, следовательно, для задания точки достаточно двух проекций.

Если все три координаты точки отличны от нуля, точка находится в

пространстве (см. рис. 19 и рис. 20 и 21).

Если одна из координат равна нулю, точка находится в плоскости

проекций, например, точка В лежит в плоскости П1, поэтому координата

Z = 0 (рис. 1.8).

Если точка лежит на оси , то нулю равны две ее координаты (точка С

лежит на оси ОZ, см. рис. 18). Координаты Х и У равны 0.

Если все три координаты равны нулю, точка совпадает с началом ко-

ординат.

По двум известным проекциям всегда можно построить третью (рис. 1.9).

Рис. 21 Рис.22

 

 

Например, чтобы построить профильную проекцию А3 точки А по

данным горизонтальной А1 и фронтальной А2 проекциям, необходимо:

1) из точки А1 провести прямую, перпендикулярную ОУ, до пересе-

чения с ней в точке Ау1;

2) из точки Ау1 провести прямую под углом 45° к оси проекций ОУ1

до пересечения с осью ОУ3;

3) из полученной точки Ау3 восстановить перпендикуляр к оси ОУ3;

4) из фронтальной проекции А2 провести прямую, перпендикуляр-

ную оси ОZ, и продолжить ее до пересечения с построенной ранее

прямой из точки Ау3. На пересечении этих прямых находится ис-

комая проекция А3 точки А. Проекцию А3 можно найти так, как

показано на рис. 1.10, т.е. отложить от точки Аz отрезок, равный

координате У.

На рис. 24 построена горизонтальная проекция А1 точки А с помо-

щью постоянной прямой чертежа, когда известны фронтальная и профиль-

ная проекции точки А. Ее проводят под углом 45° к вертикальной или го-

ризонтальной линии связи (см. рис. 24).

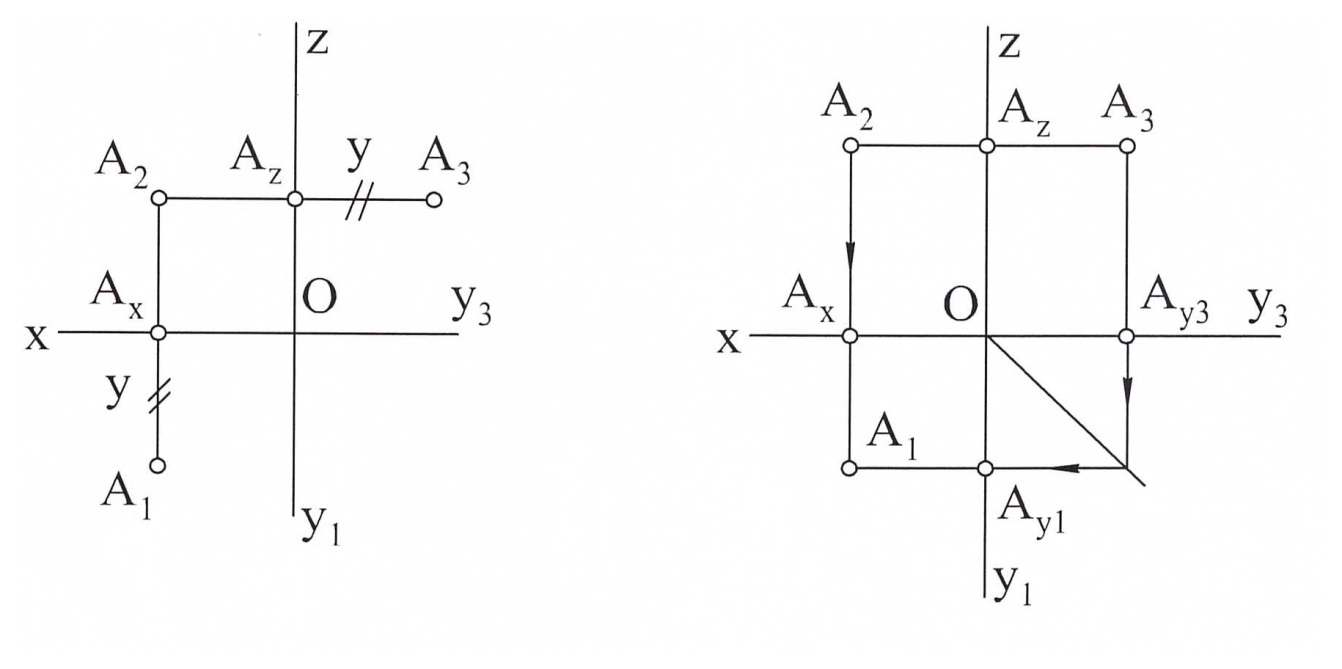
Рис. 23 Рис. 24

 

Часто для решения задач бывает достаточно иметь на чертеже только

две прямоугольные проекции предмета. В этом случае для получения чер-

тежа берут две взаимно перпендикулярные плоскости проекций – горизон-

тальную П1 и фронтальную П2.

Пересекаясь между собой, плоскости П1 и П2 делят пространство на

четыре части – 4 двугранных угла, которые называются четвертями. Их нумеруют в порядке указанном на рис. 25.

 

 

Рис. 25 Рис.26

 

Три плоскости проекций делят пространство на восемь октантов–8 трехгранных углов. Нумерация октантов дана на рис.26

 

Комплексный чертеж прямой линии

В соответствии со свойством прямолинейности параллельной проекции проекцией прямой линии является прямая линия. Поэтому на комплексном чертеже прямая линия будет задаваться в виде своих проекций – прямых линий. Как известно, прямая линия определяется двумя точками. Отсюда следует, что для построения проекций прямой достаточно взять на ней две произвольные точки (например, точки А и В) и спроецировать их ортогонально на горизонтальную и фронтальную плоскости проекций. Точки пересечения проецирующих лучей с плоскостями П1 и П2 определят проекции точек: горизонтальные – А1, В1 и фронтальные – А2 и В2. Соединив прямыми точки А1 и В1, получим горизонтальную проекцию прямой n, а точки А2 и В2 – фронтальную проекцию прямой n (рис.27). Таким образом, построение проекций прямой выполняется однозначно.

Рис.27

l.

Прямой общего положения называется прямая не параллельная и не перпендикулярная ни к одной из плоскостей проекций (рис.27). Прямые перпендикулярные или параллельные плоскостям проекций называются прямыми частного положения

 

Проекции плоских фигур

При проектировании плоских фигур, ограниченных прямыми линиями, достаточно спроектировать лишь вершины данной фигуры и затем последовательно соединить их одноименные проекции прямыми линиями; в результате получим проекции всех сторон фигуры, т. е. проекции данной фигуры.
Требуется спроектировать треугольник, заданный координатами вершин А,В и С. Спроектируем вершины А, В и С треугольника, как точки, получим их проекции А₁В₁С₁ и А₂В₂С₂ (рис.28,а). Соединим одноименные проекции точек прямыми, получим проекции А₁В₁, В₁С₁, С₁А₁ и А₂В₂,В₂С₂, С₂А₂ сторон треугольника, т.е. проекции A₁B₁C₁ и А₂В₂С₂ заданного треугольника (рис.28,б).

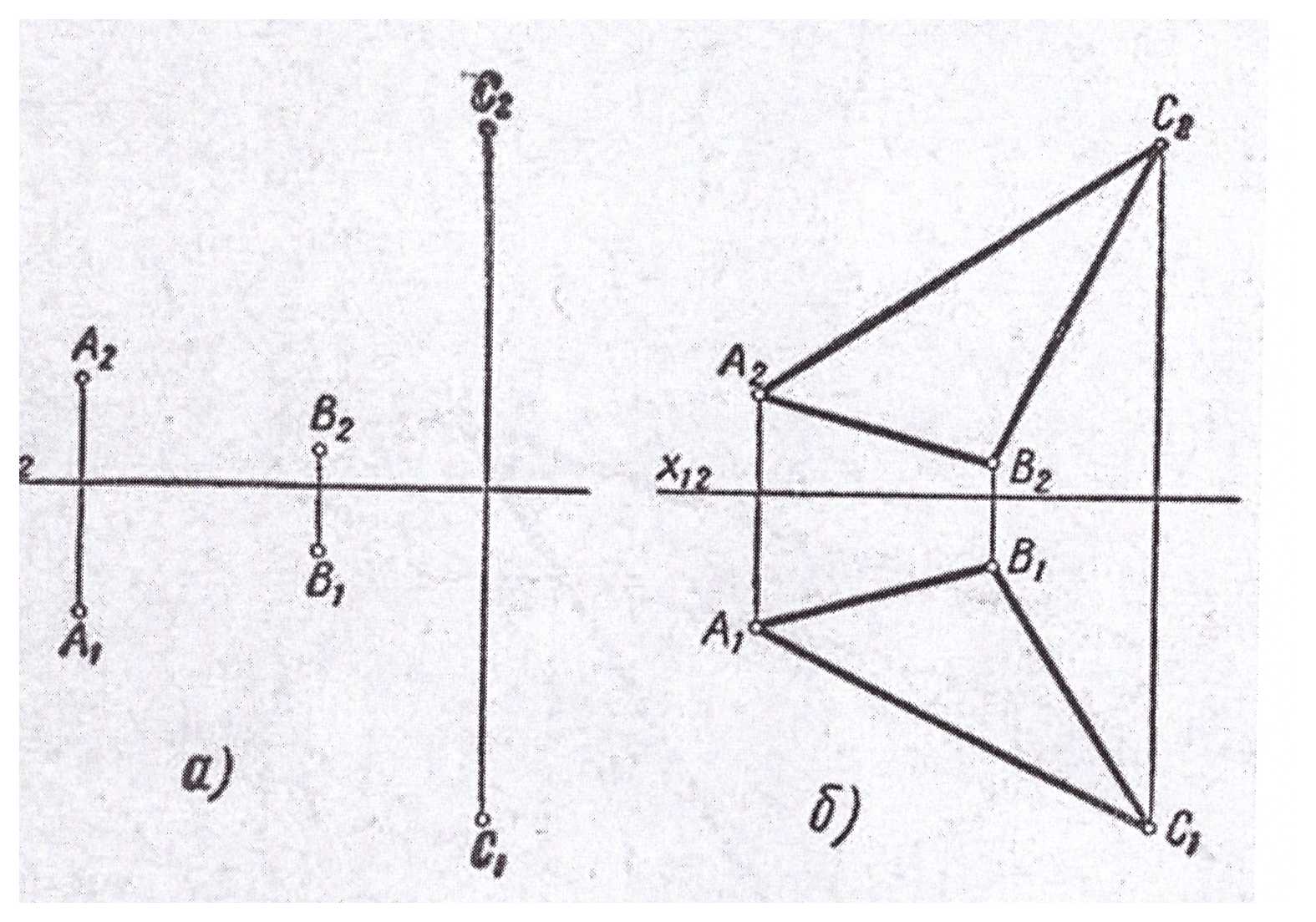
Рис.28

Рис.29

Треугольник всегда является плоской фигурой, чего нельзя сказать про четырехугольник, пятиугольник и т.д., плоскостность которых надо выявлять на чертеже.
Требуется спроектировать плоский четырехугольник ABCD (рис.29,а), заданный горизонтальной проекцией (А₁В₁С₁D₁) и фронтальной проекцией двух смежных сторон АВ и ВС (A₂B₂, В₂С₂)
Решение задачи сводится к нахождению фронтальной проекции вершины D(D₁,D₂).
Воспользуемся для данного случая двумя пересекающимися прямыми (диагоналями), определяющими плоскость фигуры четырехугольникаABCD.
Порядок построения фронтальной проекции показан цифрами:
1, 2 - провести горизонтальные проекции диагоналей B₁D₁ А₁С₁;
3 - провести фронтальную проекцию диагонали А₂С₂;
4 - найти фронтальную проекцию Е₂ (точки пересечения диагоналей);
5 - провести прямую через точки В₂ и E₂ (направление второй диагонали);
6 - найти фронтальную проекцию D₂ Найденную точку D₂ соединяем прямыми с одноименными проекциями вершин С и А (С₂ и А₂), получим недостающие проекции A₂D₂ и D₂С₂ сторон АО и ОС четырехугольника (рис.29,б). Четырехугольник ABCD плоский, так как его вершины лежат на пересекающихся прямых, которыми определяется плоскость.
Плоская фигура может занимать различные положения по отношению к плоскостям проекций:

Рис.30

а) быть параллельной одной из плоскостей проекций (рис.30,а);
б) быть перпендикулярной к одной из плоскостей проекций и наклонной к двум другим (рис.30,б);
в) быть наклонной к трем плоскостям проекций (рис.30,в);
г) лежать в одной из плоскостей проекций (рис.30,г).
В случае «а» фигура будет расположена в горизонтальной, фронтальной или профильной плоскостях. По свойству этих плоскостей одна из проекций равна натуральной величине проектируемой фигуры как лежащая в плоскости, параллельной плоскости проекций, а две другие проекции прямые, сливающиеся с проекциями плоскости, которая является двояко-проектирующей.
В данном случае горизонтальная проекция треугольника AВС (A₁B₁C₁) равна его натуральной величине. Фронтальная проекция - прямая, сливающаяся с проекцией λ₂ (рис.30,а).

В случае «б» фигура будет расположена в горизонтально-, фронтально- или профильно - проектирующих плоскостях. По свойству этих плоскостей одна из проекций явится прямой, сливающейся с соответствующей проекцией проектирующей плоскости; две другие проекции не представляют ее натуральной величины, так как фигура расположена в плоскости, находящейся под углом к плоскостям проекций.
Фронтальная проекция пятиугольника выявлена прямой, сливающейся с проекцией δ₂; горизонтальная проекция - фигура, не равная натуральной величине проектируемого пятиугольника (рис.30,б).
В случае «в» фигура будет расположена в плоскости общего положения, по свойству этой плоскости все проекции выявятся фигурами, не представляющими натуральной величины фигуры. Фронтальная, горизонтальная и профильная проекции — треугольники, не равные величине проектируемого треугольника (рис.30,в).
В случае «г» фигура будет расположена в плоскостях проекции П₁ или П₂, или П₃. Тогда одна из проекций будет сливаться с самой фигурой и равна ей; две другие проекции - прямые, сливающиеся с осями проекций, так как фигура расположена в плоскости проекций. Фронтальная проекция ромба сливается с ромбом; горизонтальная и профильная проекции сливаются с осями проекций х и у

 

Проекции тел

 

Рис.31

 

Проекции призмы

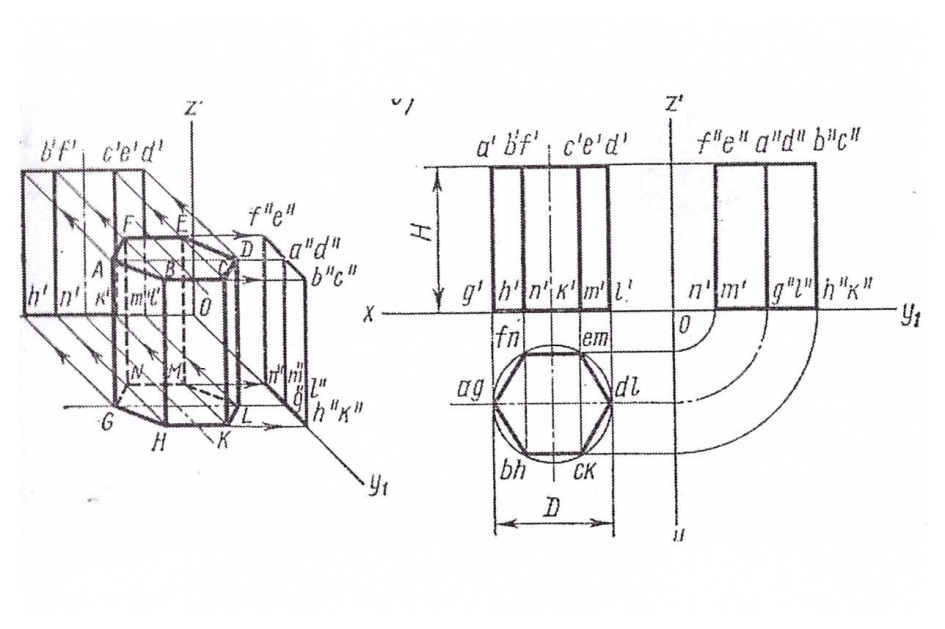
Рис.32

 

Проекции пирамиды

 

 

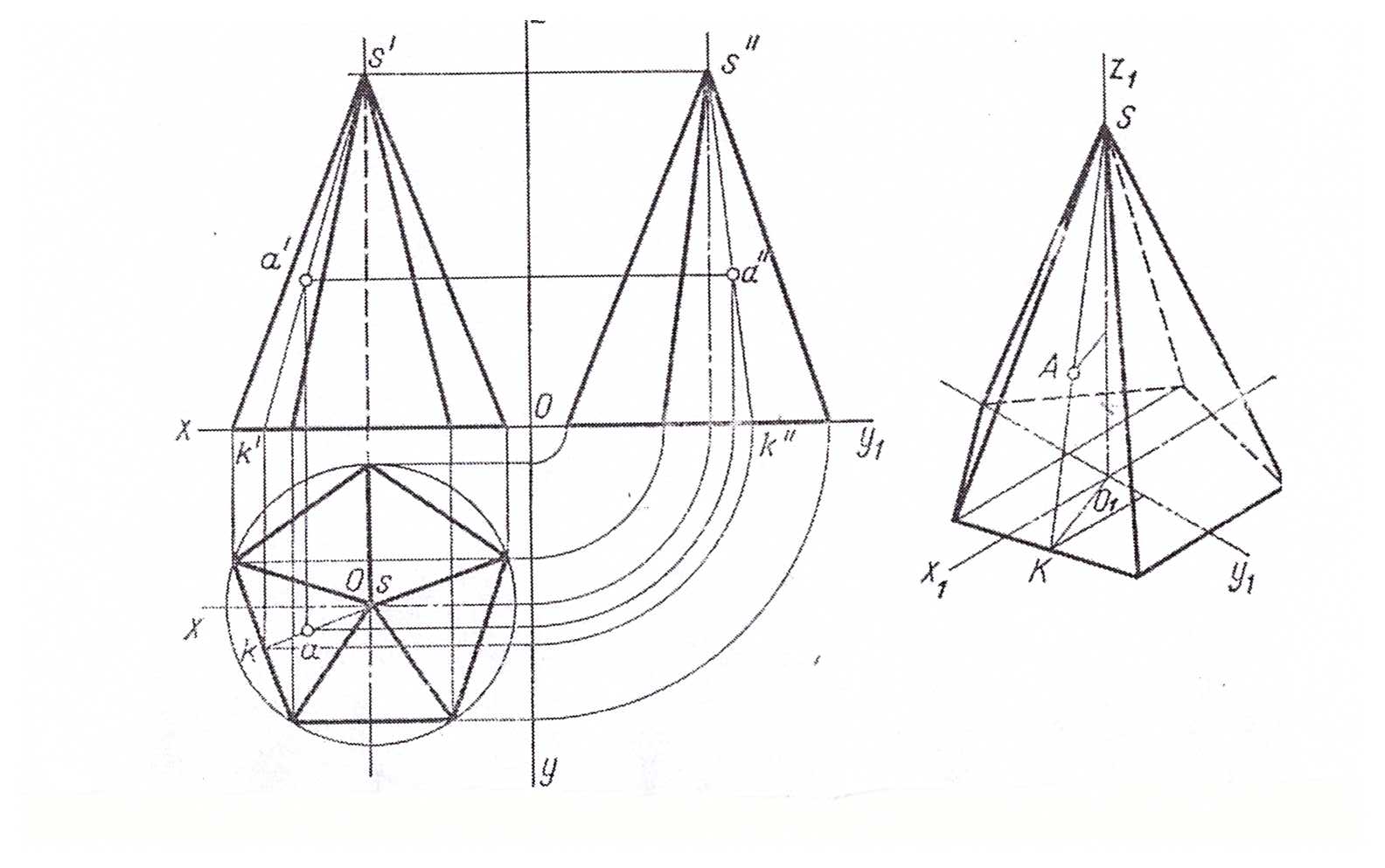
Рис.33

 

Пересечение пирамиды плоскостью

 

Рис.34

 

Проекции цилиндра

 

Рис.35

 

Пересечение цилиндра плоскостью

Рис.36

 

 

Проекции конуса

Рис.37

 

Проекции сферы

 

Рис.38

 

Развертки тел

 

 

Развертка призмы Развертка цилиндра

 

Рис.39

 

Развертка пирамиды Развертка конуса

Рис.40

 

ВИДЫ И СОСТАВ ИЗДЕЛИЙ

 

В соответствии с ГОСТ 2.101 - 68 изделиемназывается любой предмет или набор предметов производства, подлежащих изготовлению на предприятии. Изделия, в зависимости от их назначения, делят на изделия основного производства (изделия, предназначенные для реализации) и вспомогательного производства (изделия, предназначенные для собственных нужд предприятия).

В стандарте установлены следующие виды изделий:

· детали;

· сборочные единицы;

· комплексы;

· комплекты.

В зависимости от наличия или отсутствия составных частей изделия делят на:

а) неспецифицированные (детали) - не имеющие составных частей;

б) специфициpованные (сборочные единицы, комплексы, комплексы) -
состоящие из двух и более составных частей.

Структура изделий показана на рис. 1.

Рис. 41

Деталью называется изделие, изготовленное из однородного по наименованию и марке материала, без применения сборочных операций.

Сборочной единицей называется изделие, составные части которого соединяют между собой на предприятии посредством сборочных операций (свинчивание, клепка, сварка и т.п.), например: автомобиль, станок, маховичок из пластмассы с металлической арматурой.

Комплексом называются два и более специфициpованных изделия, не соединенных на предприятии-изготовителе сборочными операциями, но предназначенных для выполнения взаимосвязанных эксплуатационных функций, например: цех-автомат, корабль, бурильная установка.

Комплектом называются два и более изделий, не соединенных на предприятии-изготовителе сборочными операциями и представляющих собой набор изделий, которые имеют общее эксплуатационное назначение вспомогательного характера, например: комплект запасных частей, комплект инструмента и принадлежностей и т.д.

 

 

ВИДЫ КОНСТРУКТОРСКИХ ДОКУМЕНТОВ

 

Любые изделия могут быть изготовлены только на основании определённых конструкторских документов. К конструкторским документам относятся графические и текстовые документы, которые в отдельности или в совокупности определяют состав и устройство изделия и содержат необходимые данные для его разработки, изготовления, контроля, приёмки, эксплуатации и ремонта.

К графическим документам относятся различные виды чертежей, схем. В них содержится графическая информация об изделии.

Чертеж детали – документ, содержащий изображение детали и другие данные необходимые для ее изготовления и контроля.

Cбоpочный чертеж – документ, содержащий изображение сборочной единицы и другие данные, необходимые для ее сборки (изготовления) и контроля.

Чеpтёж общего вида – документ, определяющий конструкцию изделия, взаимодействие его составных частей и поясняющий принцип работы изделия.

Теоpетический чеpтёж – документ, определяющий геометрическую форму (обводы) изделия и координаты расположения составных частей.

Габаpитный чеpтёж – документ, содержащий контурное (упрощённое) изображение изделия с габаритными, установочными и присоединительными размерами.

Электpомонтажный, монтажный, упаковочный чеpтежи– документы, содержащие контурное (упрощённое) изображение изделия, а также данные, позволяющие производить указанную в названии операцию.

Cхема – документ, на котором показаны в виде условных изображений или обозначений составные части изделия и связи между ними.

Текстовыми конструкторскими документами являются документы, содержащие информацию об изделии в виде текстов, которые могут быть представлены в форме таблиц, перечней и т.п.

К текстовым документам относятся:

· спецификация;

· технические условия.

Спецификация –документ, определяющий состав сборочной единицы, комплекса или комплекта.

Технические условия – документ, содержащий требования к изделию, его изготовлению, контролю, приёмке и поставке, которые нецелесообразно указывать в других документах.