Теплопроводность. Механизмы теплопроводности в газах, жидкостях, твердых телах. Плотность теплового потока. Закон Фурье. Температуропроводность

Теплопроводность — это молекулярный перенос теплоты между непосредственно соприкасающимися телами или частицами одного тела с различной температурой, при котором происходит обмен энергией движения структурных частиц (молекул, атомов, свободных электронов).

Теплопроводность определяется тепловым движением микрочастиц тела. В чистом виде явление теплопроводности наблюдается в твердых телах, неподвижных газах и жидкостях при условии невозможности возникновения в них конвективных токов.

Передача теплоты теплопроводностью связана с наличием разности температур тела. Совокупность значений температур всех точек тела в данный момент времени называется температурным полем. В общем случае уравнение температурного поля имеет вид:

,

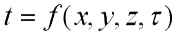где t — температура тела; х, у, z — координаты точки; τ — время.

 

Механизмы теплопроводности в газах, жидкостях, твердых телах.

 

Беспорядочность теплового движения молекул газа, непрерывные соударения между ними приводят к постоянному перемешиванию частиц и изменению их скоростей и энергий. В газе имеет место теплопроводность тогда, когда в нем существует разность температур, вызванная какими-либо внешними причинами. Молекулы газа в разных местах его объема имеют разные средние кинетические энергии. Поэтому при хаотическом тепловом движении молекул происходит направленный перенос энергии. Молекулы, попавшие из нагретых частей газа в более холодные, отдают избыток своей энергии окружающим частицам. Наоборот, медленно движущиеся молекулы, попадая из холодных частей в более горячие, увеличивают свою энергию за счет соударений с молекулами, обладающими большими скоростями.

 

Теплопроводность в жидкостях, как и в газах, имеет место при наличии градиента температуры. Однако если в газах передача энергии осуществляется при столкновениях частиц, совершающих поступательные движения, то в жидкостях энергия переносится в процессе столкновений колеблющихся частиц. Частицы, имеющие более высокую энергию, совершают колебания с большей амплитудой и при столкновениях с другими частицами как бы раскачивают их, передавая им энергию. Такой механизм передачи энергии, так же, как и механизм, действующий в газах, не обеспечивает ее быстрого переноса и поэтому теплопроводность жидкостей очень мала, хотя и превосходит в несколько раз теплопроводность газов. Исключение составляют жидкие металлы, коэффициенты теплопроводности которых близки к твердым металлам. Это объясняется тем, что в жидких металлах тепло переносится не только вместе с передачей колебаний от одних частиц к другим, но и с помощью подвижных электрически заряженных частиц – электронов, имеющихся в металлах, но отсутствующих в других жидкостях.

 

Если в твердом теле существует разность температур между различными его частями, то подобно тому, как это происходит в газах и жидкостях, тепло переносится от более нагретой к менее нагретой части.

В отличие от жидкостей и газов, в твердом теле не может возникнуть конвекция, т. е. перемещения массы вещества вместе с теплом. Поэтому перенос тепла в твердом теле осуществляется только теплопроводностью.

Механизм переноса тепла в твердом теле вытекает из характера тепловых движений в нем. Твердое тело представляет собой совокупность атомов, совершающих колебания. Но колебания эти не

независимы друг от друга. Колебания могут передаваться (со скоростью звука) от одних атомов к другим. При этом образуется волна, которая и переносит энергию колебаний. Таким распространением колебаний и осуществляется перенос тепла.

 

Приближенно вычисление коэффициента теплопроводности твердого тела, может быть выполнено с помощью квантовых представлений.

Квантовая теория позволяет сопоставить распространяющимся в твердом теле со скоростью звука колебаниям некоторые квазичастицы - фононы. Каждая частица характеризуется энергией, равной постоянной Планка умноженной на частоту колебания n. Энергия кванта колебаний - фонона, значит, равна hn.

Если пользоваться представлением о фононах, то можно сказать, что тепловые движения в твердом теле обусловлены именно ими, так что при абсолютном нуле фононы отсутствуют, а с повышением температуры их число возрастает, но не линейно, а по более сложному закону (при низких температурах пропорционально кубу температуры).

Твердое тело мы можем теперь рассматривать, как сосуд, содержащий газ из фононов, газ, который при очень высоких температурах может считаться идеальным газом. Как и в случае обычного газа перенос тепла в фононном газе осуществляется столкновениями фононов с атомами решетки, а все рассуждения для идеального газа справедливы и здесь. Поэтому коэффициент теплопроводности твердого тела может быть выражен совершенно такой же формулой

,

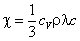где r - плотность тела, cV - его удельная теплоемкость, с – скорость звука в теле, l - средняя длина свободного пробега фононов.

В металлах помимо колебаний решетки, в переносе тепла участвуют и заряженные частицы – электроны, которые вместе с тем являются и носителями электрического тока в металле. При высоких температурах электронная часть теплопроводности много больше решеточной. Этим объясняется высокая теплопроводность металлов по сравнению с неметаллами, в которых фононы - единственные переносчики тепла. Коэффициент теплопроводности металлов можно подсчитывать по формуле:

,

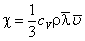где 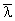- средняя длина свободного пробега электронов, 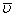- средняя скорость их теплового движения.

В сверхпроводниках, в которых электрический ток не встречает сопротивления, электронная теплопроводность практически отсутствует: электроны без сопротивления переносящие заряд, в переносе тепла не участвуют и теплопроводность в сверхпроводниках чисто решеточная.

 

 

Закон Фурье

Закон Фурье - основной закон распространения тепла теплопро­водностью, который вначале был известен как гипотеза Фурье, а позднее получил статус закона. Согласно этому закону количество тепло­ты dQ_τ , проходящее через элемент изотермической поверхности dF за промежуток времени dτ, пропорционально температурному градиенту ∂t/∂n:

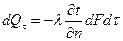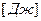, (7)

Коэффициент пропорциональности λ в уравнении (7) есть физический параметр вещества, который характеризует способность вещест­ва проводить теплоту и называется коэффициентом теплопроводности,

Количество теплоты, проходящей в единицу времени через изотер­мическую поверхность dF , называется тепловым потоком:

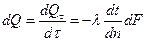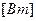, (8)

Количество теплоты, проходящее в единицу времени через единицу пути изотермической поверхности, называется плотностью теплового потока

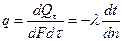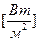, (9)

Плотность теплового потока является векторной величиной. За положительное направление вектора плотности теплового потока q принимают направление по нормали к изотермической поверхности в сторону убывания температуры. Таким образом, векторы q и gradt, лежат на одной прямой, но направлены в противоположные стороны, что и объясняет наличие знака "минус" в правых частях уравнений (7), (8) и (9).

Таким образом, уравнения (7), (8) и (9) представляют закон Фурье, записанный соответственно для всего тепла, для теплового потока и для плотности теплового потока.

Закон Фурье в интегральной форме запишется для всего тепла, прошедшего за время τ через изотермическую поверхность F:

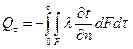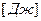, (10)

 

Для теплового потока

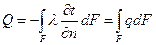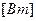, (11)

Если вектор плотности теплового потока спроектировать на ко­ординатные оси Ox, Oy, Oz , то согласно уравнению (6) получим:

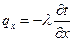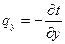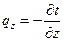, , . (12)

 

Температуропроводность (коэффициент температуропроводности) — физическая величина, характеризующая скорость изменения (выравнивания) температуры вещества в неравновесных тепловых процессах. Численно равна отношению теплопроводности к объёмной теплоёмкости при постоянном давлении, в системе СИ измеряется в м²/с.

,

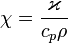где 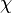— температуропроводность, 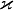— теплопроводность, 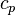— изобарная удельная теплоёмкость, ρ — плотность

Температуропроводность и теплопроводность являются двумя из наиболее важных параметров веществ и материалов, поскольку они описывают процесс переноса теплоты и изменение температуры в них.

Величина коэффициента температуропроводности зависит от природы вещества. Жидкости и газы обладают сравнительно малой температуропроводностью. Металлы, напротив, имеют бо́льший коэффициент температуропроводности.

 

2. Механизмы процесса кипения. Виды кипения - пузырьковое, пленочное.

Кипе́ние — процесс интенсивного парообразования, который происходит в жидкости, как на свободной её поверхности, так и внутри её структуры. При этом в объёме жидкости возникают границы разделения фаз, то есть на стенках сосуда образуются пузырьки, которые содержат воздух и насыщенный пар. Кипение, как и испарение, является одним из способов парообразования. В отличие от испарения, кипение может происходить лишь при определённой температуре и давлении. Температура, при которой происходит кипение жидкости, находящейся под постоянным давлением, называется температурой кипения. Как правило, температура кипения при нормальном атмосферном давлении приводится как одна из основных характеристик химически чистых веществ. Процессы кипения широко применяются в различных областях человеческой деятельности. Например, кипячение является одним из распространённых способов физической дезинфекции питьевой воды. Кипячение воды представляет собой процесс нагревания её до температуры кипения с целью получения кипятка.

Кипение является фазовым переходом первого рода. Кипение происходит гораздо более интенсивно, чем испарение с поверхности, из-за присутствия очагов парообразования, обусловленных как более высокой температурой достигаемой в процессе кипения, так и наличием примесей^[1].

На процесс образования пузырьков можно влиять с помощью давления, звуковых волн, ионизации и других факторов возникновения центров парообразования. В частности, именно на принципе вскипания микрообъёмов жидкости от ионизации при прохождении заряженных частиц работает пузырьковая камера.

В зависимости от плотности теплового потока, подводимого к жидкости от поверхности нагрева, на последней возникают отдельные паровые пузыри (пузырьковое кипение) или образуется сплошной слой пара (пленочное кипение). При пузырьковом кипении жидкость непосредственно омывает поверхность нагрева, причем ее пограничный слой интенсивно разрушается (турбулизуется) возникающими паровыми пузырями. Кроме того, всплывающие пузыри увлекают из пристенного слоя в ядро потока присоединенную массу перегретой жидкости, что создает интенсивный перенос теплоты от поверхности нагрева к общей массе кипящей жидкости. Следствием этого является высокая интенсивность теплоотдачи при пузырьковом кипении, возрастающая с увеличением числа действующих центров парообразования и количества образующегося пара.

При пленочном кипении жидкость отделена от поверхности нагрева слоем пара, с внешней стороны которого время от времени отрываются и всплывают крупные пузыри. Вследствие относительно малой теплопроводности парового слоя интенсивность теплоотдачи при пленочном кипении существенно меньше, чем при пузырьковом.

Возникновение того или иного вида кипения определяется плотностью теплового потока у поверхности нагрева, ее физическими свойствами (в частности смачиваемостью), физическими свойствами жидкости и гидродинамическим режимом потока в целом. Таким образом приходится говорить о существовании двух критических плотностях теплового потока. Первая критическая плотность теплового потока – при которой происходит переход от пузырькового кипения к пленочному, вторая – при которой происходит разрушение сплошного парового слоя и восстановление пузырькового режима кипения. В области значений плотности теплового потока, лежащих между двумя этими критическими значениями возможно устойчивое существование обоих режимов кипения или даже их длительное совместное сосуществование на разных частях одной и той же поверхности нагрева.

Паровая пленка обычно возникает в отдельных местах поверхности нагрева при достижении значений теплового потока выше критического и далее с конечной скоростью распространяется по всей поверхности нагрева. Аналогично при снижении теплового потока до значений меньше критического, происходят локальные разрушения пленки с последующим распространением пузырькового кипения на всю поверхность нагрева.

На поверхностях нагрева, обедненных центрами парообразования, процесс кипения имеет нестабильный характер, а интенсивность теплообмена колеблется между условиями конвекции однофазного потока и развитого пузырькового кипения. При этом возможен непосредственный переход от однофазной конвекции жидкости к режиму пленочного кипения.

Изучение условий, при которых возникают различные режимы кипения необходимо для расчета теплообменников, используемых в качестве испарителей. При появлении пленочного режима кипения эффективность работы испарителя падает и температура охлаждаемой среды на выходе из теплообменника оказывается выше заданной. Поэтому при расчете и подборе таких аппаратов очень важным является определение плотности тепловых потоков между двумя средами.

Механизм кипения

Характерной особенностью процесса кипения является образование паровой фазы. Основным параметром определяющим температуру пара (температуру насыщения) t_нac в пузыре при кипении является давление под которым находиться жидкость.

Температура кипящей жидкости обычно принимается равной температуре насыщения t_нac. Однако кипящая жидкость всегда несколько перегрета и ее температура t_ж выше температуры насыщения: t_ж-п = t_ж -t_нac . Например, при кипении при атмосферном давлении перегрев воды составляет t_ж-п = 0,4-0,8°С.

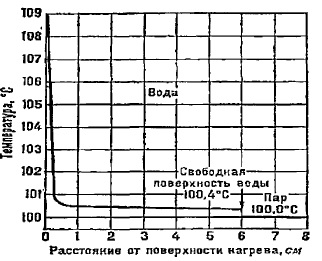
Известно, что в направлении к нагретой поверхности температура кипения жидкости почти постоянна. Однако, в слое толщиной 2-5 мм у поверхности нагрева наблюдается резкое возрастание температуры жидкости t_ж-п (рис. 1).

Рис. 1. Зависимость температуры кипящей воды от расстояния до поверхности нагрева

При пузырьковом кипении паровая фаза образуется в виде отдельных паровых пузырей, зарождающихся в определенных местах теплоотдающей поверхности или в массе кипящей жидкости. Для образования паровых пузырей необходимо наличие центров парообразования, которыми являются элементы шероховатости поверхности (микровпадины, микротрещины), микрочастицы и растворенные газы.

Во время роста паровой пузырь вытесняет жидкость, вызывает ее перемещение со скоростью, примерно равной скорости роста радиуса пузыря. После отрыва пузыря освободившееся пространство заполняется жидкостью, подтекающей к стенке из основного объема, и, когда она прогревается до температуры вскипания, у данного центра зарождается новый паровой пузырь.

С увеличением перегрева жидкости t_ж-п число действующих центров парообразования увеличивается и процесс кипения становится более интенсивным, что в основном обуславливается снижением влияния сил поверхностного натяжения, возникающих на границе раздела между жидкостью и паром

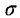₂ = 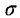₁ - K_c(t₂ - t₁), Н/м,

где 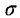₂ и 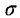₁ — поверхностное натяжение на границе вода-пар при температурахt₂ и t₁ ;

K_c ≈ 1,9-10^-3 Н/м·°С - коэффициент пропорциональности.

Давление пара в пузыре больше давления пара при испарении с плоской поверхности раздела фаз на суммарный перепад давления, обусловленный эффектами Лапласа и Томсона.

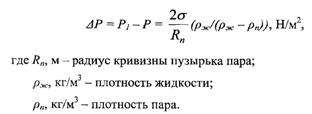
Учитывая что температура пара t_п в пузыре выше t_Hac, поскольку P₁ > Р и равна

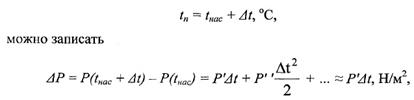
где P' — производная давления по температуре на линии насыщения, определяемая уравнением Клапейрона - Клаузиса

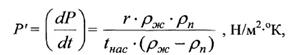
t_Hac, °К - абсолютная температура насыщения.

Поскольку при малых приращениях температуры приращения давления малы, производную dP/dt в уравнении Клапейрона - Клаузиуса можно представить отношением конечных разностей

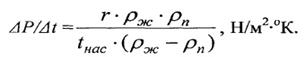
Подставив из (1) в (2) выразим минимальный начальный радиус пузыря, зарождающегося на центре парообразования, действующем при температурном напоре

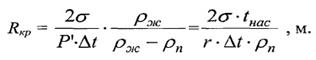
При этом для определения скорости роста парового пузыря обычно исходят из балансного соотношения массы испарившейся воды и приращения массы пара в пузыре за время dx.

В настоящее время можно выделить два основных подхода к определению скорости роста паровых пузырей.

Первый основан на предположении, что паровой пузырь растет в объеме равномерно перегретой жидкости, на испарение которой расходуется ее избыточная энтальпия.

Во второй физической модели, предложенной Д.А. Лабунцовым, предполагается, что в период роста пузыря теплота к нему подводится теплопроводностью через микропленку жидкости от теплоотдающеи поверхности.

По оценкам, в зависимости от свойств жидкости и геометрии пузыря, b₂ лежит в пределах 5< b₂<10.

Модель Д.А. Лабунцова получила дальнейшее развитие в работах, авторами которых было учтено, что испарение жидкости в паровой пузырь происходит не только с поверхности микропленки у основания пузыря, но и с остальной его поверхности.

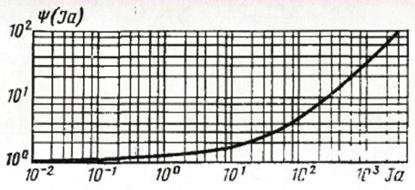
На рис. 2 представлены результаты расчета значений функции в зависимости от числа Ja (в интервале изменения последнего от 10^-2 до 10⁴) когда формула наилучшим образом согласуется с опытными данными.

Рис. 2. Зависимость от числа Ja

В реальных условиях кипения форма паровых пузырей обычно отличается от сферической и понятие отрывного радиуса парового пузыря R_om при его отделении от теплоотдающей поверхности в определенной мере является условным. Значением R_om характеризуется осредненный, то есть наиболее вероятный, радиус парового пузыря в момент отрыва. Замена действительной формы пузыря сферической значительно облегчает аналитический расчет и используется практически во всех теоретических исследованиях.

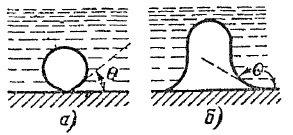
Если кипящая жидкость смачивает поверхность нагрева, то паровые пузырьки имеют тонкую ножку и легко отрываются (рис. 3а). Если кипящая жидкость не смачивает поверхность нагрева, то пар скапливается в пузыри с широкой ножкой (рис. 3б).

Рис. 3. Форма паровых пузырьков на смачиваемой (а) и несмачиваемой (б) поверхностях

Сочетания диаметра пузыря при отрыве и частоты его отрыва служат своеобразной мерой средней скорости роста паровых пузырей, поэтому комбинации 2R_om и f_om широко используются при теоретическом анализе процесса кипения и обобщении экспериментальных данных.

После отрыва от поверхности нагрева паровой пузырь за счет подъемной силы всплывает на поверхность жидкости, где разрушается с выделением пара в атмосферу.

Для определения затрат тепла на преобразование воды в пар, считаем что испарение воды происходит на одном центре парообразования только внутрь парового пузыря, при этом давление столба воды на паровой пузырь не учитываем. Тогда, количество тепла для образования одного парового пузыря определяется

Q_вп1 = Q₁ + Q₂ + Q₃ + Q₄, Дж,

где Q₁ Дж - количества тепла для расширения пара объемом V_пKp с избыточным давлением для создания парового пузыря минимального начального радиуса R_Kp.

 

Билет №4