Операции над множествами

Элементы математической логики

Методическая разработка по дисциплине ЕН.02 «Элементы математической логики» для обучающихся очной и заочной формы обучения специальности 09.02.03.Программирование в компьютерных системах

 

Псков 2018

 

Методическая разработка предназначена для обучающихся очной и заочной форм обучения по специальности Программирование в компьютерных системах при изучении предмета «Элементы математической логики»

Методическая разработка содержит лекционные материалы необходимые для изучения основных тем предмета, рекомендации по оформлению и выполнению домашней контрольной работы для заочного обучения, тексты контрольных работ.

Содержание методической разработки соответствует Государственному образовательному стандарту среднего профессионального образования по курсу «Элементы математической логики».

 

 

Оглавление

 

Введение 4

I. Элементы теории множеств

1. Основные понятия теории множеств 5

2. Операции над множествами 7

II. Логика высказываний

1. Понятие высказывания. Операции над высказываниями

2. Законы логики высказываний. Построение таблиц истинности для формул логики высказываний

3. Равносильные преобразования формул логики высказываний

4. Дизъюнктивные и конъюнктивные нормальные формы

5. Совершенная дизъюнктивная нормальная форма и совершенная конъюнктивная нормальная форма

III. Булевы функции

1. Понятие булевой функции

2. Свойства булевых функций

IV. Алгебра предикатов

1. Основные понятия

2. Операции над предикатами

3. Формулы логики предикатов

4. Равносильные формулы логики предикатов

V. Методические рекомендации по выполнению контрольной работы

1. Общие положения

2. Методические указания по оформлению контрольной работы

3. Варианты контрольной работы (1-30)

VI. Список литературы.

 

ВВЕДЕНИЕ

Логика образует такой пласт общечеловеческой культуры, без освоения которого в настоящее время не может состояться ни одна мыслящая личность. Математическая логика — вершина развития логики, достигнутая ею в XX в. Органично соединив в себе традиционную логику и методы современной математики, она получила столь глубокие и поразительные результаты, не принимать в расчет которые стало просто невозможно не только тем, кто изучает, преподает и творит математику, но и всем тем, для кого методы рассуждений, обоснований и доказательств являются главными методами деятельности. Результаты, полученные с помощью математической логики, легли в основу проектирования и создания электронно-вычислительных машин (компьютеров) и программного обеспечения к ним, нашли широчайшее применение в областях информатики и систем искусственного интеллекта.

Термин «логика» — наука о способах доказательств и опро-вержений — происходит от греческого слова - λογοζ (логос), что означает «слово», «понятие», «смысл». Математическая логика, называемая также символической или теоретической логикой, выросла из логики традиционной, но составила значительное её расширение. С одной стороны, эта наука применила математические методы для изучения общих структур (форм) правильного мышления и тем самым оформилась как раздел математики, с другой — математическая логика сделала предметом своего изучения процесс доказательства математических теорем и сами математические теории. Известный российский логик П. С. Порецкий точно подметил, что математическая логика по предмету своему есть логика, а по методу — математика.

Учебная дисциплина «Элементы математической логики» является общеобразовательной учебной дисциплиной в цикле математических и общих естественнонаучных дисциплин базовой части федерального компонента ОПОП СПО, которая обеспечивает общеобразовательный уровень подготовки специалиста и соответ-ствует развитию его профессионально значимых качеств.

Дисциплина «Элементы математической логики» базируется на общеобразовательной дисциплине «Математика». Материал дисциплины используется при изучении ряда дисциплин общего естественнонаучного цикла и профессионального цикла - «Теории алгоритмов», «Теории вероятности и математической статистики», «Основы программирования», «Математических

методов» и др.

I. ЭЛЕМЕНТЫ ТЕОРИИ МНОЖЕТВ

Основные понятия теории множеств

В фундаменте современных математических теорий лежат понятия множество, элементы множества, отношения принадлежности элемента множеству.

Интуитивный смысл этих понятий ясен: под множеством понимают совокупность некоторых объектов (которые называются элементами данного множества), мыслимых как единое целое.

Для обозначения того, что объект a является элементом множества А, пишут 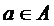(а принадлежит А),или запись 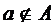(а не принадлежит А).

Наиболее распространены следующие два способа задания множеств:

1. перечисление элементов (используется в основном для множеств, состоящих из конечного числа элементов).

Примеры:

1. А = {1, 2, –5, 3} – множество А состоит из элементов 1, 2, –5, 3.

2. А = {1, {1}, a }множество А состоит из числа 1, одноэлементного множества {1}(содержащего единственный элемент – число 1) и буквы а.

2. выделение множества в другом множестве с помощью характеристическогосвойства его элементов: если В – множество и P(x) – некоторое свойство (высказывание о произвольном элементе 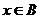), то можно определить новое множество А всех элементов x множества В, удовлетворяющих свойству P

Примеры:

1. { | x˃0 } - множество всех положительных действительных чисел.

2. А = { –1, 1} = {r Î R | r = 1} = { n Î Z | |n| = 1} - одно и то же множество можно задать различными способами.

Поэтому важно ввести понятие равенства двух множеств.

Два множества А и В называются равными (символически А = В), если они состоят из одних и тех же элементов.

Это значит, что для любого элемента а А выполнено а В, и для любого элемента b B выполняется b A. В противном случае множества А и В называются неравными: А В.

Множество А называют подмножеством множества В (говорят также, что А содержится в В или В содержит А) и записывают А В, если любой элемент множества А принадлежит множеству В.

Для удобства вводят в рассмотрение пустое множество Æ , не имеющее ни одного элемента.

Примеры:

1.{1, 2, 3} = {3, 1, 2}. Хотя порядки перечисления элементов этих множеств и различны, но каждый элемент одного множества является элементом другого множества, что и обеспечивает их равенство.

2.{1, 2, 3} = {1, 1, 2, 3, 2, 1, 3}. Второе множество, хотя и выглядит «толще» первого, но на самом деле состоит их тех же элементов.

3.{1, 2, 3}¹ {3, {1}, 2}. Элемент 1 первого множества не является элементом второго множества. Точно так же Элемент {1}второго множества не является элементом первого множества.( Кстати, почему 1 {1}?)

4.А = {1, 2}¹ {1, 2, –1} = В, т.к. –1 Î В, но –1 Ï А, но {1, 2}

{1, 2, –1}, т.к. 1 Î В и 2 Î В.

5.N = {1, 2, 3, …} Z = {… , –2, –1, 0, 1, 2, …} Q = { Î R |

m Î Z, n Î N} R .

Операции над множествами

I. Если А, В – множества, то существует множество А 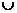В – объединение множеств А и В, которое состоит из всех элементов, являющихся элементами либо множества А, либо множества В: т.е.

x Î A È B « x Î A или x Î B.

Примеры:

1.Если A = {1, 2, 5, Æ}, B = {{1}, 2, 5, Æ}, то

АÈ В = {1, 2, 5, Æ,{1}}.

2.Если A = {x Î R | 1 < x £ 5}, B = {x Î R | –1 £ x < 2},

то A È B = [–1; 5], где [–1; 5] = {x Î R | –1 £ x £ 5}.

II. Если А, В – множества, то существует множество А 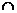В – пересечение множеств А и В, которое состоит из всех элементов, являющихся одновременно элементами и множества А, и множества В: т.е. x Î A Ç B « x Î A и x Î B.

Примеры:

1.Если A = {1, 2, 5, Æ}, B = {{1}, 2, 5, Æ}, то АÇ В = {2, 5, Æ}.

2.Если A = {x R| 1 < x 5}, B = {x R| –1 x < 2},

то A 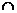B ={ (1; 2)}, где {(1; 2)} = {x R| 1 < x < 2}.

На основе понятий пересечения и объединения двух множеств можно ввести аналогичные операции над несколькими множествами:

A1Ç … Ç An = (…((A1Ç A2) Ç A3) Ç …) Ç An ,

A1È … È An = (…((A1È A2) È A3) È …) È An .

III.Если А, В – множества, то существует множество А \ В – разность множеств А и В, которое состоит из всех элементов, принадлежащих множеству А, но не принадлежащих множеству В: x Î A \ B « x Î A и x Ï B.

Примеры:

1.Если A = {1, 2, 5, Æ}, B = {{1}, 2, 5, Æ}, то А \ В = {1}.

2.Если A = {x Î R | 1 < x £ 5}, B = {x Î R | –1 £ x < 2},

то A \ B ={ [2; 5]}.

IV. Если А – множество, то существует множество всех его подмножеств B(A), называемое также булеаном множества А, и состоящее из всех подмножеств множества А: X Î B(A) « X Í A.

Важно отметить, что булеан B(A) состоит из множеств (подмножество множества А само является множеством) и содержит в качестве элементов пустое множество Æ и само множество А (которые в случае А = Æ совпадают).

Примеры:

1.Если А = Æ, то B(A) = {Æ}.

2.Если A = {1}, то B(А) = {Æ, {1}}.

3.Если A = {1, 2}, то B(А) = {Æ, {1}, {2}, {1, 2}}.

4.Если A = {1, 2, 3}, то B(А) = {Æ, {1}, {2}, {3}, {1, 2}, {1, 3}, {2, 3}, {1, 2, 3}}.

Можно доказать, что булеан n-элементного множества А состоит из 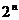элементов. Поэтому булеан часто называют степенью множества А и обозначают .

V. Если А, В – множества, то существует их прямое(декартово) произведение

А´В, состоящее из всех упорядоченных пар (a; b), где аÎ А, b Î B:

А´В = {(a; b) | a Î A , b Î B}.

Примеры:

1.Если А = {1}, B = {0, 5}, то А´В = {(1; 0), (1; 5)}.

2.Если А = {0, 2}, B = {0, 5}, то А´В = {(0; 0), (0; 5), (2; 0), (2; 5)}.

3.Если множество А состоит из m элементов, а множество В – из n элементов, то можно доказать, что множество А´В состоит из m´n элементов. По этой причине в названии множества А´В используется термин “произведение”. Если А = B, то множество А´А состоит из элементов и называется декартовым квадратом множества А и обозначается через .

Вслед за декартовым произведением двух можно ввести и декартово произведение

A1 ´ … ´ An = ( … ((A1 ´ A2) ´ A3)´ …)´ An) n множеств A1 , … , An . Множество A´...´ A, состоящее из n множителей А называется декартовой степенью множества A и обозначается .

Декартово произведение А´В = {(a; b) | a Î A Ù b Î B} двух множеств А и В иногда условно изображают на плоскости, трактуя компоненты упорядоченной пары (a; b) как координаты: a – координата по оси x, на которой отмечают множество А, а b – координата по оси y, на которой отмечают множество В. Таким образом, элементы (a; b) Î А´B условно изображаются точками на плоскости с “координатами” a и b.

Особенно удобно графическое изображение декартова произведения А´В в случае, когда А и В –числовые множества, т.е. АÍ R, B Í R . Тогда изображение принимает не условный характер, а имеет вполне конкретный геометрический смысл: множество А´В представляет из себя множество точек M(a; b) декартовой плоскости, первая координата а которых принадлежит множеству А, а вторая b – принадлежит множеству В.