 |
Главная |
ИЗОГНУТАЯ ОСЬ БАЛКИ. ОПРЕДЕЛЕНИЕ ПЕРЕМЕЩЕНИЙ В БАЛКАХ
|
из
5.00
|
Изгиб балки сопровождается искривлением её оси. При этом точки оси получают поперечные перемещения, или прогибы, а поперечные сечения балки поворачиваются относительно своих нейтральных осей. Углы поворота поперечных сечений принимаются равными углам наклона касательной к изогнутой оси балки. Прогибы и углы поворота в балках называют линейными и угловыми перемещениями.

Закон изменения прогиба оси балки.

где φ(х) – угол наклона касательной к изогнутой оси балки
Таким образом, прогиб является функцией координаты х.
Дифференциальное уравнение изогнутой оси балки.
Вид изогнутой оси балки определяется:
1) Действующей нагрузкой
2) Геометрическими характеристиками сечения (моментом инерции)
3) Материалом балки (модуль упругости материала)
Таким образом, прогиб балки является функцией трёх величин:
y= f(M, E, I)
M= f(x)
Поскольку, модуль упругости материала балки и момент инерции поперечного сечения от координаты х не зависят, то можем записать:
y= E·I·M(x)
При определении нормальных напряжений при изгибе рассматривалось три стороны задачи – геометрическая, физическая и статическая. В результате этого была получена зависимость (1):
 (1)
(1)
где р – это радиус кривизны изогнутой оси балки.
Так как в выражение (1) вошли все три фактора, то необходимо выразить 1/р через прогиб. Для этого воспользуемся выражением высшей математики(2):
 (2)
(2)
Выражение (2) – это точное дифференциальное уравнение оси изогнутой оси балки. Так как в реальных конструкциях нормами проектирования допускаются сравнительно малые прогибы, а именно в пределах от 1:200 до 1:1000 в пролётах, то изогнутая ось балки в реальности пологая, при этом угол порота балки φ<=1о (фото). Поскольку производная прогиба равна тангенсу угла наклона касательной к изогнутой оси. В связи с этим слагаемым yI2 можно пренебречь. Таким образом, получим, что (фото) (4). Изгибающий момент положителен, то есть М >0, когда растягиваются нижние волокна балки и балка обращается выпуклостью вниз. Вторая производная функции отрицательная, если кривая обращена выпуклостью в положительную сторону оси. Таким образом, при положительном изгибающем моменте вторая производная у должна быть отрицательной. Следовательно, в уравнении (4) удерживается знак – и формула принимает вид:
 (5).
(5).
Выражение (5) называется приближённым дифференциальным уравнением изогнутой оси балки.
Основные дифференциальные зависимости.
(фото)
Методы решения дифференциального уравнения изогнутой оси балки.
Существует три метода решения дифференциальных уравнений изогнутой оси балки.
1. Метод непосредственного интегрирования;
2. Метод начальных параметров;
3. Метод Мора.
Метод непосредственного интегрирования.
Этот метод заключается в непосредственном интегрировании уравнения (5). Зная закон изменения изгибающего момента по длине балки, можно определить функцию прогиба. Интегрирование ведётся по участкам, для которых должны быть известны аналитические выражения изгибающих моментов. В результате двукратного интегрирования, на каждом участке появляются две произвольные постоянные. Если балка разбивается на N участков, то постоянных интегрирования будет 2N. Эти постоянные интегрирования определяют из граничных условий и условий сопряжения участков.
Метод начальных параметров (метод академика Крылова)

В методе начальных параметров начало координат всегда располагается в крайней левой точке. Начальными параметрами называют 4 величины, а именно прогиб, угол поворота, изгибающий момент, и поперечная сила в начале координат. Дифференциальное уравнение изогнутой оси балки для произвольного сечения записывается в виде:

Дважды интегрируя уравнение (7), получим уравнение прогибов изогнутой оси балки. В общем виде для любого сочетания нагрузок, а также учитывая, что n! - это n!, обобщённое универсальное уравнение прогибов (не обращая внимания на знаки) запишется в виде (8).

ЗАМЕЧАНИЯ
· Начало координат всегда располагается в крайней левой точке;
· Перед началом расчёта прогибов и углов поворота необходимо определить реакции опор и учитывать их в уравнениях как внешние нагрузки;
· Знак слагаемого в уравнениях (8) и (9) противоположен знаку момента от этой нагрузки;
· При расчёте в уравнениях удерживаются только слагаемые, стоящие левее ограничителя участка;
· Начальные параметры определяются из граничных условий или условий на опорах
Типичные случаи граничных условий. 

В первом случае все начальные параметры известны, можно определить прогиб в любой точке балки.
Во втором случае неизвестен один параметр φ0. Он определяется из граничного условия на второй опоре. Для этого записывается уравнение прогиба для второй опоры, приравнивается к 0 и решается относительно единственного неизвестного φ0. После определения φ0 можно определить прогиб в любой точке балки.
В третьем случае неизвестно два параметра – у0 и φ0, которые определяются без дополнительных граничных условий на опорах. После их определения можно рассчитать прогиб в любой точке балки.
✓Лекция 07.03.18 «Определение перемещений методом Мора (энергетический метод определения перемещений)»
При определении перемещений методом Мора рассматривается равенство работы внешних и внутренних сил на вызванных ими перемещениях. Внешние силы, приложенные к телу, совершают работу … при этом в теле накапливается энергия деформации, т.е. потенциальная энергия. За счёт накопленной энергии при разгрузке тела происходи восстановление его первоначальных размеров.
Рассмотрим действие сосредоточенной силы, приложенной к консольной балке:

При нагружении балка изгибается и точки её оси получают поперечные перемещения, при этом сила P производит работу на перемещении Δ по направлению её действия. Если материал балки является линейно-упругим, то перемещение прямо пропорционально силе.
 , где k – это коэффициент пропорциональности, зависящий от свойств материала балки, от её размеров и формы поперечного сечения.
, где k – это коэффициент пропорциональности, зависящий от свойств материала балки, от её размеров и формы поперечного сечения.
 – работа силы (A) численно равна площади диаграммы (заштрихованного треугольника) на предыдущем рисунке (1, б).
– работа силы (A) численно равна площади диаграммы (заштрихованного треугольника) на предыдущем рисунке (1, б).
Каждому виду нагрузки соответствует своё перемещение: сосредоточенной силе соответствует линейное перемещение по направлению её действия, сосредоточенному моменту соответствует угловое перемещение или угол поворота поперечного сечения, в котором приложен момент.
Работу внешних сил, приложенных к балке можно выразить через внутренние усилия. В поперечных сечениях могут действовать три внутренних усилия:
1. Изгибающий момент
2. Поперечная сила
3. Продольная сила
Если вырезать из стержня бесконечно малый элемент, то в его торцевых сечениях действуют внутренние усилия:

Для каждого элемента внутренние усилия можно рассматривать как внешние нагрузки, производящие работу на соответствующих деформациях элемента.
Рассмотрим балку, находящуюся под действием произвольных нагрузок:

Состояние балки под действием заданных нагрузок называется грузовым или действительным. Допустим, требуется определить прогиб балки в некоторой точке C. Для определения этого прогиба, приложим в точку С по направлению искомого перемещения единичную силу, т.е. создадим единичное или вспомогательное состояние. Вырежем из балки бесконечно малый элемент и рассмотрим действующие в его торцевых сечениях внутренние усилия. При этом воспользуемся принципом независимости действия сил и вычислим, раздельно, работу каждого усилия. Обозначим как:
Qp, Np, Mp – внешние силы по отношению к элементу ds;
Q1, N1, M1 – внутренние силы по отношению к элементу ds;
P1 = 1
1. Продольные силы.Они вызывают взаимные осевые перемещения поперечных сечений, величина которых равна удлинению или укорочению элемента

Согласно закону Гука удлинение элемента определяется выражением:

Работа продольной силы N1 на этом удлинении равна:
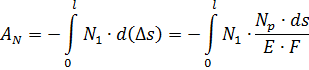
2. Изгибающие моменты вызывают взаимный поворот поперечных сечений элемента:
 , где точка O – центр кривизны, ρp – радиус кривизны оси балки под действием внешних нагрузок, dφp – угол взаимного поворота сечений под действием внешних нагрузок
, где точка O – центр кривизны, ρp – радиус кривизны оси балки под действием внешних нагрузок, dφp – угол взаимного поворота сечений под действием внешних нагрузок
Учитывая, что при изгибе балки его нейтральный слой сохраняет свою первоначальную длину и используя выражения для кривизны изогнутой оси балки (без учёта знака) имеем:  |·ds
|·ds
Умножим обе части этого выражения на ds и получим величину угла взаимного поворота сечений:

Работа момента M1 на угловом перемещении dφp, равна:

3. Поперечные силы. Они вызывают взаимный сдвиг поперечных сечений элемента:

dy – деформация сдвига.
Работа поперечной силы Q1на деформацию сдвига определяется по формуле:
 , где G – модуль упругости материала балки при сдвиге, k – безразмерный коэффициент, зависящий от формы сечения балки и учитывающий неравномерность касательных напряжений по высоте поперечного сечения:
, где G – модуль упругости материала балки при сдвиге, k – безразмерный коэффициент, зависящий от формы сечения балки и учитывающий неравномерность касательных напряжений по высоте поперечного сечения:
· для прямоугольного сечения 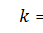
· для круглого сечения 
· для двутаврового сечения 
4. Работа внешней единичной силы:
 на перемещении
на перемещении 

Применив вариационный принцип Лагранжа, который гласит «Если упругая система находится в равновесии, то суммарная работа всех внешних и внутренних сил на любых малых возможных перемещениях равна нулю», получим:

(формула (9) называется формулой Мора)
Таким образом для определения, с помощью формулы Мора, перемещений в балке от действия заданных нагрузок, производится расчет системы и определяются усилия грузового состояния 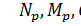 затем по направлению искомого перемещения прикладывается единичная сила или единичный момент и определяются внутренние усилия
затем по направлению искомого перемещения прикладывается единичная сила или единичный момент и определяются внутренние усилия  после чего выражения для усилий подставляются в формулу Мора и производится интегрирование в пределах длины стержня и суммирование результатов интегрирования по всем стержням системы.
после чего выражения для усилий подставляются в формулу Мора и производится интегрирование в пределах длины стержня и суммирование результатов интегрирования по всем стержням системы.
Если в результате вычислений величина Δip оказалась положительной, то направление перемещения совпадает с направлением действия единичной нагрузки, иначе – наоборот (не совпадает).
Для шарнирно-стержневых систем, стержни которых работают на растяжение или сжатие, например, для ферм, отлично от нуля только одно слагаемое формулы Мора:

При расчёте балок и стержневых систем, работающих, в основном, на изгиб, можно, с достаточной степенью точности, использовать только одно слагаемое:

✓Лекция 14.03.18 «Вычисление интеграла мора перемножением эпюр по правилу А.К. Верещагина. Часть 1»
|
из
5.00
|
Обсуждение в статье: ИЗОГНУТАЯ ОСЬ БАЛКИ. ОПРЕДЕЛЕНИЕ ПЕРЕМЕЩЕНИЙ В БАЛКАХ |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

