 |
Главная |
Способы решения иррациональных уравнений
|
из
5.00
|
Курсовая работа
по дисциплине элементарная математика
тема: «Методы и приемы решения иррациональных уравнений с параметром»
Выполнил студент 11 группы 1 курса _
Направление подготовки: Педагогическое образование
Профиль: математика и информатика
Агеева Екатерина Сергеевна
Научный руководитель:
ст. преподаватель Высоцкая П.А.
Дата защиты: «07» июня 2018г.
Оценка: ___________________________
_______________________________
(подпись научного руководителя)
Регистрационный номер ________
Дата регистрации ______________
Москва 2018
Оглавление
Введение. 3
§1. ИРРАЦИОНАЛЬНЫЕ УРАВНЕНИЯ.. 4
1.История возникновения. 4
2.Способы решения иррациональных уравнений. 5
3.Сущность решения задач с параметром. 13
4.Основы решения уравнений с параметром. 17
§ 2. ПРИМЕРЫ РЕШЕНИЯ ИРРАЦИОНАЛЬНЫХ УРАВНЕНИЙ С ПАРАМЕТРОМ 19
ЗАКЛЮЧЕНИЕ. 37
ЛИТЕРАТУРА.. 38
Введение
В школьном курсе алгебры мы рассматривалиразные виды уравнений: линейные, квадратные, кубические, уравнения с параметрами, иррациональные и множество других. Эта курсовая работа посвящена иррациональным уравнениям, которые содержат в себе параметр.
Изучение многочисленных физических и геометрических закономерностей зачастую приводит к решению уравнений, включающих параметр.
Задачи и уравнения, включающие параметр, развивают логическое мышление.
Трудности этого типа уравнений: множество формул и способов, применяемых при решении уравнений данного вида; возможность решения одного и того же уравнения, включающего параметр, разными методами.
Целью курсовой работы является изучение методов и приемов решения различных иррациональных уравнений, содержащих параметр.
Для достижения данной цели нам необходимо выделить следующие задачи:
1) Выявить основные положения теории решения иррациональных уравнений, содержащих параметр;
2) Классификация методов решения;
3) Разобрать примеры решения иррациональных уравнений с параметром
ИРРАЦИОНАЛЬНЫЕ УРАВНЕНИЯ
История возникновения
“Источником алгебраических иррациональностей является двузначность или многозначность задачи; ибо было бы невозможно выразить одним и тем же вычислением многие значения, удовлетворяющие одной и той же задаче, иначе, чем при помощи корней…; они же разве только в частных случаях могут быть сведены к рациональностям”.
(Лейбниц Г.)
Математики и астрономы Ближнего и Среднего Востока вслед за астрономами древнего Вавилона и эллинистической эпохи обширно использовали шестидесятеричные дроби, арифметические действия с которыми они именовали «арифметикой астрономов». Согласно аналогии с шестидесятеричными дробями самаркандский ученый XV в. ал-Каши в своей работе «Ключ арифметики» внедрил десятичные дроби, которые он применял с целью повышения точности извлечения корней. Вне зависимости от него, по такому же пути шел открывший в 1585 г. десятичные дроби в Европе Симон Стевин, который в собственных «приложениях к алгебре» (1594 г.) выявил, что десятичные дроби можно применять с целью бесконечно близкого приближения к действительному числу. Таким образом, уже в XVI в. зародилась концепция о том, что естественным аппаратом для введения и обоснования понятия иррационального числа являются десятичные дроби. Возникновение «Геометрии» Декарта облегчило понимание связи между измерением различных отрезков (и геометрических величин вообще) и необходимостью расширения определения рационального числа. В числовой оси иррациональные числа, равно как и рациональные, представляются точками. Данное геометрическое объяснение позволило лучше понять природу иррациональных чисел и поспособствовало их признанию.
В современных учебных руководствах основа определения иррационального числа основывается на идееал-Каши, Стевина и Декарта об измерении отрезков и о неограниченном приближении к искомому числу с помощью бесконечных десятичных дробей. Но объяснение свойств действительных чисел и полная теория их были разработаны только в XIX в.
Знак корня (знак радикала) — условное обозначение  для корней, по умолчанию квадратных. В общем случае (для корней n-й степени) показатель степени ставится над «птичкой»: знак
для корней, по умолчанию квадратных. В общем случае (для корней n-й степени) показатель степени ставится над «птичкой»: знак 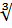 используется для кубических корней,
используется для кубических корней,  — для корней 4-й степени и т. п.; для квадратного корня также можно использовать «полное» обозначение.
— для корней 4-й степени и т. п.; для квадратного корня также можно использовать «полное» обозначение.
Знак корня происходит из строчной латинской буквы r (начальной в лат. radix — корень), сросшейся с надстрочной чертой: в старину надчёркивание выражения использовалось вместо нынешнего заключения его в скобки, так что 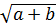 есть всего лишь видоизменённый древний способ записи чего-то вроде
есть всего лишь видоизменённый древний способ записи чего-то вроде 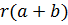 .
.
Впервые такое обозначение использовал немецкий математик Томас Рудольф в 1525 году.
Способы решения иррациональных уравнений
Уравнение– это равенство видаf(  = g(
= g(  , где, чаще всего, в качестве f и g выступают различные функции.
, где, чаще всего, в качестве f и g выступают различные функции.
Можно сформулировать данное определение несколько по-иному:
Уравнением называется математическое соотношение, выражающее равенство двух алгебраических выражений.
Уравнения подразделяются на 2 большие группы: алгебраические и трансцендентные. Алгебраическим называется такое уравнение, в котором для нахождения корня уравнения применяются только лишь алгебраические действия – 4 арифметических, а также возведение в степень и извлечение натурального корня.
Более подробно мы будем рассматривать иррациональные уравнения.
Иррациональным уравнением называют такое уравнение, в котором переменная содержится под знаком радикала или возведенная в дробную степень.
К иррациональным уравнениям относятся уравнения такого вида:
 = B(x),
= B(x),  =
=  , где A(x) и B(x) – выражения с переменной.
, где A(x) и B(x) – выражения с переменной.
Основной идеей решения иррационального уравнения является сведении данного уравнения к рациональному алгебраическому уравнению, которое либо равносильно исходному иррациональному уравнению, либо - его следствие. Главным способом для избавления от корня и получения рационального вида уравнения – это возведение обеих частей данного уравнения в одну и ту же степень, которая имеет корень, включающий неизвестное, и дальнейшее «освобождение» от радикалов по формуле:  =
= 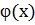
Если обе части иррационального уравнения возвести в одну и ту же нечетную степень и избавиться от радикалов, в таком случае выйдет уравнение, равносильное исходному уравнению. При возведении уравнения в четную степень получают уравнение, являющееся следствием исходного. По этой причине вероятно появление посторонних решений уравнения. Причина приобретения корней заключается в том, что при возведении в четную степень чисел, равных по абсолютной величине, но различных по знаку, получается один и тот же результат. Отметим, что потеря корней при возведении уравнения в четную степень невозможна.
Так как могут появиться посторонние корни, то необходимо делать проверку, подставляя найденные значения неизвестной только в первоначальное уравнение.
Рассмотрим применение данного метода для решения иррациональных уравнений вида: 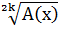 = B(x)
= B(x)
Например, решим иррациональное уравнение:  = 2x+5
= 2x+5
Решение: Нам необходимо сначала возвести обе части в квадрат. Это действие мы производим для того, чтобы избавиться от радикалов.
Благодаря этому, уравнение приобретет привычный нам с Вами вид и решить его нам не составит особых трудностей:
6 – 3x = 4  + 20x + 25
+ 20x + 25
Перенесем все в правую сторону и приравняем к нулю:
4  + 20x + 3x – 6 + 25 = 0
+ 20x + 3x – 6 + 25 = 0
4  + 23x + 19 = 0
+ 23x + 19 = 0
Получили привычное нам квадратное уравнение. Решить его можно с помощью нахождения дискриминанта, либо с помощью теоремы Виета. Воспользуемся дискриминантом:
D = 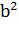 - 4ac = 529 – 4 ⸳ 4⸳ 19 = 529 – 304 = 225;
- 4ac = 529 – 4 ⸳ 4⸳ 19 = 529 – 304 = 225;
 = ±15;
= ±15;
 ;
; 
 = -4,75;
= -4,75;  = -1;
= -1;
Выполним проверку: подставим значение (-4,75) в наше исходное уравнение:
 = -9,5 + 5;
= -9,5 + 5;
 = -4,5 – неверно, соответственно значение (-4,75) не подходит.
= -4,5 – неверно, соответственно значение (-4,75) не подходит.
Подставим значение (-1):
 = -2 + 5
= -2 + 5
3 = 3 – верно, соответственно значение (-1) является корнем данного иррационального уравнения.
Ответ: -1
Для ясности, рассмотрим еще один пример: 
Решение: Для упрощения уравнения возводить обе стороны в квадрат не нужно, достаточно ввести новую переменную, а точнее – сделать замену.

Уравнение становится таким:
y +  = 4
= 4
Умножим все на y и перейдем к квадратному уравнению:
 + 4 = 4y
+ 4 = 4y
 - 4y + 4 = 0
- 4y + 4 = 0
Теорема Виета дала нам одинаковые корни:
 = 2
= 2
Теорема Виета: если 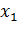 и
и  – корни квадратного уравнения
– корни квадратного уравнения 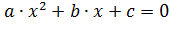 ,то сумма корней равна отношению коэффициентов b и a, взятому с противоположным знаком, а произведение корней равно отношению коэффициентов c и a, то есть,
,то сумма корней равна отношению коэффициентов b и a, взятому с противоположным знаком, а произведение корней равно отношению коэффициентов c и a, то есть,  ,
,  =
= 
Вернемся к нашей замене и найдем решение:
 = 2
= 2
 = 4
= 4
Умножим на x, чтобы могли избавиться от знаменателя:
x + 5 = 4x
x = 
Данный ответ удовлетворяет наше равенство, соответственно ответ 
Рассмотрим уравнение 4x+ 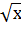 - 5 = 0
- 5 = 0
Решение:
Конечно, можно решить это уравнение методом возведения обеих частей уравнения в одну и ту же степень. Но можно решить и другим способом – методом введения новых переменных.
y = 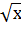
Введем новую переменную. Тогда получим 4y²+y–5=0 – квадратное уравнение относительно переменной y. Найдем его корни:



Так как y= 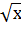 , а
, а  , соответственно,
, соответственно,  не является корнем данного уравнения.
не является корнем данного уравнения.
Ответ: 1
Рассмотрим еще один способ решения иррациональных уравнений.
 +
+ 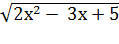 = 3x (1)
= 3x (1)
Решение:
Умножим обе части заданного уравнения на выражение
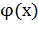 =
=  -
- 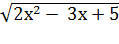 – сопряженное левой части исходного уравнения.
– сопряженное левой части исходного уравнения.
(  +
+ 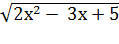 )(
)(  -
- 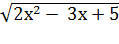 ) =
) =
= (  (
(  ) = 6x
) = 6x
6x = 3x(  -
- 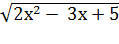 )
)
x(  -
- 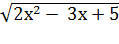 - 2 ) = 0
- 2 ) = 0
Произведение равно нулю тогда и только тогда, когда хотя бы один из множителей равен нулю, а другой при этом известен. Тогда x1=0.Остаётся решить уравнение:
 -
- 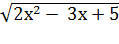 = 2 (2)
= 2 (2)
Сложив уравнения (1) и (2), придём к уравнению:
2  = 3x + 2
= 3x + 2
Решим это уравнение методом возведения в квадрат двух сторон:
8x² + 12x + 20 = 9x² + 12x + 4
-x² + 16 = 0
x² = 16
x = ±4
Проверка:
 +
+ 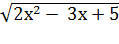 = 3x
= 3x
 ,
,  ,
, 
 +
+  = 3⸳0
= 3⸳0
2 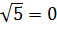 -неверное равенство,значит 1 не является корнем уравнения.
-неверное равенство,значит 1 не является корнем уравнения.
 +
+  = 3⸳4
= 3⸳4
 +
+  = 12
= 12
12 = 12 – верное равенство, соответственно 4 – корень уравнения.
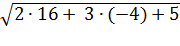 +
+  = 3⸳(-4)
= 3⸳(-4)
 +
+  = -12
= -12
12 = - 12 – неверное равенство, соответственно -4 –не является корнем уравнения.
Ответ: 4
В процессе решения уравнений важно знать, при каких преобразованиях данное уравнение переходит в равносильное ему уравнение.
Теорема 1: Если какое-либо слагаемое перенести из одной части уравнения в другую, изменив его знак, то получим уравнение, равносильное данному.
Доказательство:
Докажем, что уравнение f(x) = g(x)+q(x) (1)
равносильно уравнению
f(x) – q(x) = g(x) (2)
Пусть х=а – корень уравнения. Значит имеет место числовое равенство f(a)=g(a)+q(a) . Но тогда по свойству действительных чисел будет выполняться и числовое равенство f(a)-q(a)=g(a) показывающее, что а – корень уравнения (2). Аналогично доказывается, что каждый корень уравнения (2) является и корнем уравнения (1).
Что и требовалось доказать.
Теорема 2: Если обе части уравнения умножить или разделить на отличное от нуля число, то получим уравнение, равносильное данному.
Доказательство: Обозначим через Т1 - множество решений уравнения (1), а через Т2 - множество решений уравнения (2). Тогда уравнения (1) и (2) будут равносильны, если Т1 = Т2. Чтобы убедиться в этом, необходимо показать, что любой корень из Т1 является корнем уравнения (2) и, наоборот, любой корень из Т2 является корнем уравнения (1).
Пусть число а - корень уравнения (1). Тогда a * Т1, и при подстановке в уравнение (1) обращает его в истинное числовое равенство f(a) = g(a), а выражение h(х) обращает в числовое выражение h(a), имеющее смысл на множестве X. Прибавим к обеим частям истинного равенства f(a) = g(a) числовое выражение h(a). Получим, согласно свойствам истинных числовых равенств, истинное числовое равенство f(a) + h(a) = g(a) + h(a), которое свидетельствует о том, что число а является корнем уравнения (2).
Итак, доказано, что каждый корень уравнения (1) является корнем и уравнения (2), т.е. Т1 с T2.
Пусть теперь а - корень уравнения (2). Тогда а * T2 и при подстановке в уравнение (2) обращает его в истинное числовое равенство f(a) + h(a) = g(a) + h(a). Прибавим к обеим частям этого равенства числовое выражение -h(a), Получим истинное числовое равенство f(х) = g(х), которое свидетельствует о том, что число а - корень уравнения (1).
Итак, доказано, что каждый корень уравнения (2) является и корнем уравнения (1), т.е. T2 с Т1.
Так как Т1 с Т2 и Т2 с Т1, то по определению равных множеств Т1 = Т2, а значит, уравнения (1) и (2) равносильны.
Что и требовалось доказать.
|
из
5.00
|
Обсуждение в статье: Способы решения иррациональных уравнений |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

