 |
Главная |
ПРИМЕРЫ РЕШЕНИЯ ИРРАЦИОНАЛЬНЫХ УРАВНЕНИЙ С ПАРАМЕТРОМ
|
из
5.00
|
Для решения иррациональных уравнений с параметром существует несколько способов. А теперь, давайте разберем некоторые примеры иррациональных уравнений, содержащих параметр:
Пример 1.

Решение:
Перепишем уравнение в следующем виде:
x – 1 -  + 1 – a = 0
+ 1 – a = 0
Рассмотрим его как квадратное относительно  . Находим дискриминант уравнения:
. Находим дискриминант уравнения:
D = 4a – 3
Уравнение (1) имеет решение только в том случае, если a≥ 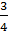 .
.
Имеем: 
Заметим, что уравнение (2) имеет решение тогда и только тогда, когда 1 -  ≥ 0, то есть при a ≤ 1. Решив уравнения (2) и (3), получим при
≥ 0, то есть при a ≤ 1. Решив уравнения (2) и (3), получим при 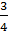 ≤ a ≤ 1:
≤ a ≤ 1:
 ,
, 
Таким образом, приходим к следующему:
при 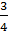 ≤ a ≤ 1 уравнение имеет два корня:
≤ a ≤ 1 уравнение имеет два корня:  ;
;
при а  , уравнение имеет один корень:
, уравнение имеет один корень:  ;
;
приa< 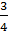 решений нет.
решений нет.
Ответ: при 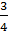 ≤ a ≤ 1 уравнение имеет два корня:
≤ a ≤ 1 уравнение имеет два корня:  ; при а
; при а  , уравнение имеет один корень:
, уравнение имеет один корень:  ; при a<
; при a< 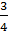 решений нет. [1]
решений нет. [1]
Пример 2.

Решение:
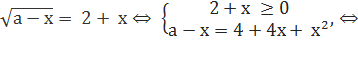
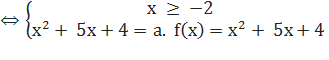
f(x) = a, x ≥ -2
Построим графики этих функций:

Из графика видно, что при x=-2 уравнение имеет единственное решение.
а≥ -2
Ответ: уравнение имеет единственное решение -2.
Пример 3.

Решение:
 + a = x (1)
+ a = x (1)
f(x) = 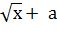
D(f) = 
f(f(x) ) = x⸳ 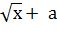 = x
= x
Рассмотрим функцию. Т. к. эта функция возрастает на всей области определения, а уравнение (1) имеет вид, то оно равносильно уравнению:
y = a
Построим графики функций и определим те значения параметра a, при которых функции имеют две общие точки.

y = x - 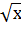
a 
Ответ: уравнение имеет два корня: 0 и 
Пример 4.

Решение:
Рассмотрим графический вариант решения данного уравнения, то есть построим две функции:
 = 2 + x
= 2 + x

Первая функция является линейной и проходит через точки (0; 2) и (-2; 0).
График второй функции содержит параметр. Рассмотрим сначала график этойфункции при а = 0.
При изменении значения параметра график будет передвигаться по оси
ОХ на соответствующее значение влево (при положительных а) или вправо (приотрицательных а).
Из рисунка видно, что при а < -2 графики не пересекают друг друга, а следовательно не имеют общих решений. Если же значение параметра а больше либо равно -2, то графики имеют одну точку пересечения, а следовательно одно решение.

Ответ: при a = -2 уравнение имеет единственное решение.
Пример 4.

Решение:
Построим график функции  .
.
Пусть x ≥ 0, тогдаy =  x² - 2x + 1 – 1 + y² = 0
x² - 2x + 1 – 1 + y² = 0  1 –окружность с центром в точке ( 1; 0 ) и радиусом, равным 1.
1 –окружность с центром в точке ( 1; 0 ) и радиусом, равным 1.
Пусть x< 0, тогда y =  x² + 2x + 1 – 1 + y² = 0
x² + 2x + 1 – 1 + y² = 0  1 –окружность с центром в точке ( -1; 0 ) и радиусом, равным 1.
1 –окружность с центром в точке ( -1; 0 ) и радиусом, равным 1.
y =  ↔
↔ 

Рассмотрим функцию a=y
Это прямая параллельна оси Оx.
Построим следующие случаи этой прямой 1.<1, a <a£1, 0 =1, a >a Из полученного графика хорошо видно, что при )¥+ (1;È;0) ¥-(Îa уравнение решений не имеет, при 1=a уравнение имеет два решения, при 0 – три решения,=a при 1 - четыре решения.< a <0
Ответ: при a  ( -¥; 0)
( -¥; 0)  уравнение решений не имеет; при a = 1 уравнение имеет два решения, при a = 0 – три решения, при 1< a <0 - четыре решения.
уравнение решений не имеет; при a = 1 уравнение имеет два решения, при a = 0 – три решения, при 1< a <0 - четыре решения.
Пример 5.
 =
= 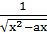
Решение:
D:  , на множестве Dуравнение
, на множестве Dуравнение  +
+  = 1 равносильно исходному.
= 1 равносильно исходному.
Уравнение  +
+  = 1 равносильно системе:
= 1 равносильно системе:

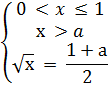

Нам нужно изобразить на плоскости (x, a) график 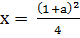 - это парабола с минимумом в точке a = -1, x = 0, пересекающая ось x в точке a = 0, x =
- это парабола с минимумом в точке a = -1, x = 0, пересекающая ось x в точке a = 0, x =  .
.
Укажем также области плоскости (х;а),в которых выполняются неравенства системы:
1. x  - полуплоскость ниже прямой x = a, не включая эту прямую;
- полуплоскость ниже прямой x = a, не включая эту прямую;
2.  - вертикальная полоса между прямыми x = 0 и x=1, включающая правую границу;
- вертикальная полоса между прямыми x = 0 и x=1, включающая правую границу;
3. a ≥ - 1 = полуплоскость выше прямой a = -1, включая эту прямую.
Таким образом, исходное уравнение имеет решение при указанных условиях, иллюстрирующееся частью параболы, заключённой внутри трапеции АВСД, т. е. при a  .
.
При всех остальных действительных значениях a решения нет.

Ответ: 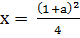 приa
приa  .[1]
.[1]
Пример 6.

Решение:
Положим, что  , где
, где  , так как
, так как  .
.
Тогда, исходное уравнение принимает вид  . Найдем множество значений функции
. Найдем множество значений функции  на отрезке [0;2]. Так как
на отрезке [0;2]. Так как 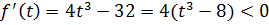 на промежутке [0;2), то функция убывает на отрезке [0;2], и, следовательно, множество ее значений на отрезке [0;2]– отрезок [f(2); f(0)], т.е., отрезок [-48;0]. Таким образом, уравнение
на промежутке [0;2), то функция убывает на отрезке [0;2], и, следовательно, множество ее значений на отрезке [0;2]– отрезок [f(2); f(0)], т.е., отрезок [-48;0]. Таким образом, уравнение  имеет решения тогда и только тогда, когда выполняются условия
имеет решения тогда и только тогда, когда выполняются условия 
 ⇔
⇔  ⇔
⇔  .
.
Ответ:  [13]
[13]
Пример 7.

Решение:
В данной системе вычтем из первого уравнения второе:
 -
- 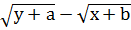 = 0
= 0
 +
+  =
= 
Рассмотрим функцию f(t) =  +
+ 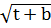
Используя свойство суммы возрастающих функций, делаем вывод, что функция f(t) - возрастающая. Заметим, что f(x) = f(y). Следовательно x = y.
Отсюда получаем
 -
-  = 1
= 1



Очевидно, что  –b ≥ -b
–b ≥ -b
А значит, если a ≥ b + 1, то x = y=  , если a<b + 1, то система не имеет решений.
, если a<b + 1, то система не имеет решений.
А теперь, давайте разберем некоторые примеры иррациональных уравнений, содержащие параметр.
Пример 8.

Произведём замену переменной  , получим:
, получим:
 .
.
Пусть теперь:  ,
,
 .
.
При t ≥ 0 функция g(t) убывает, принимая все значения от g(0) до - 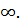 При t < 0 функция g(t) − возрастает, принимая все значения от
При t < 0 функция g(t) − возрастает, принимая все значения от  до g(0). Значит, maxg(t)=g(0)=4
до g(0). Значит, maxg(t)=g(0)=4  .
.
Функция f(t) принимает минимальное значение при  причём на промежутке (0; +∞) — функция возрастает, принимая все значения от
причём на промежутке (0; +∞) — функция возрастает, принимая все значения от  до
до 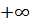 , а на промежутке (−∞; 0) — убывает (функция чётная), принимая все значения от
, а на промежутке (−∞; 0) — убывает (функция чётная), принимая все значения от 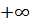 до
до 
Поскольку наибольшее значение функции g(t) и наименьшее значение функции f(t) достигается при одном и том же значенииt=0, уравнение будет иметь решение тогда и только тогда, когда maxg(t) ≥minf(t), то есть
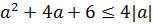
1) При a ≥ 0 получаем

2) При a < 0 получаем

Ответ:  [13]
[13]
Пример 9.

Решение:
Возведем в квадрат:

Неравенство  задает на координатной плоскости «верхнюю» полуплоскость с границей
задает на координатной плоскости «верхнюю» полуплоскость с границей 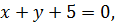 а уравнение
а уравнение  при
при 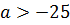 ― окружность с центром P(-5,-5) и радиусом R=
― окружность с центром P(-5,-5) и радиусом R=  (см. рисунок).
(см. рисунок).

Окружность и полуплоскость не имеют общих точек тогда и только тогда, когда радиус окружности меньше половины диагонали PO квадрата APBO, то есть, 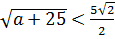 , откуда
, откуда  .
.
При  уравнение, а, следовательно, и вся система решений не имеют, а при
уравнение, а, следовательно, и вся система решений не имеют, а при  решением уравнения является пара (-5;-5), которая не удовлетворяет неравенству
решением уравнения является пара (-5;-5), которая не удовлетворяет неравенству 
Ответ:  [13]
[13]
Пример 10.
При каких значениях параметра а система имеет единственное решение?

Решение:
Эту задачу можно решать аналитически, но оставим ректальные способы решения для любителей. Решим просто.
Посмотрим на второе уравнение системы. Пусть есть точки A(a;0); B(a;3); O(x;y)
Видим, что первый корень – это расстояние между точками А и О, а второй корень – между В и О. Причем нетрудно видеть,что точки А и В лежат на одной и той же вертикальной прямой 
Если хоть немного знать геометрию, становится понятно, что точка О должна лежать на той же прямой между точками А и В. В противном случае сумма расстояний ОА и ОВ будет гарантированно больше 3.
Таким образом, 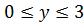 . Первое уравнение можно решить через дискриминант, а можно увидеть по теореме Виета, что
. Первое уравнение можно решить через дискриминант, а можно увидеть по теореме Виета, что  . Условие задачи будет выполнено, если только один из этих корней попадет в отрезок
. Условие задачи будет выполнено, если только один из этих корней попадет в отрезок  .
.
 ⇔
⇔ 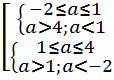 ⇔
⇔ 
Ответ:  [17]
[17]
Пример 11.
Найти наибольшее значение а, при котором неравенство  имеет хотя бы одно решение.
имеет хотя бы одно решение.
Решение:
Для упрощения неравенства сделаем пару замен.

Заметим также, что при  условие задачи выполняется, но это значение а может быть и не наибольшим. Займемся неравенством:
условие задачи выполняется, но это значение а может быть и не наибольшим. Займемся неравенством:


Заметим, что  .
.
Посмотрим теперь насчет множества значений функции 
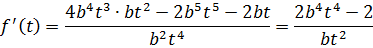
Имеем две точки экстремума 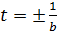 , легко показать, что
, легко показать, что  - точка минимума.
- точка минимума.
 , значит область значений функцииf будет [2b;∞);
, значит область значений функцииf будет [2b;∞);
Для того, чтобы неравенство выполнялось хотя бы для одного t области значений левой и правой частей должны пересекаться:

Таким образом, находим наибольшее значение, о котором спрашивалось в задаче - 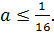
Ответ: 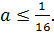 [16]
[16]
Пример 12.
Найдите значения а, при которых уравнение
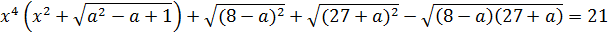
имеет единственное решение.
Решение:
Задачи такого типа обычно имеют достаточно страшное условие, которое крайне тяжело, а то и просто невозможно нормально упростить. Однако, решаются они достаточно просто. Как легко убедиться, функция, получаемая в левой части после перенесения туда 21 будет четной. А четная функция может иметь нечетное число нулей только тогда, когда один из этих нулей будет в точке x = 0.
Уравнение приобретает вид:



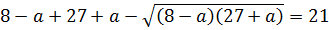

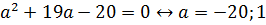
При 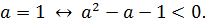
Но нечетное число корней – это не обязательно единственный корень. В нашем уравнении их может быть 3. Поэтому проверим полученны ответ, подставив его в исходное равенство

- единственный действительный корень
Ответ:  [15]
[15]
Пример 13.
При каких значениях параметра b уравнение
 +2
+2 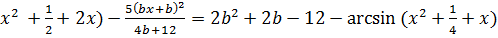
имеет единственное решение?
Решение:
Сделаем замену 
Уравнение приобретает вид:


Видим, что функция в левой части последнего равенства четная. А нечетное число нулей четная функция будет иметь только в том случае, если один из этих нулей при  Подставляем
Подставляем  :
:

Если посмотреть чуть выше, очевидно, что 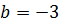 не подходит (деление на 0).
не подходит (деление на 0).
Ответ: 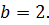 [18]
[18]
Пример 14.
Найдите все значения параметра а, при которых уравнение
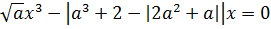
имеет ровно один корень.
Решение:
Как сразу видно, это уравнение всегда имеет корень x=0 независимо от значения параметра. Поэтому уравнение 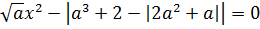 не должно иметь корней. Сначала очевидное – при
не должно иметь корней. Сначала очевидное – при  -корней нет. Значит одно из значений параметра уже есть.
-корней нет. Значит одно из значений параметра уже есть.
Если посмотреть на уравнение  , то видим, что справа стоит неотрицательное выражение. Тогда получается, что всегда будет еще два корня? Но, если еще немного подумать, то видно, что условие задачи будет выполнено, если это уравнение будет иметь единственный и при этом нулевой корень. Тогда:
, то видим, что справа стоит неотрицательное выражение. Тогда получается, что всегда будет еще два корня? Но, если еще немного подумать, то видно, что условие задачи будет выполнено, если это уравнение будет иметь единственный и при этом нулевой корень. Тогда:

При проверке отбросим корни 
Ответ: 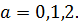 [19]
[19]
Пример 15.
Найдите все значения а, при которых каждое из уравнений
 и
и 
имеет хотя бы один корень.
Посмотрим сначала когда первое уравнение имеет корни. С учетом области значений косинуса выражение под корнем всегда положительное. Получаем:  Поскольку на наличие корней будет влиять знак произведения, стоящего в правой части, можно очень легко выкрутиться из этой ситуации без рассмотрения большого числа случаев. Как всегда, на помощь приходят графики. Рассмотрим функции
Поскольку на наличие корней будет влиять знак произведения, стоящего в правой части, можно очень легко выкрутиться из этой ситуации без рассмотрения большого числа случаев. Как всегда, на помощь приходят графики. Рассмотрим функции  и
и  Точка пересечения этих графиков должна попасть в отрезок [-1;1], поскольку
Точка пересечения этих графиков должна попасть в отрезок [-1;1], поскольку 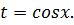

Точка пересечения для возрастающей прямой, для 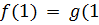 );
);  , для убывающей
, для убывающей  . Не составляет большого труда увидеть, что точка пересечения будет в промежутке от -1 до 1, если
. Не составляет большого труда увидеть, что точка пересечения будет в промежутке от -1 до 1, если 
Теперь займемся вторым уравнением.

Функция, стоящая в правой части достигает своего наименьшего значения -10 в точкеx=-2. График функции в левой части представляет собой «перевернутый» график модуля, смещенный по оси абсцисс на величину а. Для того чтобы уравнение имело корни, должно быть выполнено условие 
Получаем:
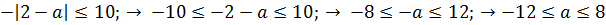
Примечание. Второй случай можно разобрать и иначе, выполнив условие, что наименьшее значение функции  должно быть неположительным. Для этого надо раскрыть модули всеми возможными способами и составить систему неравенств.
должно быть неположительным. Для этого надо раскрыть модули всеми возможными способами и составить систему неравенств.
С учетом условия, полученного для первого уравнения, пишем ответ:
 . [20]
. [20]
Пример 16.
Найдите все значения а, при каждом из которых уравнение
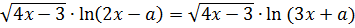
имеет ровно один корень на отрезке [0; 1].
Решение:
Запишем уравнение в виде  и рассмотрим два случая:
и рассмотрим два случая:
Первый случай:  ,при выполнении условий
,при выполнении условий
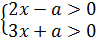 ,
,
то есть если

Второй случай:

Корень  лежит на отрезке [0; 1] при
лежит на отрезке [0; 1] при 
Корни уравнения 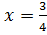 и
и 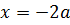 совпадают при
совпадают при 
Таким образом, исходное уравнение имеет ровно один корень на отрезке [0; 1] при 
Ответ: 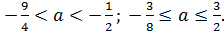 [13]
[13]
ЗАКЛЮЧЕНИЕ
Спецификой уравнений с параметром является то, что наряду с неизвестными величинами в них фигурируют параметры, численные значения которых не указаны конкретно, но считаются известными и заданными на некотором числовом множестве. При этом значения параметров существенно влияют на логический и технический ходырешения задач и на форму ответа.
По данным ФИПИ всего 10% выпускников приступают к решению таких задач, и процент их верного решения невысок: 2–3%, поэтому приобретение навыков решения трудных, нестандартных заданий, в том числе задач с параметрами, учащимися школ по-прежнему остается актуальным.
Решение иррациональных уравнений – наиболее трудный раздел математики. Иррациональные уравнения играют большую роль в формировании логического мышления и математической культуры школьников. Тема актуальна еще тем, что иррациональные уравнения очень часто встречаются на выпускных экзаменах, с их помощью легко диагностируются знания выпускников по многим понятиям, начиная с такого понятия как равносильность уравнений и заканчивая понятием ОДЗ.
Для решения каждого иррационального уравнения необходимо выбирать наиболее удобный способ решения: понятный, доступный, логически и грамотно оформленный.
Таким образом, мы понимаем, что решение иррациональных уравнений требует хороших теоретических знаний, умения применять их на практике, внимания, трудолюбия, сообразительности.
ЛИТЕРАТУРА
1) Кожухова, С.А. Свойства функций в задачах с параметром [Текст]/ С.А. Кожухова, С.К. Кожухов // Математика в школе – 2003. - №7. – С. 17-24.
2) Алгебра [Текст]: учебник для 9 класса средней школы / Ш.А. Алимов [и др.]; отв. ред. А.Н. Тихонов. – М.: Просвещение, 1992.
3) Алгебра [Текст]: учебник для 9 класса средней школы / Ю.Н. Макарычев [и др.]; отв. ред. С.А.
4) Ратников, Н.П. От уравнения с параметром – к графику, задающему параметр [Текст]/ Н.П. Ратников // Математика в школе – 1990. - №3. – С. 80.
5) Открытый урок : [ Электронный ресурс ]., 2003 – 2017. http://xn--i1abbnckbmcl9fb.xn--p1ai/%D1%81%D1%82%D0%B0%D1%82%D1%8C%D0%B8/579138/( Дата обращения на ресурс: 20.04.18).
6) Национальная психологическая энциклопедия: [ Электронный ресурс ]., 2017. https://vocabulary.ru/termin/parametr.html ( Дата обращения на ресурс: 19. 04 .18 ).
7) Электронный научно – практический журнал «Современные научные исследования и инновации» [ Электронный ресурс ]., 2017. http://web.snauka.ru/issues/2015/10/58207 ( Дата обращения на ресурс 20.04.18).
8)Инфоурок [ Электронный ресурс ]., 2017. https://infourok.ru/metody_resheniya_zadach_s_parametrami-398722.htm( Дата обращения на ресурс 21.04.18 )
9) Педагогические технологии и информационное образование [Электронный ресурс].,http://ikted.ru/articles/94/( Дата обращения на ресурс 21.04.2018 )
10) Параметры [ Электронный ресурс ]., http://parametry.narod.ru/uravneniya.html ( Дата обращения на ресурс 21.04.2018 )
11) Дробно – рациональные и иррациональные уравнения и неравенства с параметрами [ Электронный ресурс ]., https://pedportal.net/attachments/000/500/568/500568.pdf?1426921098 ( Дата обращения на ресурс 18.04.2018)
12)Задачи с параметром [ Электронный ресурс]., http://alexlat.ucoz.ru/load/matematika/zadachi_s_parametrami/a_2_x_2ax_2a_3_0/331-1-0-2812 (Дата обращения на ресурс 22.04.2018)
13) Задачи с параметром [Электронный ресурс]., https://ege.sdamgia.ru/test?theme=171 (Дата обращения 22.04.2018)
14) Задачи с параметром [ Электронный ресурс ]., http://alexlarin.net/param/p44.html (Дата обращения 24.04.2018)
15) Решение задач с параметром [ Электронный ресурс ]., http://alexlarin.net/param/p22-23.html (Дата обращения 24.04.2018)
16) Решение задач с параметром[ Электронный ресурс ]., http://alexlarin.net/param/p30.html(Дата обращения 24. 04. 2018)
17) Задачи с параметром [ Электронный ресурс ]., http://alexlarin.net/param/p44.html (Дата обращения 24.04.2018)
18) Задачи с параметром [ Электронный ресурс ]., http://alexlarin.net/param/p29.html (Дата обращения 24.04.2018)
19) Решение задач с параметром [ Электронный ресурс ].,http://alexlarin.net/param/p17.html( Дата обращения 24.04.2018 )
20) Решение задач с параметром [ Электронный ресурс ]., http://alexlarin.net/param/p20.html( Дата обращения 24.04.2018 ).
|
из
5.00
|
Обсуждение в статье: ПРИМЕРЫ РЕШЕНИЯ ИРРАЦИОНАЛЬНЫХ УРАВНЕНИЙ С ПАРАМЕТРОМ |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

