Графический метод. Координатная плоскость (хОс)

Вообще, задачи, содержащие параметр, не обеспечены какой-либо четкой, методически оформленной системой решения. Те или иные значения параметра приходится искать решая большое количество промежуточных задач. Такой подход далеко не всегда обеспечивает успех в отыскании всех значений параметра, при которых задача не имеет решений, имеет одно, два и более решений. Зачастую часть значений параметра теряются или появляются лишние значения. Для того, чтобы находить эти последние значения, приходится проводить специальноеисследование которое может оказаться довольно трудным.

Рассмотрим метод, упрощающий работу по решению задач с параметром. Метод состоит в следующем:

1. Из уравнения (неравенства) с переменной и параметра выразим параметр как функцию от : .

2. В координатной плоскости ( ) строим график функции: .

3. Рассмотрим прямые и выделим те промежутки оси , на которых эти прямые удовлетворяют следующим условиям: a) не пересекает график функции , б) пересекает график функции в одной точке, в) в двух точках, г) в трех точках и так далее.

4. Если поставлена задача найти значения , то выражаем через для каждого из найденных промежутков значения в отдельности.

Взгляд на параметр как на равноправную переменную находит свое отражение в графических методах. Таким образом, возникает координатная плоскость ( ). Казалось бы, такая незначительная деталь, как отказ от традиционного обозначения координатной плоскости буквами и определяет один из эффективнейших методов решения задач с параметрами.

Пример 4:Найдите все значения параметра , при каждом из которых система имеет ровно одно решение.

Изобразим решения системы неравенств на плоскости .(Рисунок 7) Перепишем систему в виде

Первому неравенству удовлетворяют точки, лежащие на параболе и ниже неё, а второму – точки, лежащие на параболе и выше неё. Находим координаты вершин парабол и точек их пересечения, а затем строим график. Вершина первой параболы – второй параболы , точки пересечения – и . Видно, что система имеет ровно одно решение в случаях и

Ответ: Рисунок 7

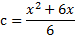
Пример 5: Найдите все значения параметра , при каждом из которых уравнение имеет а) ровно два различных корня; б) ровно три различных корня.

Решение.Изобразим множество решений этого уравнения на плоскости . Оно равносильно совокупности двух уравнений:

1) - это угол с ветвями вверх и вершиной в точке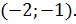

2) - это парабола с ветвями вверх и вершиной в точке (Рисунок 8)

Рисунок 8

Находим точки пересечения двух графиков. Правая ветвь угла задаётся уравнением 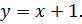Решая уравнение находим, что или . Подходит только значение (т. к. для правой ветви Тогда . Аналогично находим координаты второй точки пересечения -

Возвращаемся к исходной задаче. Уравнение имеет ровно два решения при тех , при которых горизонтальная прямая 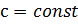пересекает множество решений уравнения в двух точках. По графику видим, что это выполняется при Ровно три решения будут в случае трёх точек пересечения, что возможно только при .

Ответ:а) б)

Пример 6: (решение тремя способами)Для всех действительных значений параметра решите уравнение

Решение.Уравнение равносильно системе:

1 способ (аналитический):Корни квадратного уравнения:

Выясним, при каких значениях они лежат в области решений нет;

Ответ:при решений нет; при

2 способ (графический в плоскости xOy):Преобразуем исходное уравнение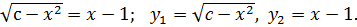

Построим графики функций Решением уравнения будут абсциссы точек пересечения графиков функций. Количество решений - количество точек пересечения (Рисунок 9)

 

 

Рисунок 9

Ответ:при решений нет; при

3 способ (графический в плоскости xOс):Исходное уравнение равносильно системе:

Решение системы - это точки параболы для которых, как видно из рисунка 10, решение существует при , причем каждому значению соответствует одно решение.

 

Рисунок 10

Ответ:при решений нет; при

 

 

Заключение

Подводя итоги можно сделать вывод о том, какой из методов решения наиболее удобный.

Исходя из примеров, приведенных в работе,наглядным способом решения является графический. Этот способ позволяет упростить анализ задач, а в некоторых случаяхявляется единственнымпутем к решению задачи. Также данный метод решения задействует весь набор знаний, связанных с исследованием функции. В то время как аналитический способ решения задач с параметром являетсянаиболее трудным, который требуетбольше знаний высокогоуровня.

Методы решения, приведённые в работе, используются также для всех типов уравнений, неравенств, систем уравнений и неравенств и т.д. Это говорит о том, что база знаний, которая требуются для решения задач с параметром, должна быть изучена в полном объёме, а в процессе решения параметрических уравнений, неравенств и их систем объём знаний будет только увеличиваться и прогрессировать.

Задачи с параметрами являются достаточно сложным типом задач в связи с тем, что нет единого алгоритма их решения. При этом, как уже было отмечено, решение задач такого типаспособствует развитию логического и нестандартного мышления.

Литература

1. Голубев, В. И. Решение сложных и нестандартных задач по математике/ В. И. Голубев-М.: Просвещение, 2007. – 252 с.

2. Денищева, Л. О. Единый Государственный экзамен по математике / Л. О.Денищева, Ю. А. Глазков и др. – М.: Интеллект-Центр, 2009. – 272 с.

3. Козко,А. И. Задачи с параметром и другие сложные задачи/ А. И.Козко, В. Г. Чирский– М.: МЦНМО, 2007. – 296 с.

4. Крамор,В. С. Примеры с параметрами и их решения / В. С. Крамор - М.: АРКТИ, 2001. – 48 с.

5. Крамор, В. С. Задачи с параметрами и методы их решения/ В. С. Крамор – М.: ООО «Издательство Оникс»: ООО «Издательство «Мир и Образование», 2007. – 416 с.

6. Кулабухова,С. Ю. Математика. Подготовка к ЕГЭ-2013 / С. Ю.Кулабухова, Ф. Ф. Лысенко – Ростов-на-Дону: Легион, 2012. – 400 с.

7. Локоть, В. В. Задачи с параметрами / В. В. Локоть– М.: АРКТИ, 2005. – 96 с.

8. Мирошин, В. В. Решение задач с параметрами. Теория и практика/ В. В. Мирошин- М.: Экзамен, 2009. – 286 с.

9. Прокофьев, А. А. Математика. Подготовка к ЕГЭ. Решение задач с параметрами / А.А. Прокофьев, А.Г. Корянов - М.: Легион, 2015. - 336 c.

10. Просветов, Г. И. Задачи с параметрами и методы их решения / Г.И. Просветов - М.: Альфа-пресс, 2010. - 420 c.

11. Рязановский, А.Р. Готовимся к ЕГЭ: Математика - решение задач повышенной сложности / А.Р. Рязановский, В.В. Мирошин- М.: Интеллект-Центр, 2007. - 480 c.

12. Субханкулова, С. А. Задачи с параметрами/ С. А. Субханкулова – М.: ИЛЕКСА, 2010. – 208 с.

13. Шахмейстер, А. Х. Задачи с параметрами на экзаменах / А. Х. Шахмейстер -М.: Издательство МЦНМО: СПб.: «Петроглиф»: «Виктория плюс», 2009. – 248 с.

14. Решение задач с параметром// ЕГЭ по математике URL:http://4ege.ru/matematika/(дата обращения: 15.04.18).

15. Задачи с параметром // ЕГЭ по математике URL: https://academyege.ru/(дата обращения: 17.04.18).

16. Задачи с параметром из ЕГЭ // ЕГЭ по математике URL: https://yourtutor.info/(дата обращения: 19.04.18).