 |
Главная |
Параллельное соединение RLC-элементов
|
из
5.00
|
Для параллельного соединения RLC-элементов (рис. 1) справедливо уравнение первого закона Кирхгофа. Для комплексных токов:

где  - соответственно активная, индуктивная и емкостная проводимости отдельных ветвей цепи.
- соответственно активная, индуктивная и емкостная проводимости отдельных ветвей цепи.

9)Де́льта-фу́нкция (или δ-функция, δ-функция Дирака, дираковская дельта, единичная импульсная функция) — обобщённая функция, которая позволяет записать точечное воздействие, а также пространственную плотность физических величин (масса, заряд, интенсивность источника тепла, сила и т. п.), сосредоточенных или приложенных в одной точке.
Рассмотрим функцию δ (x, γ) колоколообразного типа, зависящую от параметра γ и удовлетворяющую условию
 
| (1) |
при любых (достаточно малых) значениях параметра γ.
Предположим, что при убывании γ график этой функции вытягивается вдоль оси 0y и одновременно сжимается, как это показано на рисунке.


В результате предельного перехода γ → 0 функция δ (x, γ) преобразуется в дельта-функцию Дирака δ (x):
 
| (2) |
При этом
 
| (3) |
В некотором смысле дельта-функция представляет собой обобщение дельта-символа Кронекера, определяемого условиями
 
| (4) |
Очевидно, что дельта-функция является четной функцией,
δ (–x) = δ (x), 
и обладает следующими свойствами:
  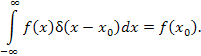 
| (5) |
Действительно, для любого сколь угодно малого числа ε > 0 функция  равна нулю за пределами ε-окрестности точки x0. Поэтому
равна нулю за пределами ε-окрестности точки x0. Поэтому
   
|
Импульсная (весовая) характеристика или импульсная функция  цепи – это ее обобщенная характеристика, являющаяся временной функцией, численно равная реакции цепи на единичное импульсное воздействие на ее входе при нулевых начальных условиях (рис. 13.14); другими словами, это отклик цепи, свободной от начального запаса энергии на дельта-функцию Дирана
цепи – это ее обобщенная характеристика, являющаяся временной функцией, численно равная реакции цепи на единичное импульсное воздействие на ее входе при нулевых начальных условиях (рис. 13.14); другими словами, это отклик цепи, свободной от начального запаса энергии на дельта-функцию Дирана  на ее входе.
на ее входе.

|
10) Метод переменных постоянных
Методом переменных состояния назовем анализ цепи, основанный на решении уравнений состояния (первого порядка), записанных в форме Коши. Таким образом, метод переменных состояния - один из методов расчета прежде всего переходных процессов. Далее предполагается, что цепь имеет только независимые источники и не содержит индуктивных сечений и емкостных контуров. В противном случае составление уравнений становится намного сложнее.
Для линейной цепи с постоянными сосредоточенными параметрами ток каждой ветви, напряжение между выбранными выводами, заряд на обкладках конденсатора и т. д. всегда можно найти как решение составленного для этого тока, напряжения, заряда и т. д. дифференциального уравнения (например, исключением других токов и напряжений из системы уравнений Кирхгофа):

Введением переменных  это уравнение сводится к эквивалентной системе дифференциальных уравнений первого порядка:
это уравнение сводится к эквивалентной системе дифференциальных уравнений первого порядка:

11) Преобразования Лапласа
Преобразование Лапласа - интегральное преобразование, связывающее функцию F(p) комплексного переменного (изображение) с функцией f(x) действительного переменного (оригинал).
Преобразованием Лапласа от функции f(x) (оргигинала) называется функция:

f(x) называют оригиналом преобразования Лапласа, а F(p) - изображением преобразования Лапласа. f(x) и F(p) однозначно определяются друг относительно друга, тоесть если Вы знаете f(x), то всегда можете узнать F(p), и наоборот, если знаете F(p), то всегда можете получить f(x).
Преобразование Лапласа является одним из самых мощных инструментов для решения очень многих задач в области математики, экономики, радиотехники,геометрии, теории управления, микропроцессоров, теории вероятности, теории массового обслуживания и много другого. Часто для решения задачи достаточно получить преобразование Лапласа от искомой функции (именно здесь и пригодится таблица преобразований Лапласа). Также преобразование Лапласа используют при решении задачи Коши для линейного дифференциального уравнения с постоянными коэффициентами, для решения интегральных уравнений, вычисления несобственных интегралов, для представления сигнала в спектральной области и многого другого!
Если в преобразовании Лапласа или таблице преобразований Лапласа Вам что-то не понятно, то Вы всегда можете задать вопрос на нашем форуме, мы будем рады Вам помочь!
Таблица преобразований Лапласа, таблица Лапласа

Теорема подобия. Дополнительное умножение аргумента t в оригинале на число а  R, a > 0 приводит в изображении к уменьшению в а раз параметра p и самого изображения,
R, a > 0 приводит в изображении к уменьшению в а раз параметра p и самого изображения,
f(аt) =:  F(
F(  ). ( 2 )
). ( 2 )
Доказательство.
f(аt) =:  =
= 
 =
= 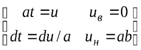 =
=
= 
 =
= 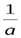
 =
=  F(
F(  )
)
Пр.6 sin at =: 
 =
=  ; cosat =:
; cosat =: 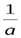
 =
=
Теорема смещения. Переход в изображении от p к (p + z), где z комплексное число, причем Re (p + z) > s0 , приводит к дополнительному умножению оригинала на экспоненту e-zt
F(p + z) =: e-zt f(t) ( 3 )
Доказательство.
e-zt f(t) =:  =
=  = F(p + z)
= F(p + z)
Пр.7 ezt sin at =:  ;ezt cos at =:
;ezt cos at =: 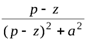
Теорема запаздывания. Уменьшение параметра t в оригинале на величину  > 0 приводит к дополнительному умножению изображения на экспоненту
> 0 приводит к дополнительному умножению изображения на экспоненту 
f(t - 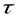 ) =:
) =:  F(p) ( 4 )
F(p) ( 4 )
Доказательство.
f(t - 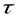 )
) (t-
(t- 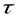 ) =:
) =:  F(p)
F(p)
 (t-
(t- 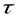 ) - функция Хевисайда (0 если t <
) - функция Хевисайда (0 если t < 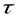 , 1 еслиt<
, 1 еслиt< 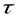 )
)
f(t -  ) =:
) =:  =
=  +
+
+ 
Первый интеграл равен 0, т.к.  (t-
(t- 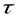 )= 0 при t<
)= 0 при t<  .
.
f(t -  )=:
)=:
 =
=  =
=

 =
= 
 =
=  F(p)
F(p)
Пр.8  (t -
(t -  ) =:
) =:  и (t – a)
и (t – a)  (t - а) =:
(t - а) =:  с учетом Пр. 5 .
с учетом Пр. 5 .
Интеграл свертки
f2(t)=∫0tf1(τ)⋅h(t−τ)dτf2(t)=∫0tf1(τ)⋅h(t−τ)dτ
позволяет при t > 0 найти реакцию f2(t) при произвольном воздействии f1(t) (причем f1 = 0 при t < 0), если известна импульсная характеристика цепи
h(t)=h′1(t)=dh∗1(t)dt⋅δ1(t)+h1(0+)⋅δ(t)=h0(t)+h1(0+)⋅δ(t),h(t)=h′1(t)=dh1*(t)dt⋅δ1(t)+h1(0+)⋅δ(t)=h0(t)+h1(0+)⋅δ(t),
где h1(t) = h1*(t)·δ1(t) – переходная характеристика; δ1(t) – единичная ступенчатая функция; τ – переменная интегрирования; t – текущее время (момент наблюдения). Поскольку t > 0, то все единичные ступенчатые функции под интегралом можно опустить Трудности взятия интеграла свертки возникают, если импульсная характеристика содержит дельта-функцию δ(t). Расчетная формула в этом случае
f2(t)=∫0tf1(τ)⋅h0(t−τ)dτ+h1(0+)⋅f1(t),f2(t)=∫0tf1(τ)⋅h0(t−τ)dτ+h1(0+)⋅f1(t),
где h0(t) — часть импульсной характеристики, не содержащая единичную импульсную функцию.
При использовании операторного метода проще находить реакцию f2(t) по ее изображению
F2(s) = H(s)·Fl(s),
где H(s) – передаточная функция цепи. Интеграл свертки также называют интегралом наложения, выраженным через импульсную характеристику цепи.
12) Законы Кирхгофа и Ома в операторной форме


Связь между током и напряжением. Рассмотрим переход от оригиналов к изображениям в соотношениях, связывающих токи напряжения элементов цепи. Для резистора u = Ri, и в силу линейности преобразования Лапласа такая же связь имеет место и для изображений
 .
.
Связь тока и напряжения на катушке uL = L di/dt перепишем с использованием правила изображения производной
 .
.
Эту же связь можно представить и иначе:
 .
.
Аналогично выполняется переход к изображению связи между током и напряжением конденсатора iC = C duC/dt:

или
 .
.
Из полученных выражений следует, что дифференциальные соотношения для оригиналов заменяются алгебраическими соотношениями для изображений, отражающим все исходные данные задачи, включая начальные условия. В этом и состоит суть операторного метода расчета переходных процессов: дифференциальные уравнения, описывающие переходный процесс, заменяются алгебраическими уравнениями для изображений.
Полученные операторные связи допускают схемную интерпретацию. Выражение для напряжения на катушке позволяет получить схему, приведенную на рис. 19.4, а, в которой эквивалентом катушки является ее операторное сопротивление ZL(s) = sL, включенное последовательно с источником ЭДС EL(s) = LiL(0).

Рис. 19.4
Из выражения, разрешенного относительно тока IL(s), получаем схему с параллельным соединением операторной проводимостикатушки YL(s) = 1/sL и источника тока JL(s) = iL(0)/s (рис. 19.4, б). Аналогичные схемы строятся и для конденсатора. Они включают либо последовательно соединенные операторное сопротивление конденсатора ZC(s) = 1/sC и источник ЭДС EC(s) = uC(0)/s (рис. 19.4, в), либо параллельно соединенные проводимость YC(s) = sC и источник тока JC(s) = CuC(0) (рис. 19.4, г).
|
из
5.00
|
Обсуждение в статье: Параллельное соединение RLC-элементов |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

