 |
Главная |
Графическое изображение расчетной схемы
|
из
5.00
|
В данной части курсовой работы рассмотрен шпангоут с круговой осевой линией нагруженный тремя радиальными силами (  ), двумя касательными силами (
), двумя касательными силами (  ) и двумя изгибающими моментами (
) и двумя изгибающими моментами (  ) (рисунок 2.1). Значения нагрузок приведены в таблице 2.1.
) (рисунок 2.1). Значения нагрузок приведены в таблице 2.1.
|
|
|
|
|
|
|

Рисунок 2.1 – Схема нагружения шпангоута
Таблица 2.1 - Исходные данные
Номер сечения 
| 1 | 2 | 3 | 4 | 5 |
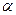 , градусы , градусы
| 25 | 50 | 100 | 220 | 320 |
 , , 
| 25 | -30 | |||
 , , 
| 20 | -35 | 30 | ||
 , , 
| \ | 10 | 7,5 |
Радиус шпангоута 
Расстояние между шпангоутом 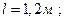
Толщина обшивки 
Коэффициент безопасности 
Материал шпангоута Д16АТ имеет следующие характеристики:

2.2 Определения с помощью ЭВМ закона изменения погонной касательной силы  , изгибающего момента
, изгибающего момента  , перерезывающей силы
, перерезывающей силы  и продольной силы
и продольной силы  . Эпюры
. Эпюры  ,
,  ,
,  и
и 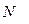
Для расчёта 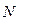 ,
,  и
и  необходимо рассчитать нагрузки с учётом коэффициента безопасности
необходимо рассчитать нагрузки с учётом коэффициента безопасности  . Расчетные значения усилий вычисляются по следующей формуле:
. Расчетные значения усилий вычисляются по следующей формуле:



Где  - расчетные значения усилий;
- расчетные значения усилий;
 - номер нагрузки.
- номер нагрузки.
Для заданного шпангоута имеем:



В соответствии со схемой нагружения шпангоута (Рисунок 2.1) и полученными значениями расчётных нагрузок на ЭВМ вычисляются значения  ,
,  .
.
Расчёт проводится с помощью программы ring.exe. Результаты расчётов приведены в таблице 2.2. Распечатка результатов программы представлена в приложении 3.
Таблица 2.2
| Угол, град | М, кН*м | N, kH | Q, kH | qt, kH/м | Угол, град | М, кН*м | N, kH | Q, kH | qt, kH/м |
| 0 | -2 | 8,735 | 1,59 | -57,25 | 180 | 1,533 | -1,214 | -5,53 | 6,087 |
| 5 | -1,786 | 14,54 | 2,605 | -56,72 | 185 | 0,898 | -12,46 | -6,601 | 9,992 |
| 10 | 1,438 | 20 | 4,1 | -54,4 | 190 | 0,149 | -13,06 | -7,71 | 13,37 |
| 15 | -0,9 | 25,17 | 6,097 | -50,64 | 195 | 0,71 | -13,89 | -8,88 | 16,12 |
| 20 | -0,14 | 29.56 | 8,491 | -45 | 200 | 1,715 | -14,86 | -10,14 | 18,24 |
| 25 | 0,88 | 7,05 | 11,23 | -37,82 | 205 | 2,846 | -15,91 | -11,48 | 19,76 |
| 30 | 2,096 | 9,56 | 11,96 | -29,18 | 210 | 4,123 | -16,98 | -12,92 | 20,79 |
| 35 | 3,39 | 11,03 | 12,87 | -19,42 | 215 | 5,555 | -18 | -14,44 | 21,45 |
| 40 | 4,79 | 11,35 | 13,85 | -8,92 | 220 | 5,849 | 26,56 | -16,06 | 21,84 |
| 45 | 6,296 | 10,47 | 14,81 | 1,857 | 225 | 4,287 | 25,57 | -13,78 | 22,04 |
| 50 | 7,892 | 8,392 | -16,85 | 12,39 | 230 | 2,959 | 24,36 | -11,6 | 22,05 |
| 55 | 6,165 | 8,014 | -16,13 | 22,13 | 235 | 1,854 | 22,98 | -9,53 | 21,86 |
| 60 | 4,511 | 6,62 | -15,48 | 30,57 | 240 | 0,958 | 21,46 | -7,593 | 21,4 |
| 65 | 2,917 | 4,381 | -15 | 37,25 | 245 | 0,258 | 19,84 | -5,79 | 20,61 |
| 70 | 1,362 | 1,517 | -14,74 | 41,83 | 250 | 0,2597 | 18,17 | -4,132 | 19,46 |
| 75 | -0,1795 | -1,719 | -14,75 | 44,12 | 255 | 0,61 | 16,50 | -2,619 | 17,93 |
| 80 | -1,737 | -5,058 | -15,04 | 44,04 | 260 | 0,8132 | 14,89 | -1,25 | 16,03 |
| 85 | -3,34 | -8,231 | -15,62 | 41,7 | 265 | 0,878 | 13,38 | 0,0168 | 13,82 |
| 90 | -5,018 | -10,99 | -16,47 | 37,34 | 270 | 0,8211 | 12 | 1,09 | 11,31 |
| 95 | -6,796 | -13,11 | -17,52 | -31,31 | 275 | 0,654 | 10,83 | 2,085 | 8,567 |
| 100 | -8,693 | -14,44 | 20,27 | 24,10 | 280 | 0,3877 | 9,866 | 2,987 | 5,606 |
| 105 | -6,643 | -18,26 | 18,84 | 16,23 | 285 | 0,031 | 9,145 | 3,814 | 2,46 |
| 110 | -4,758 | -21,11 | 17,11 | 8,250 | 290 | 0,4094 | 8,692 | 4,591 | -0,853 |
| 115 | -3,066 | -22,99 | 15,18 | 0,6744 | 295 | 0,9295 | 8,529 | 5,340 | -4,340 |
| 120 | -1,584 | -23,93 | 13,12 | -6,063 | 300 | 1,528 | 8,676 | 6,088 | -8,022 |
| 125 | -0,319 | -24,05 | 11,03 | -11,63 | 305 | 2,206 | 9,154 | 6,864 | -11,95 |
| 130 | 0,7264 | -23,47 | 8,948 | -15,80 | 310 | 2,967 | 9,989 | 7,697 | -16,17 |
| 135 | 1,558 | -22,36 | 6,945 | -18,45 | 315 | 3,821 | 11,21 | 8,618 | -20,73 |
| 140 | 2,185 | -20,87 | 5,057 | -19,58 | 320 | 4,973 | -26,17 | 9,66 | -25,62 |
| 145 | 2,622 | -19,19 | 3,308 | -19,26 | 325 | 4,078 | -23,96 | 7,472 | -30,79 |
| 150 | 2,883 | -17,47 | 1,709 | -17,62 | 330 | 3,400 | -21,02 | -5,504 | -36,08 |
| 155 | 2,985 | -15,84 | 0,2566 | -14,88 | 335 | 2,915 | -17,37 | 3,823 | -41,31 |
| 160 | 2,942 | -14,43 | -1,062 | -11,30 | 340 | 2,588 | -13,06 | 2,491 | -46,20 |
| 165 | 2,766 | -13,31 | -2,271 | -7,141 | 345 | 2,379 | -8,165 | 1,561 | -50,51 |
| 170 | 2,469 | -12,55 | -3,396 | -2,691 | 350 | 2,245 | -2,799 | 1,079 | -53,94 |
| 175 | 2,057 | -12,16 | -4,472 | 1,795 | 355 | 2,136 | 2,892 | 1,082 | -56,26 |
В таблице 2.2 для сечений 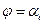 представлены значения внутренних силовых факторов, соответствующие подходы к этим сечениям со стороны углов
представлены значения внутренних силовых факторов, соответствующие подходы к этим сечениям со стороны углов  больших
больших 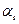 , т.е. даны значения
, т.е. даны значения  (здесь под
(здесь под  понимается любая из величин
понимается любая из величин  и
и  ).
).
1. По таблице 2.2 для сечения  имеем:
имеем:
 .
.
На эпюре  будет скачок на величину
будет скачок на величину 

Что касается нормальной силы  , и изгибающего момента то M они при
, и изгибающего момента то M они при  непрерывны.
непрерывны.
2. Для сечения 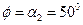 имеем:
имеем:
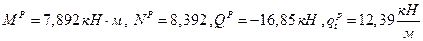 .
.
На эпюре  будет скачок на величину
будет скачок на величину  .
.

Изгибающий момент  и нормальная сила
и нормальная сила  при
при  непрерывны.
непрерывны.
3. Для сечения 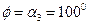 имеем:
имеем:
 .
.
На эпюре 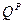 будет скачок на величину
будет скачок на величину  .
.

Изгибающий момент  и нормальная сила
и нормальная сила  при
при 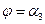 непрерывны.
непрерывны.
4. Для сечения  имеем:
имеем:
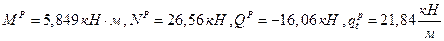 .
.
На эпюре  будет скачок на величину
будет скачок на величину 
На эпюре М будет скачок на величину 
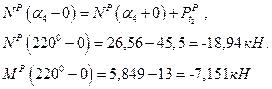
Перерезывающая сила  при
при 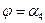 непрерывна.
непрерывна.
5. Для сечения  имеем:
имеем:
 .
.
На эпюре  будет скачок на величину
будет скачок на величину 
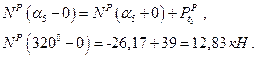
На эпюре  будет скачок на величину
будет скачок на величину 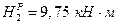 .
.

Нормальная сила  при
при  непрерывна.
непрерывна.
На рисунке 2.2 представлены графики распределения усилий 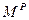 ,
,  ,
, 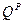 и
и  вдоль осевой линии шпангоута.
вдоль осевой линии шпангоута.

Рисунок 2.2 - Графики распределения усилий 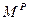 ,
, 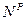 ,
,  и
и 
| |
 ,
, 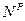 ,
,  и
и  , представлены на рисунках 2.3 – .2.6.
, представлены на рисунках 2.3 – .2.6.

| |
Рисунок 2.3
| |
| |

Рисунок 2.4 - Эпюра 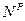

Рисунок 2.5 - Эпюра 

Рисунок 2.6 - Эпюра 
|
из
5.00
|
Обсуждение в статье: Графическое изображение расчетной схемы |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

