Метод Гаусса решения общей системы с линейных уравнений

Практическое значение правила Крамера для решения системы n линейных уравнений с п неизвестными невелико, так как при его применении приходится вычислять п +1 определителей n-го порядка: D , D _{x 1} , D _{x 2} , …, D x_n. Более удобным является так называемый метод Гаусса. Он применим и в более общем случае системы линейных уравнений, т. е. когда число уравнений не совпадает с числом неизвестных.

Итак, пусть дана система, содержащая m линейных уравнений с п неизвестными:

а₁₁х₁ + а₁₂х₂ + …+ а_{1 n} х_n = b₁;

а₂₁х₁ + а₂₂х₂ + …+ а_{2 n} х_n = b₂; (6)

_. ……………………………………

а_m1х₁ + а_m2х₂ + …+ а_{m n} х_n = b_m

Требуется найти все решения системы уравнений (6). Будем производить над системой элементарные преобразования: исключение из системы уравнения вида

0х₁ + 0х₂ + …+ 0х_n = 0(7)

и прибавление к обеим частям одного из уравнений системы соответствующих частей другого уравнения, умноженных на любое число l .

Очевидно, что если мы проделаем над уравнениями системы (6) любое из приведенных выше преобразований, то получим систему, равносильную исходной. При необходимости систему (6) будем подвергать еще одному виду преобразований – перенумерации переменных и уравнений. Идея этого преобразования заключается в следующем. Если, например, возникает необходимость, чтобы в каком-то уравнении системы (например, в k -м) неизвестная x ₁ стояла на первом месте, то в результате перенумерации соответствующее уравнение запишется в виде

a_kix₁ +... + a_k2x₂ + … + a_k1x_i+... + a_knx_n = b_k,

т. е. вместо прежней неизвестной х_i мы будем писать х₁, а вместо x ₁ – х _i Метод Гаусса решения системы (6) заключается в последовательном исключении переменных.

Если среди уравнений системы есть хотя бы одно уравнение вида

0 x_l + 0 x ₂ +... + 0 x_n = b _, (8)

причем b 0, то совершенно очевидно, что ни одна система значений х₁, х₂..., х_п не удовлетворяет этому уравнению, а следовательно, и системе в целом, поэтому система несовместна.

Пусть теперь система (6) не содержит уравнений вида (7) или (8). Это значит, что в каждом уравнении системы хотя бы один из коэффициентов отличен от нуля. Пусть a ₁₁ 0 (в противном случае, применив элементарные преобразования, мы сможем добиться, чтобы первый коэффициент первого уравнения был отличен от нуля). Оставив первое уравнение без изменения, исключим из всех уравнений системы (6),начиная со второго, неизвестную х₁. Для этого из второго уравнения вычтем первое, умноженное на a ₂₁/a ₁₁, затем из третьего уравнения вычтем также первое, но уже умноженное на a ₃₁/a ₁₁, и так до последнего уравнения. В результате этих преобразований мы получим равносильную систему

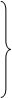 а₁₁х₁ + а₁₂х₂ + … + а_{1 n} х_n = b_1;

а′₂₂х₂ + …+ а′_{2 n} х_n = b′_2;

………………………… (9)

а′_m2х₂ + …+ а′_{m n} х_n = b′_m

Заметим, что в системе (9) число уравнений может быть и меньше m, так как среди них могут оказаться уравнения вида (7), которые, как мы условились ранее, можно отбросить.

Пусть а₂₂ 0. Применим те же самые рассуждения и исключим из последних п – 2 уравнений системы (9) неизвестную х₂ путем вычитания из третьего уравнения второго, умноженного на a ′₃₂/a ′_22, из четвертого уравнения — второго, умноженного на a ′₃₄/a ′₂₂ и т. д. В результате получим систему

а₁₁х₁ + а₁₂х₂ + а₁₃х₃ + …+ а_{1 n} х_n = b_1;

а′₂₂х₂ + а′₂₃х₃ + …+ а′_{2 n} х_n = b′_2;

а′′₃₃х₃ + …+ а″₃х_n = b″_3;

……………………………

а″_m3х₃ +…+а″_{m n} х_n = b″_m

_.

Продолжая этот процесс, систему (6) приведем к равносильной системе вида

c₁₁х₁ + c ₁₂ х₂ + c ₁₃ х₃ + …+ c _{1 k} х _k + …+ c _{1 n} х _n = d _1;

c ₂₂ х₂ + c ₂₃ х₃ + …+ c _{2 k} х _k + …+ c _{2 n} х _n = d _2;

c ₃₃ х₃ + …+ c _{3 k} х _k + …+ c _{3 n} х _n = d _3; (10)

………………………………………

c_kk х _k + …+ c_kn х _n = d_{k .}

в которой коэффициенты c_11, c _22,..., c_kk отличны от нуля.

Может оказаться, что в процессе преобразования на каком-то шаге в полученной системе окажется уравнение вида (8). В этом случае система (7) не имеет решений. Предположим теперь, что среди уравнений полученной системы нет уравнения вида (8). Тогда для решения системы (6) необходимо решить систему (9), что не составляет особого труда. Рассмотрим два возможных случая.

1. k = n (это частный случай, когда число уравнений совпадает с числом неизвестных). Тогда последнее уравнение системы (10) имеет вид с_ппх_п = d_n , откуда х_п = d_n / c_nn . Подставив это значение в предпоследнее уравнение системы (7), имеющее вид

c_{n -1 n -1} x_{n -1} + c_{n -1 n} x_n= d_{n -1} , найдем значение неизвестной x_{n -1} и т. д.; наконец, из первого уравнения найдем неизвестную x ₁ Таким образом, в случае k = п система уравнений (6) имеет единственное решение.

2. k < n . Тогда из последнего уравнения системы (10), найдем неизвестную x_k , выраженную через неизвестные х_k+1, х_k+2,... x_{n :}

x_k = (d_kk – c_{k k +1} x_{k +1} – … – c_knx_n)

Подставив это значение неизвестной в предпоследнее уравнение системы (10), найдем выражение для неизвестной х_k-1,и т. д.; наконец, подставив значения неизвестных х_k, х_k-1,... x ₂ в первое уравнение системы (10), получим выражение для неизвестной x₁. В результате указанная система уравнений (6) приводится к виду

x₁ = d′₁ + c′_{1 k+1}x_k+1 + …+ c′_1nx_n;

x₂ = d′₂ + c′_{2 k+1}x_k+1 + …+ c′_2nx_n; (11)

………………………………………

x_k = d′_k + c′_{k k+1} x_k+1 + …+ c_knx_n.

Неизвестные х_k+1, х_k+2, …, х_п называются свободными. Им можно придать различные значения и затем из системы (6) найти значения неизвестных х_1, х₂, …, х _k . Таким образом, в случае k < п совместная система уравнений (6) имеет бесчисленное множество решений.

Заметим, что если в процессе приведения системы (6) к системе (11) была произведена перенумерация неизвестных, то в системе (11) необходимо вернуться к их первоначальной нумерации.

На практике процесс решения системы уравнений облегчается тем, что указанным выше преобразованиям подвергают не саму систему, а матрицу, составленную из коэффициентов уравнений системы (6) и их свободных членов. При этом каждому элементарному преобразованию, проведенному над системой (6), соответствует преобразование над матрицей (12): вычеркивание строки, все элементы которой состоят из нулей, прибавление к элементам некоторой строки соответствующих элементов другой строки, умноженных на некоторое число, и перестановка двух столбцов матрицы (12).

Пример 1. Решить методом Гаусса систему уравнений

x ₁ – 2 x ₂ + x ₃ + x ₄ = –1;

3 x ₁ + 2 x ₂ – 3 x ₃ – 4 x ₄ = 2;

2 x ₁ – x ₂ + 2 x ₃ – 3 x ₄ = 9;

x ₁ + 3 x ₂ – 3 x ₃ – x ₄ = –1.