 |
Главная |
О произведении 2-разложимой группы и группы Шмидта
|
из
5.00
|
Пусть конечная группа 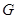 является произведением двух своих подгрупп
является произведением двух своих подгрупп 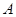 и
и 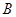 , причем
, причем 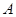 есть группа Шмидта, т. е. ненильпотентная группа, все собственные подгруппы которой нильпотентны. Признаки разрешимости группы
есть группа Шмидта, т. е. ненильпотентная группа, все собственные подгруппы которой нильпотентны. Признаки разрешимости группы  при дополнительных ограничениях на подгруппы
при дополнительных ограничениях на подгруппы 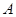 и
и 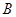 получили Б. Хупперт(2), В. А. Ведерников(4), И. П. Докторов(4), П. И. Трофимов(3). Если
получили Б. Хупперт(2), В. А. Ведерников(4), И. П. Докторов(4), П. И. Трофимов(3). Если 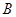 дедекиндова, т. е. в
дедекиндова, т. е. в 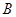 все подгруппы инвариантны, то простая группа
все подгруппы инвариантны, то простая группа 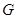 описана автором в(5). Как сообщил недавно С. А. Сыскин, им изучена простая группа
описана автором в(5). Как сообщил недавно С. А. Сыскин, им изучена простая группа 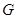 в случае, когда
в случае, когда 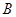 --- нильпотентная группа.
--- нильпотентная группа.
Основным результатом настоящей заметки является
Теорема Пусть 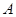 есть группа Шмидта,
есть группа Шмидта, 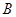 --- 2-разложимая группа, порядки
--- 2-разложимая группа, порядки 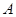 и
и 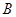 взаимно просты. Если
взаимно просты. Если 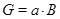 и
и 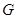 --- конечная неразрешимая группа, то
--- конечная неразрешимая группа, то  ,
,  ,
, 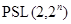 и
и  --- простое число
--- простое число 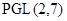 или
или 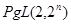 для некоторого простого
для некоторого простого  .
.
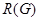 обозначает наибольшую разрешимую инвариантную в
обозначает наибольшую разрешимую инвариантную в  подгруппу.
подгруппу.
Из этой теоремы непосредственно следует описание простых групп  , если
, если 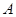 --- группа Шмидта, а
--- группа Шмидта, а 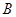 ---
---  -разложимая группа, где
-разложимая группа, где  состоит из простых делителей порядка
состоит из простых делителей порядка 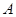 и 2 (см. теорему(2)). В теореме (5) доказано, что неразрешимая группа
и 2 (см. теорему(2)). В теореме (5) доказано, что неразрешимая группа  , где подгруппа
, где подгруппа 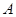 есть группа Шмидта, а
есть группа Шмидта, а 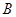 --- нильпотентная подгруппа, есть группа из заключения теоремы(4).
--- нильпотентная подгруппа, есть группа из заключения теоремы(4).
Рассматриваются только конечные группы.  обозначает порядок группы
обозначает порядок группы  , а
, а  --- множество всех простых делителей
--- множество всех простых делителей  . Если
. Если  --- некоторое множество простых чисел, то
--- некоторое множество простых чисел, то  --- наибольшая инвариантная в
--- наибольшая инвариантная в 
 -подгруппа.
-подгруппа.  --- подгруппа, порожденная всеми сопряженными с
--- подгруппа, порожденная всеми сопряженными с  подгруппами в
подгруппами в  . Остальные обозначения можно найти в [??].
. Остальные обозначения можно найти в [??].
Свойства групп Шмидта хорошо известны [??], наиболее полно они изложены в(5). В данной работе они используются без ссылок.
Следующие два результата о простых группах понадобятся при доказательстве.
Теорема Мазуров -- Сыскин 9 Если 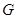 --- простая группа с силовской 2-подгруппой, изоморфной неабелевой силовской 2-подгруппе из группы Шмидта, то
--- простая группа с силовской 2-подгруппой, изоморфной неабелевой силовской 2-подгруппе из группы Шмидта, то  для некоторого
для некоторого  .
.
Теорема Гольдшмидт 10 Если в простой группе 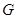 силовская 2-подгруппа
силовская 2-подгруппа  неабелева и
неабелева и  , для всех
, для всех  и некоторой абелевой неединичной подгруппы
и некоторой абелевой неединичной подгруппы  из
из 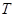 , то
, то  или
или  .
.
Лемма Пусть разрешимая группа  , где
, где  --- группа нечетного порядка,
--- группа нечетного порядка,  --- 2-замкнутая группа четного порядка и
--- 2-замкнутая группа четного порядка и 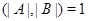 . Если
. Если  , то
, то 
Доказательство проведем индукцией по порядку группы  . Введем следующие обозначения:
. Введем следующие обозначения:  ;
; 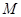 --- минимальная инвариантная в
--- минимальная инвариантная в  подгруппа;
подгруппа; 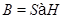 ;
;  --- силовская 2-подгруппа;
--- силовская 2-подгруппа;  --- ее дополнение. Ясно, что
--- ее дополнение. Ясно, что  . Если
. Если  , то
, то  , отсюда и
, отсюда и  . Пусть
. Пусть  и
и  --- минимальная инвариантная
--- минимальная инвариантная  -подгруппа в
-подгруппа в  . Тогда
. Тогда  и
и  , где
, где 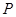 --- силовская
--- силовская 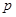 -подгруппа
-подгруппа  для
для  . Можно считать, что
. Можно считать, что  , поэтому
, поэтому  . Кроме того,
. Кроме того, 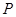 неинвариантна в
неинвариантна в 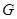 , значит
, значит  --- собственная в
--- собственная в 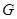 подгруппа. Замечание Фраттини дает, что
подгруппа. Замечание Фраттини дает, что  . Теперь
. Теперь  и
и  . Так как
. Так как  , то
, то  , т. е.
, т. е. 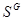 --- собственная в
--- собственная в 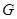 подгруппа. Порядки
подгруппа. Порядки 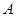 и
и 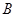 взаимно просты, поэтому
взаимно просты, поэтому  . По индукции
. По индукции  , поэтому и
, поэтому и  . Лемма доказана.
. Лемма доказана.
Доказательство теоремы(4). Допустим, что теорема неверна и группа  --- контрпример минимального порядка. Пусть
--- контрпример минимального порядка. Пусть  ,
, 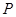 --- инвариантная силовская
--- инвариантная силовская 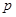 -подгруппа,
-подгруппа,  --- силовская
--- силовская  -подгруппа. Так как факторгруппа группы Шмидта является либо группой Шмидта, либо циклической
-подгруппа. Так как факторгруппа группы Шмидта является либо группой Шмидта, либо циклической  -группой, то благодаря теореме В. А. Ведерникова (5)можно считать, что
-группой, то благодаря теореме В. А. Ведерникова (5)можно считать, что  .
.
Допустим, что группа 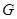 непроста и
непроста и  --- минимальная инвариантная в
--- минимальная инвариантная в  подгруппа. Тогда
подгруппа. Тогда  --- неразрешимая группа.
--- неразрешимая группа.
Предположим, что  не содержит
не содержит 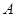 . Тогда
. Тогда 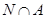 нильпотентна, а так как
нильпотентна, а так как  , то по теореме Я. Г. Берковича (6) подгруппа
, то по теореме Я. Г. Берковича (6) подгруппа 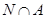 имеет четный порядок. Теперь по теореме 1 из (5) получаем, что силовская 2-подгруппа в
имеет четный порядок. Теперь по теореме 1 из (5) получаем, что силовская 2-подгруппа в  неабелева. Так как
неабелева. Так как  , то из свойств групп Шмидта следует, что
, то из свойств групп Шмидта следует, что 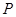 содержится в
содержится в 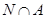 и
и 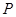 --- силовская 2-подгруппа в
--- силовская 2-подгруппа в 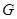 . Если
. Если  непроста, то
непроста, то 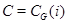 --- неразрешимая группа, где
--- неразрешимая группа, где  --- некоторая инволюция из центра
--- некоторая инволюция из центра 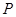 . Так как
. Так как 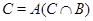 и
и 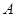 --- группа Шмидта четного порядка, то по индукции
--- группа Шмидта четного порядка, то по индукции  ,
, 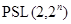 или
или  ,
,  --- простое число. Замечая, что
--- простое число. Замечая, что  и
и 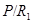 --- абелева группа порядка 4 или
--- абелева группа порядка 4 или  , получаем, что,
, получаем, что,  . Теперь
. Теперь  должно быть четным числом, значит,
должно быть четным числом, значит,  . В этих случаях
. В этих случаях  и
и 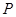 --- группа кватернионов порядка 8, что противоречит тому, что
--- группа кватернионов порядка 8, что противоречит тому, что  . Следовательно,
. Следовательно,  --- простая группа. По теореме Мазурова-Сыскина группа
--- простая группа. По теореме Мазурова-Сыскина группа  изоморфна
изоморфна  . Поэтому
. Поэтому  , значит,
, значит,  и
и

Порядок факторгруппы  равен
равен 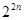 , и
, и  делится на
делится на  . Так как
. Так как  , то
, то  делит порядок
делит порядок 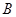 . Это противоречит взаимной простоте порядков факторов.
. Это противоречит взаимной простоте порядков факторов.
Следовательно,  содержит подгруппу
содержит подгруппу 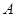 . Так как
. Так как  --- циклическая силовская подгруппа в
--- циклическая силовская подгруппа в  , то
, то  --- простая группа и по индукции
--- простая группа и по индукции  ,
,  или
или  , где
, где  --- простое число. Так как
--- простое число. Так как  ,
,  разрешима, a
разрешима, a  , то
, то  . Теперь
. Теперь 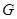 изоморфна некоторой подгруппе из
изоморфна некоторой подгруппе из  . Если
. Если  или
или  , то
, то  или
или  .
.  допускает факторизацию с группой Шмидта порядка 21 и 2-группой порядка 16. Группа
допускает факторизацию с группой Шмидта порядка 21 и 2-группой порядка 16. Группа  не допускает требуемой факторизации. Если
не допускает требуемой факторизации. Если  --- простое число, то и
--- простое число, то и  --- простое число. Так как
--- простое число. Так как  , где
, где  , то
, то  . Противоречие.
. Противоречие.
Таким образом, 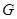 --- простая группа.
--- простая группа.
Предположим, что силовская 2-подгруппа группы  абелева. Тогда по результату Уолтера [??] группа
абелева. Тогда по результату Уолтера [??] группа 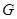 может быть изоморфной только одной из следующих групп:
может быть изоморфной только одной из следующих групп:  ,
,  или
или 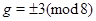 , группе Янко порядка 175560 или группе
, группе Янко порядка 175560 или группе  типа Ри. Из групп
типа Ри. Из групп  для указанных
для указанных  лишь группы
лишь группы  или
или 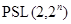 , где
, где  --- простое число, допускают нужную факторизацию [??]. Группа Янко не допускает требуемой факторизации [??]. Порядок группы
--- простое число, допускают нужную факторизацию [??]. Группа Янко не допускает требуемой факторизации [??]. Порядок группы  делится более чем на три простых числа, и силовская 3-подгруппа содержит свой централизатор, элемент порядка 9 и неабелева(5). Поэтому
делится более чем на три простых числа, и силовская 3-подгруппа содержит свой централизатор, элемент порядка 9 и неабелева(5). Поэтому 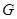 неизоморфна
неизоморфна  .
.
В дальнейшем будем считать, что силовская 2-подгруппа в  неабелева. Так как порядки
неабелева. Так как порядки 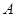 и
и 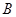 взаимно просты, то некоторая силовская 2-подгруппа
взаимно просты, то некоторая силовская 2-подгруппа  из
из  содержится либо в
содержится либо в 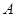 , либо в
, либо в 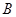 . Если
. Если  , то
, то  и группа
и группа  изоморфна
изоморфна  для некоторого
для некоторого  . Но в этом случае
. Но в этом случае  , поэтому
, поэтому  ,
,  и
и  делит
делит  . Так как
. Так как  , то
, то  делит
делит 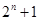 . Но порядок
. Но порядок 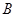 делится на
делится на  , а значит, и на
, а значит, и на  . Противоречие.
. Противоречие.
Следовательно, 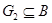 . Теперь
. Теперь  ,
,  ,
,  --- инвариантное 2-дополнение в
--- инвариантное 2-дополнение в 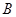 . Если
. Если 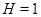 , то
, то  и
и  ввиду леммы Бернсайда [??]. Поэтому
ввиду леммы Бернсайда [??]. Поэтому  ,
, 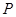 --- элементарная абелева
--- элементарная абелева 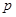 -группа и
-группа и  --- показатель числа
--- показатель числа 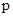 по модулю
по модулю  . Из результатов Уолеса [??] непосредственно получаем, что
. Из результатов Уолеса [??] непосредственно получаем, что  . Противоречие.
. Противоречие.
Значит, 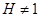 . Введем следующие обозначения:
. Введем следующие обозначения:  --- минимальная инвариантная в
--- минимальная инвариантная в  подгруппа;
подгруппа;  --- силовская подгруппа из
--- силовская подгруппа из  , содержащая
, содержащая  ;
;  ;
;  . Так как
. Так как  , то
, то  и
и  разрешима. Кроме того,
разрешима. Кроме того,  и по лемме С. А. Чунихина ((4), см. также лемму 1.16.1 из(3))
и по лемме С. А. Чунихина ((4), см. также лемму 1.16.1 из(3))  не содержит подгрупп инвариантных в
не содержит подгрупп инвариантных в  . Применяя лемму (??) настоящей работы, получаем, что
. Применяя лемму (??) настоящей работы, получаем, что  . Так как
. Так как  и
и 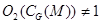 , то и
, то и  . Таким образом,
. Таким образом,  .
.
Пусть  . Покажем, что
. Покажем, что  для всех
для всех  . Возьмем произвольный элемент
. Возьмем произвольный элемент  ,
,  . Тогда
. Тогда  , поэтому
, поэтому  ,
,  . Теперь
. Теперь  . Так как
. Так как  , то
, то 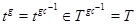 . Применяя результат Гольдшмидта, получаем:
. Применяя результат Гольдшмидта, получаем:  или
или 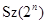 . Но этот изоморфизм ввиду
. Но этот изоморфизм ввиду 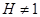 невозможен. Противоречие. Теорема доказана.
невозможен. Противоречие. Теорема доказана.
Лемма Пусть 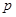 --- простое число, делящее порядки групп
--- простое число, делящее порядки групп 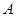 и
и 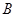 . Если
. Если 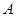 --- группа Шмидта, а
--- группа Шмидта, а 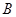 ---
--- 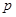 -разложимая группа, то группа
-разложимая группа, то группа  непроста.
непроста.
Доказательство. Пусть  --- силовская
--- силовская 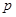 -подгруппа из
-подгруппа из 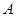 , а
, а 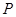 --- силовская
--- силовская 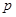 -подгруппа из
-подгруппа из 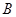 , для которых
, для которых 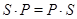 и
и 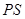 есть силовская
есть силовская 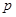 -подгруппа в
-подгруппа в  [??].
[??].
Пусть  инвариантна в
инвариантна в 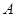 . Тогда для любого
. Тогда для любого 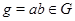 ,
,  ,
,  имеем:
имеем:  . По лемме Кегеля [??] группа
. По лемме Кегеля [??] группа  непроста.
непроста.
Пусть  неинварпантна в
неинварпантна в 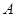 . Тогда
. Тогда  циклическая и каждая собственная подгруппа из
циклическая и каждая собственная подгруппа из  инвариантна в
инвариантна в 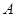 . Если
. Если 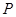 --- силовская подгруппа в
--- силовская подгруппа в  , то
, то  и
и  , где
, где  --- силовская подгруппа из
--- силовская подгруппа из 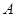 . По лемме Бернсайда группа
. По лемме Бернсайда группа  непроста. Пусть
непроста. Пусть 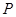 не является силовской в
не является силовской в 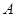 . Тогда
. Тогда 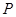 содержится как подгруппа индекса
содержится как подгруппа индекса 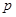 в некоторой группе
в некоторой группе 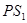 ,
,  . Для элемента
. Для элемента  теперь
теперь 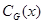 содержит
содержит 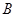 и
и  . Если
. Если 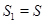 , то
, то 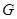 непроста по лемме Бернсайда. Если
непроста по лемме Бернсайда. Если  , то
, то  и
и  непроста по лемме С. А. Чунихина.
непроста по лемме С. А. Чунихина.
Теперь из теоремы (2) и леммы (5) вытекает
Теорема Пусть 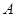 --- группа Шмидта;
--- группа Шмидта; 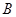 ---
---  -разложимая группа, где
-разложимая группа, где  . Если
. Если  и
и 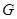 --- простая группа, то
--- простая группа, то  ,
,  или
или 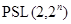 и
и  --- простое число.
--- простое число.
Ясно, что условие теоремы (??) охватывает случай, когда 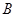 нильпотентна.
нильпотентна.
Теорема Пусть  --- неразрешимая группа, где
--- неразрешимая группа, где 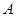 --- группа Шмидта,
--- группа Шмидта, 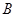 --- нильпотентная группа. Тогда
--- нильпотентная группа. Тогда 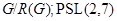 .
.  и
и 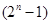 --- простое число,
--- простое число,  или
или  для некоторого простого числа
для некоторого простого числа  .
.
Доказательство. Пусть группа 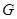 --- контрпример минимального порядка. Как и в теореме (??), пусть
--- контрпример минимального порядка. Как и в теореме (??), пусть  . Ясно, что
. Ясно, что  . Группа
. Группа  не является произведением группы Шмидта и нильпотентной группы, поэтому из теоремы (??) следует, что порядки
не является произведением группы Шмидта и нильпотентной группы, поэтому из теоремы (??) следует, что порядки 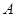 и
и 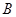 не взаимно просты, а из леммы (??) вытекает, что
не взаимно просты, а из леммы (??) вытекает, что  --- непростая группа.
--- непростая группа.
Допустим, что порядок 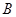 делится на
делится на 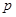 и пусть
и пусть  --- силовская
--- силовская 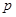 -подгруппа из
-подгруппа из 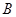 . Тогда
. Тогда  --- неразрешимая группа, поэтому из теоремы Виландта-Кегеля следует, что
--- неразрешимая группа, поэтому из теоремы Виландта-Кегеля следует, что  . Так как
. Так как  есть
есть 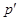 -группа, то
-группа, то 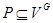 и по лемме из (4) группа
и по лемме из (4) группа  есть
есть 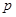 -группа, противоречие. Следовательно, порядок
-группа, противоречие. Следовательно, порядок 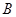 не делится на
не делится на 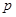 . Но тогда
. Но тогда 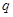 делит порядок
делит порядок 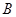 . Рассуждая как и в лемме, получаем, что
. Рассуждая как и в лемме, получаем, что  , а из следует, что
, а из следует, что  .
.
Пусть  --- минимальная инвариантная в
--- минимальная инвариантная в 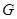 подгруппа. В силу теоремы Виландта-Кегеля
подгруппа. В силу теоремы Виландта-Кегеля  и
и  разрешима. Если
разрешима. Если  , то, применяя к
, то, применяя к 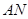 индукцию, получаем, что
индукцию, получаем, что  или
или  и
и  --- простое число, а группа
--- простое число, а группа 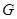 из заключения теоремы, противоречие. Значит,
из заключения теоремы, противоречие. Значит,  , кроме того,
, кроме того,  и
и  , где
, где  --- силовская
--- силовская  -подгруппа из
-подгруппа из  ,
,  --- инвариантное
--- инвариантное 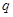 -дополнение в
-дополнение в 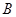 . Проверка показывает, что
. Проверка показывает, что  --- простая группа. Пусть
--- простая группа. Пусть  --- силовская
--- силовская  -подгруппа из
-подгруппа из 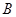 , для которой
, для которой  . Если
. Если  , то централизатор элемента
, то централизатор элемента  из
из  содержит подгруппы
содержит подгруппы  и
и  , что противоречит простоте
, что противоречит простоте 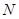 . Далее,
. Далее,  , поэтому
, поэтому  --- подгруппа. Но
--- подгруппа. Но  , значит,
, значит,  .
.
Пусть  --- силовская 2-подгруппа в
--- силовская 2-подгруппа в 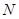 , тогда
, тогда  --- силовская в
--- силовская в  . Как и в теореме (??), можно показать, что
. Как и в теореме (??), можно показать, что  неабелева и
неабелева и 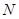 неизоморфна
неизоморфна  . Значит,
. Значит,  . Пусть
. Пусть  ,
,  --- дополнение к
--- дополнение к  в
в  . Если
. Если  , то повторение соответствующих рассуждений из теоремы приводит к противоречию. Значит,
, то повторение соответствующих рассуждений из теоремы приводит к противоречию. Значит, 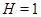 . Так как
. Так как  , то из результата Уолеса заключаем, что
, то из результата Уолеса заключаем, что 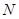 изоморфна одной из следующих групп:
изоморфна одной из следующих групп:  ,
,  ,
,  ,
,  ,
,  ,
, 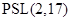 . Для них группа Шмидта
. Для них группа Шмидта 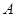 должна иметь соответственно следующие порядки:
должна иметь соответственно следующие порядки:  ,
,  ,
,  ,
,  ,
, 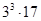 ,
,  , причем
, причем 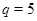 , 5, 7, 7, 13 или 17 соответственно. Но это возможно лишь когда
, 5, 7, 7, 13 или 17 соответственно. Но это возможно лишь когда  или
или  и в
и в 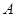 силовская 3-подгруппа
силовская 3-подгруппа 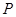 абелева. Так как
абелева. Так как  и в
и в  и
и  силовские 3-подгруппы неабелевы, то получили противоречие. Теорема доказана.
силовские 3-подгруппы неабелевы, то получили противоречие. Теорема доказана.
|
из
5.00
|
Обсуждение в статье: О произведении 2-разложимой группы и группы Шмидта |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

