 |
Главная |
Производящая функция системы функций
|
из
5.00
|
Рассмотрим систему  функций
функций  (с любой общей областью определения), пронумерованных с помощью всех целых чисел:
(с любой общей областью определения), пронумерованных с помощью всех целых чисел:

Составим ряд
 ,
,
где  – комплексная переменная. Предположим, что при каждом
– комплексная переменная. Предположим, что при каждом  (принадлежащем области определения рассматриваемых функций) этот ряд имеет кольцо сходимости, содержащее внутри себя единичную окружность
(принадлежащем области определения рассматриваемых функций) этот ряд имеет кольцо сходимости, содержащее внутри себя единичную окружность  . В частности, это кольцо может представлять собой полную плоскость комплексной переменной без точек 0 и ∞.
. В частности, это кольцо может представлять собой полную плоскость комплексной переменной без точек 0 и ∞.
Функция
 (16)
(16)
(где x лежит в области определения функций системы  ,
,  – внутри кольца сходимости, соответствующего рассматриваемому значению
– внутри кольца сходимости, соответствующего рассматриваемому значению 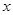 ) называется производящей функцией системы
) называется производящей функцией системы  .
.
Обратно, пусть задана функция 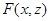 , где
, где 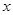 пробегает некоторое множество,
пробегает некоторое множество,  находится внутри некоторого кольца, зависящего от
находится внутри некоторого кольца, зависящего от 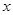 , с центром 0 и содержащего внутри себя единичную окружность. Тогда, если
, с центром 0 и содержащего внутри себя единичную окружность. Тогда, если 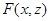 при каждом
при каждом 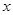 аналитична относительно
аналитична относительно  внутри соответствующего кольца, то
внутри соответствующего кольца, то 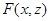 есть производящая функция некоторой системы
есть производящая функция некоторой системы  функций. В самом деле, разложив при каждом
функций. В самом деле, разложив при каждом  функцию
функцию 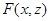 в ряд Лорана по степеням
в ряд Лорана по степеням  :
:
 ,
,
найдем, что система коэффициентов 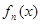 этого ряда будет искомой системой
этого ряда будет искомой системой  .
.
Формулы для коэффициентов ряда Лорана позволяют выразить функции  рассматриваемой системы через производящую функцию. Применяя эти формулы и преобразовывая затем интеграл вдоль единичной окружности
рассматриваемой системы через производящую функцию. Применяя эти формулы и преобразовывая затем интеграл вдоль единичной окружности  в простой интеграл, получим:
в простой интеграл, получим:
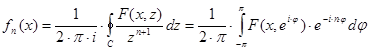 . (17)
. (17)
Производящая функция системы бесселевых функций с целыми индексами
Покажем, что для системы бесселевых функций первого рода с целыми индексами 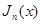 (
(  …) производящая функция есть:
…) производящая функция есть:
 .
.
Имеем:
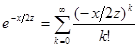 ,
,  ,
,
откуда после почленного перемножения этих равенств найдем:
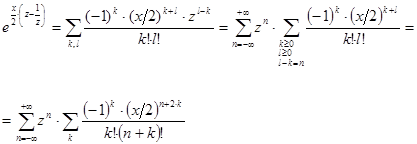
(так как в предпоследней внутренней сумме  и
и  были связаны зависимостью
были связаны зависимостью  , то мы могли положить
, то мы могли положить  , получив суммирование по одному индексу
, получив суммирование по одному индексу  ). В последней внутренней сумме суммирование производится по всем целым
). В последней внутренней сумме суммирование производится по всем целым  , для которых
, для которых  , следовательно, при
, следовательно, при  это будет
это будет 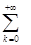 ; при
; при  это будет
это будет  . Таким образом, во всех случаях внутренняя сумма есть
. Таким образом, во всех случаях внутренняя сумма есть 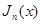 в силу формул (5`) и (5```). Итак,
в силу формул (5`) и (5```). Итак,
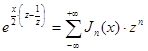 , (18)
, (18)
но это и доказывает, что  есть производящая функция для системы
есть производящая функция для системы  .
.
Выведем некоторые следствия из формулы (18). Полагая в ней  , получим:
, получим:
 ,
,
откуда после разделения действительной и мнимой части (учитывая, что 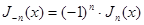 )
)
 (18`)
(18`)
 (18``)
(18``)
Заменяя в (18`) и (18``)  на
на  , найдем:
, найдем:
 , (18```)
, (18```)
 . (18````)
. (18````)
Интегральное представление Jn(x)
Так как, по доказанному, при  имеем
имеем  , то по формуле (17) получаем (используя в преобразованиях формулы Эйлера):
, то по формуле (17) получаем (используя в преобразованиях формулы Эйлера):

где принято во внимание, что  есть четная функция от
есть четная функция от 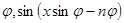 есть нечетная функция от
есть нечетная функция от  . Итак, доказано, что для любого целого числа
. Итак, доказано, что для любого целого числа 
 . (19)
. (19)
Формула (19) дает представление бесселевых функций с целым индексом в виде определенного интеграла, зависящего от параметра  . Эта формула называется интегральным представлением Бесселя для
. Эта формула называется интегральным представлением Бесселя для 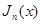 , правая часть формулы называется интегралом Бесселя. В частности, при
, правая часть формулы называется интегралом Бесселя. В частности, при  найдем:
найдем:
 . (19`)
. (19`)
Ряды Фурье-Бесселя
Рассмотрим на каком-либо интервале  (конечном или бесконечном) два дифференциальных уравнения
(конечном или бесконечном) два дифференциальных уравнения
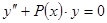 ,
,  , (20)
, (20)
где  и
и  – непрерывные функции на
– непрерывные функции на  . Пусть
. Пусть 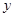 и
и  – ненулевые решения этих уравнений. Умножение на
– ненулевые решения этих уравнений. Умножение на  и на
и на 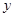 и последующее вычитание дают
и последующее вычитание дают
 .
.
Пусть 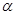 и
и 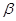 принадлежат
принадлежат  и
и  , тогда после интегрирования в пределах от
, тогда после интегрирования в пределах от 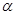 до
до 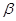 получим
получим
 . (21)
. (21)
Если 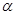 и
и 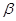 – соседние нули решения
– соседние нули решения  , то между
, то между 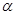 и
и 
 сохраняет постоянный знак, пусть, например,
сохраняет постоянный знак, пусть, например,  на (
на ( 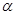 ,
, 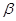 ) (в противном случае следует заменить
) (в противном случае следует заменить 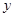 на
на 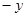 ), тогда
), тогда  ,
,  (равенство нулю исключено, так как
(равенство нулю исключено, так как 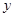 – ненулевое решение дифференциального уравнения второго порядка). Если на
– ненулевое решение дифференциального уравнения второго порядка). Если на 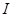
 , то
, то  должна, по крайней мере, раз обращаться в нуль между
должна, по крайней мере, раз обращаться в нуль между  и
и  , так как иначе
, так как иначе  сохранит постоянный знак на (
сохранит постоянный знак на ( 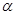 ,
, 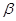 ). Пусть, например,
). Пусть, например,  на (
на (  ,
,  ) (в противном случае заменяем
) (в противном случае заменяем  на
на  ), и тогда из (21) получим противоречие, ибо левая часть ≤0, а правая >0. Таким образом доказана теорема сравнения Штурма: если P(x)<Q(x) на рассматриваемом интервале I и если y и z – ненулевые решения уравнений (20), то между каждыми двумя соседними нулями y(x) находится по крайней мере один нуль z(x).
), и тогда из (21) получим противоречие, ибо левая часть ≤0, а правая >0. Таким образом доказана теорема сравнения Штурма: если P(x)<Q(x) на рассматриваемом интервале I и если y и z – ненулевые решения уравнений (20), то между каждыми двумя соседними нулями y(x) находится по крайней мере один нуль z(x).
Из теоремы сравнения Штурма вытекают нижеследующие следствия. Если 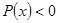 на
на  , то каждое ненулевое решение уравнения
, то каждое ненулевое решение уравнения  может иметь на
может иметь на 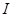 не более одного нуля (это легко видеть, если положить
не более одного нуля (это легко видеть, если положить 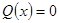 и взять
и взять  ). Если
). Если  на
на  (где
(где  ), то для всяких двух соседних нулей
), то для всяких двух соседних нулей 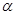 и
и  (
( 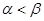 ) каждого ненулевого решения уравнения
) каждого ненулевого решения уравнения 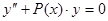 имеем
имеем 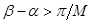 (это легко видеть, если положить
(это легко видеть, если положить  , взять
, взять 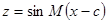 и заметить, что нулями
и заметить, что нулями  будут только числа вида
будут только числа вида  ,
,  целое). Если
целое). Если  на
на  (где
(где  ), то для всяких двух соседних нулей каждого ненулевого решения уравнения
), то для всяких двух соседних нулей каждого ненулевого решения уравнения  имеем
имеем  (это легко видеть, если положить
(это легко видеть, если положить  и взять
и взять  ). Из сказанного следует, что если
). Из сказанного следует, что если  на
на  , то для всяких двух соседних нулей
, то для всяких двух соседних нулей 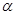 и
и  (
( 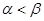 ) каждого ненулевого решения уравнения
) каждого ненулевого решения уравнения 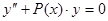 имеем
имеем  .
.
Изложенное показывает, что если 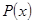 непрерывна на
непрерывна на  и превышает некоторое положительное число вблизи +∞, то каждое ненулевое решение
и превышает некоторое положительное число вблизи +∞, то каждое ненулевое решение  уравнения
уравнения 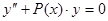 имеет на
имеет на  бесконечно много нулей. Если еще
бесконечно много нулей. Если еще  вблизи
вблизи  не обращается в нуль, то эти нули образуют бесконечную возрастающую последовательность
не обращается в нуль, то эти нули образуют бесконечную возрастающую последовательность  , имеющую пределом +∞, а если, кроме того,
, имеющую пределом +∞, а если, кроме того, 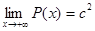 , где
, где 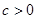 , то
, то 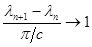 .
.
Рассмотрим уравнение Бесселя

на интервале 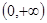 . Подстановка
. Подстановка  приводит к уравнению
приводит к уравнению
 .
.
Очевидно, 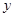 и
и  имеют одни и те же нули. Так как
имеют одни и те же нули. Так как  , где
, где  – целая функция, то
– целая функция, то  не имеет нулей на
не имеет нулей на  при достаточно малом
при достаточно малом  , и так как
, и так как  при
при  , то при каждом
, то при каждом 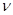 нули
нули  на
на 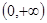 образуют бесконечную возрастающую последовательность
образуют бесконечную возрастающую последовательность

причем  .
.
Если 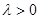 , то
, то  удовлетворит уравнению
удовлетворит уравнению

на интервале (0, +∞). Подстановка  приводит к уравнению
приводит к уравнению

и, следовательно,  удовлетворяет этому уравнению. Таким образом, при любых положительных
удовлетворяет этому уравнению. Таким образом, при любых положительных  и
и  имеем
имеем
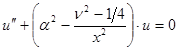 , где
, где  ,
,
 , где
, где  ,
,
откуда
 ,
,
следовательно,
 , где
, где  . (22)
. (22)
Пусть теперь 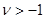 . Разложение
. Разложение  по степеням
по степеням  начинается с члена, содержащего
начинается с члена, содержащего  , разложение
, разложение  по степеням
по степеням  начинается с члена, содержащего
начинается с члена, содержащего  , так как коэффициент при
, так как коэффициент при  равен нулю, что легко видеть, исходя из формулы (5). Следовательно, из (22) при
равен нулю, что легко видеть, исходя из формулы (5). Следовательно, из (22) при 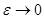 получим
получим
 ,
,
то есть
 , (23)
, (23)
откуда видно, что если 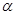 и
и  являются разными нулями функции
являются разными нулями функции  , то
, то
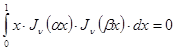 . (23`)
. (23`)
Этим доказано, что при 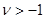 система функций
система функций

на интервале 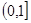 является ортогональной относительно веса
является ортогональной относительно веса  .
.
Переходя к пределу при 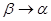 в соотношении
в соотношении

и используя правило Лопиталя, получим при всяком 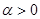
 , (24)
, (24)
следовательно, если 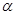 является нулем функции
является нулем функции  , то
, то
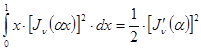 . (24`)
. (24`)
Таким образом, при каждом 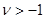 всякой непрерывной функции
всякой непрерывной функции  на
на 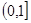 , удовлетворяющей требованию
, удовлетворяющей требованию
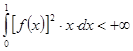 ,
,
поставлен в соответствие ряд Фурье-Бесселя
 , (25)
, (25)
коэффициенты которого определяются формулами
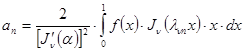 . (25`)
. (25`)
Можно доказать, что система функций  на
на  , ортогональная относительно веса
, ортогональная относительно веса  , замкнутая. В частности, если ряд Фурье-Бесселя (25) равномерно сходится к порождающей его непрерывной функции
, замкнутая. В частности, если ряд Фурье-Бесселя (25) равномерно сходится к порождающей его непрерывной функции  .
.
Можно показать, что если  и
и  непрерывная на
непрерывная на  и кусочно-гладкая на
и кусочно-гладкая на  функция, то ряд Фурье-Бесселя этой функции сходится к ней при
функция, то ряд Фурье-Бесселя этой функции сходится к ней при  .
.
|
из
5.00
|
Обсуждение в статье: Производящая функция системы функций |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

