 |
Главная |
Уравнение колебаний струны.
|
из
5.00
|
ДИПЛОМНАЯ РАБОТА
Использование дифференциальных уравнений в частных производных для моделирования реальных процессов.
|
дневной формы обучения
Специальность 010100
„Математика”
Прокофьевой Я. К.
Студенческий билет № 95035
|
техн. наук
Позин П.А.
Сочи, 2000 г.
СОДЕРЖАНИЕ
Введение………………………………………………………………………..……3
Глава 1. Уравнения гиперболического типа.
§1.1. Задачи, приводящие к уравнениям гиперболического типа..………………5
1.1.1. Уравнение колебаний струны..…………………………………………5
1.1.2. Уравнение электрических колебаний в проводах…….………………8
§1.2. Метод разделения переменных ……………………………………………..10
1.2.1. Уравнение свободных колебаний струны….…………………………10
Глава 2. Уравнения параболического типа.
§2.1. Задачи, приводящие к уравнениям параболического типа………………..17
2.1.1. Уравнение распространения тепла в стержне.……………………….17
2.1.2. Распространение тепла в пространстве.………………………………19
§2.2. Температурные волны.……………………………………………………….23
Глава 3. Моделирование с помощью дифференциальных уравнений в частных производных.
§3.1. Дифракция излучения на сферической частице……………………………29
Заключение………………………………………………………………………….40
Литература…………………………………………………………………………..41
ВВЕДЕНИЕ
Изучением дифференциальных уравнений в частных производных занимается математическая физика. Основы теории этих уравнений впервые были изложены в знаменитом «Интегральном исчислении» Л. Эйлера.
Классические уравнения математической физики являются линейными. Особенность линейных уравнений состоит в том, что если U и V – два решения, то функция aU + bV при любых постоянных a и b снова является решением. Это обстоятельство позволяет построить общее решение линейного дифференциального уравнения из фиксированного набора его элементарных решений и упрощает теорию этих уравнений.
Современная общая теория дифференциальных уравнений занимается главным образом линейными уравнениями и специальными классами нелинейных уравнений. Основным методом решения нелинейных дифференциальных уравнений в частных производных выступает численное интегрирование.
Круг вопросов математической физики тесно связан с изучением различных физических процессов. Сюда относятся явления, изучаемые в гидродинамике, теории упругости, электродинамике и т.д. Возникающие при этом математические задачи содержат много общих элементов и составляют предмет математической физики.
Постановка задач математической физики, будучи тесно связанной с изучением физических проблем, имеет свои специфические черты. Так, например, начальная и конечная стадии процесса носят качественно различный характер и требуют применения различных математических методов.
Круг вопросов, относящихся к математической физике, чрезвычайно широк. В данной работе рассматриваются задачи математической физики, приводящие к уравнениям с частными производными.
Расположение материала соответствует основным типам уравнений. Изучение каждого типа уравнений начинается с простейших физических задач, приводящих к уравнениям рассматриваемого типа.
Глава 1. УРАВНЕНИЯ ГИПЕРБОЛИЧЕСКОГО ТИПА
Задачи, приводящие к уравнениям гиперболического типа.
Уравнения с частными производными 2-го порядка гиперболического типа наиболее часто встречаются в физических задачах, связанных с процессами колебаний. Простейшее уравнение гиперболического типа
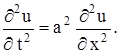
называется волновым уравнением. К исследованию этого уравнения приводит рассмотрение процессов поперечных колебаний струны, продольных колебаний стержня, электрических колебаний в проводе, крутильных колебаний вала, колебаний газа и т.д.
Уравнение колебаний струны.
В математической физике под струной понимают гибкую, упругую нить. Напряжения, возникающие в струне в любой момент времени, направлены по касательной к ее профилю. Пусть струна длины 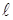 в начальный момент направлена по отрезку оси Оx от 0 до
в начальный момент направлена по отрезку оси Оx от 0 до 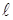 . Предположим, что концы струны закреплены в точках
. Предположим, что концы струны закреплены в точках 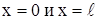 . Если струну отклонить от ее первоначального положения, а потом предоставить самой себе или, не отклоняя струны, придать в начальный момент ее точкам некоторую скорость, или отклонить струну и придать ее точкам некоторую скорость, то точки струны будут совершать движения – говорят, что струна начнет колебаться. Задача заключается в определении формы струны в любой момент времени и определении закона движения каждой точки струны в зависимости от времени.
. Если струну отклонить от ее первоначального положения, а потом предоставить самой себе или, не отклоняя струны, придать в начальный момент ее точкам некоторую скорость, или отклонить струну и придать ее точкам некоторую скорость, то точки струны будут совершать движения – говорят, что струна начнет колебаться. Задача заключается в определении формы струны в любой момент времени и определении закона движения каждой точки струны в зависимости от времени.
Будем рассматривать малые отклонения точек струны от начального положения. В силу этого можно предполагать, что движение точек струны происходит перпендикулярно оси Ox и в одной плоскости. При этом предположении процесс колебания струны описывается одной функцией 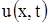 , которая дает величину перемещения точки струны с абсциссой x в момент t.
, которая дает величину перемещения точки струны с абсциссой x в момент t.
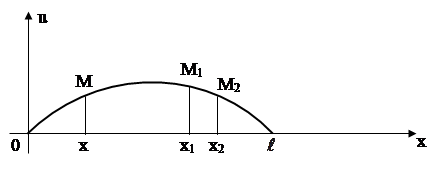 |
Рис. 1.1.
Так как мы рассматриваем малые отклонения струны в плоскости 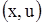 , то будем предполагать, что длина элемента струны
, то будем предполагать, что длина элемента струны  равняется ее проекции на ось Ox, т.е.
равняется ее проекции на ось Ox, т.е. 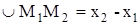 .1 Также будем предполагать, что натяжение во всех точках струны одинаковое; обозначим его через Т.
.1 Также будем предполагать, что натяжение во всех точках струны одинаковое; обозначим его через Т.
Рассмотрим элемент струны 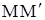 .
.
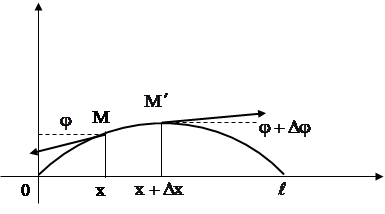 | |||
| |||
Рис. 1.2.
На концах этого элемента, по касательным к струне, действуют силы Т. Пусть касательные образуют с осью Ox углы 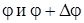 . Тогда проекция на ось Ou сил, действующих на элемент
. Тогда проекция на ось Ou сил, действующих на элемент 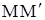 , будет равна
, будет равна 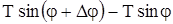 . Так как угол
. Так как угол 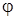 мал, то можно положить
мал, то можно положить 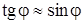 , и мы будем иметь:
, и мы будем иметь:
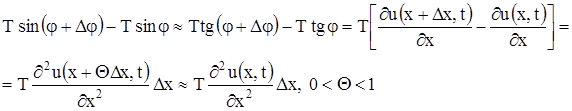
(здесь мы применили теорему Лагранжа к выражению, стоящему в квадратных скобках).
Чтобы получить уравнение движения, нужно внешние силы, приложенные к элементу, приравнять силе инерции. Пусть 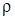 - линейная плотность струны. Тогда масса элемента струны будет
- линейная плотность струны. Тогда масса элемента струны будет 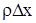 . Ускорение элемента равно
. Ускорение элемента равно 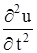 . Следовательно, по принципу Даламбера будем иметь:
. Следовательно, по принципу Даламбера будем иметь:
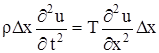 .
.
Сокращая на 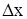 и обозначая
и обозначая 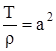 , получаем уравнение движения
, получаем уравнение движения
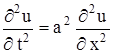 . (1)
. (1)
Это и есть волновое уравнение – уравнение колебаний струны. Для полного определения движения струны одного уравнения (1) недостаточно. Искомая функция 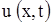 должна удовлетворять еще граничным условиям, указывающим, что делается на концах струны
должна удовлетворять еще граничным условиям, указывающим, что делается на концах струны 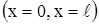 , и начальным условиям, описывающим состояние струны в начальный момент (t = 0). Совокупность граничных и начальных условий называется краевыми условиями.
, и начальным условиям, описывающим состояние струны в начальный момент (t = 0). Совокупность граничных и начальных условий называется краевыми условиями.
Пусть, например, как мы предполагали, концы струны при 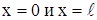 неподвижны. Тогда при любом t должны выполнятся равенства:
неподвижны. Тогда при любом t должны выполнятся равенства:
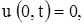 (2’)
(2’)
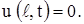 (2’’)
(2’’)
Эти равенства являются граничными условиями для нашей задачи.
В начальный момент t = 0 струна имеет определенную форму, которую мы ей придали. Пусть эта форма определяется функцией f (x). Таким образом, должно быть
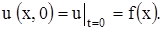 (3’)
(3’)
Далее, в начальный момент должна быть задана скорость в каждой точке струны, которая определяется функцией 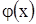 . Таким образом, должно быть
. Таким образом, должно быть
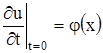 (3’’)
(3’’)
Условия (3’) и (3’’) являются начальными условиями.
Замечание. В частности, может быть 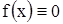 или
или 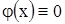 . Если же
. Если же 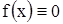 и
и 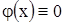 , то струна будет находится в покое, следовательно,
, то струна будет находится в покое, следовательно, 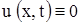 .
.
|
из
5.00
|
Обсуждение в статье: Уравнение колебаний струны. |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

