Понятие сингулярного интеграла

Федеральное агентство по образованию

Государственное муниципальное образовательное учреждение

Высшего профессионального образования

Вятский государственный гуманитарный университет

(ВятГГУ)

Математический факультет

Кафедра математического анализа и методики преподавания математики

Выпускная квалификационная работа

Сингулярные интегралы.

Выполнила:

студентка V курса

математического факультета

Сколова Ирина Юрьевна

____________________

Научный руководитель:

старший преподаватель кафедры математического анализа и МПМ

Гукасов Артур Константинович

____________________

Рецензент:

кандидат физико-математических наук, доцент

Подгорная Ирина Иссаковна

____________________

Допущена к защите в ГАК

Зав. кафедрой     ___________________ Крутихина М. В.

« » _______________

Декан факультета ___________________ Варанкина В. И.

« » _______________

Киров 2005

Оглавление

Введение………………………………………………………………………...с. 3

§1. Понятие сингулярного интеграла…………………………………………с. 6

§2. Представление функции сингулярным интегралом в заданной точке…с. 11

§3. Приложения в теории рядов Фурье.............................................................с. 18

§4. Сингулярный интеграл Пуассона................................................................с. 23

Литература……………………………………………………………………...с. 27

 

 

Введение

Цель работы – познакомиться с понятием сингулярного интеграла, рассмотреть представление функции сингулярным интегралом в заданной точке и приложения в теории рядов Фурье. 

Основной вопрос теории сингулярных интегралов состоит в установлении связи предельных значений интеграла  при  со значением функции f (t) в точке x. Важным также является вопрос о представлении суммируемой функции сингулярным интегралом в точках, где эта функция служит производной своего неопределенного интеграла, или в точках Лебега. Теория сингулярных интегралов имеет многочисленные приложения. Например, вопрос о сходимости ряда Фурье разрешается с помощью сингулярного интеграла.

Во всем дальнейшем интеграл будем понимать в смысле интеграла Лебега. Напомним, что функция называется суммируемой, если существует конечный интеграл от этой функции.

В работе нам будут необходимы следующие определения и теоремы.   

Определение.Если в точке x будет  и , то точка x называется точкой Лебега функции f (t).

Теорема (Н. Н. Лузин). Пусть f (x) измеримая и почти везде конечная функция, заданная на [a, b]. Каково бы ни было δ>0, существует такая непрерывная функция 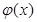, что .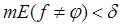

Если, в частности, , то и .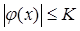

Теорему Н. Н. Лузина можно сформулировать и так: измеримая и почти везде конечная функция становится непрерывной, если пренебречь множеством сколь угодно малой меры.  

Определение. Пусть дано измеримое множество E. Взяв произвольную точку x и число h>0, положим E( , h)=E∙[ -h, +h]. Это тоже измеримое множество.

Предел отношения  при h→0 называется плотностью множества E в точке  и обозначается через .

Определение. Пусть функция f (x) задана на сегменте [a, b] и . Если существует такое измеримое множество E, лежащее на [a, b] и имеющее точку  точкой плотности, что f (x) вдоль E непрерывна в точке , то говорят, что f (x) аппроксимативно непрерывна в точке .     

Определение. Измеримая функция f (x) называется функцией с суммируемым квадратом, или функцией, суммируемой с квадратом, если

                       .

Множество всех функций с суммируемым квадратом обозначается символом .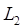

Определение. Пусть на сегменте [a, b] задана конечная функция f (x). Если всякому ε>0 отвечает такое δ>0, что для любой конечной системы взаимно не пересекающихся интервалов 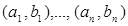, для которой  оказывается

,                                             (3)

то говорят, что функция f (x) абсолютно непрерывна.

Не изменяя смысла определения, можно условие (3) заменить более тяжелым условием .

Определение. Две функции f (x) и g(x), заданные на сегменте [a, b], называются взаимно ортогональными, если .

Определение. Функция f (x), заданная на [a, b], называется нормальной, если .

Определение. Система функций , , , 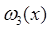…, заданных на сегменте [a, b], называется ортонормальной системой, если каждая функция системы нормирована, а любые две функции системы взаимно ортогональны.

Определение. Пусть 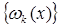 есть ортонормальная система и f (x) некоторая функция из . Числа  называются коэффициентами Фурье функции f (x) в системе .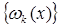

Ряд  называется рядом Фурье функции f (x) в системе .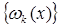

Понятие сингулярного интеграла

Чтобы познакомиться с идеей, лежащей в основе понятия сингулярного интеграла, начнем с примера.

Рассмотрим функцию

                  .                                       (1) 

Если n и x фиксированы, а t меняется от 0 до 1, то эта функция есть непрерывная функция от t. Значит, для всякой суммируемой f (t) ( ) можно образовать величину

                  .                                        (2)

    Докажем, что во всякой точке x (0<x<1), в которой функция f ( t ) непрерывна, будет

                                     .                                          (3)

    Для этого прежде всего отметим, что при

.            (4)

    Поэтому, чтобы установить (3), достаточно показать, что при  стремится к нулю разность

    .

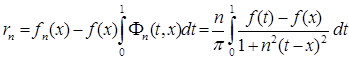    Возьмем произвольное  и найдем такое , что при  будет . Считая, что , представим  в форме

.

Интеграл 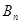 оценивается следующим образом:

.

    В интеграле  будет , поэтому

,

где  не зависит от n. Аналогично 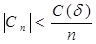 и, следовательно,                                       ,

так что при достаточно больших n будет , т. е.  стремится к 0 с возрастанием n, что и требовалось доказать.

    Соотношение (3) обеспечивают следующие свойства функции : при больших значениях n те значения , которые отвечают сколько-нибудь заметно удаленным от x значениям t, очень малы, так что величина интеграла (2) определяется в основном значениями подынтегральной функции в непосредственной близости точки x. Но около точки x функция f (t) почти равна f (x) (т. к. она непрерывна при t = x). Значит, если n велико, то интеграл (2) мало изменяется при замене f (t) на f (x), т. е. он почти равен интегралу

                 

и, в силу (4), почти равен f (x).

    Функция , обладающая подобными свойствами, носит название ядра.

    Определение.Пусть функция  (n=1, 2, …), заданная в квадрате ( , 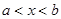), суммируема по t при каждом фиксированном x . Она называется ядром, если  при условии, что .

        

Определение. Интеграл вида , где  есть ядро, называется сингулярным интегралом.

    В теории сингулярных интегралов очень важен вопрос установления связи предельных значений интеграла  при 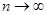 со значением функции

f (t) в точке x. Так как изменение значения функции f (t) в одной точке никак не отражается на величине , то необходимо потребовать, чтобы значение f (x ) функции f (t) в точке x было как-то связано с ее значениями в близких точках. Простейшая форма такой связи есть непрерывность функции f (t) в точке t = x. Другими формами связи могут служить аппроксимативная непрерывность, требование, чтобы x была точкой Лебега функции f (t), и т. п.

    Теорема 1 (А. Лебег). Пусть на [ a , b ] задана последовательность измеримых функций , , , … Если существует такая постоянная K , что при всех n и t будет

                      ,                                                       (5)

и если при всяком c ( 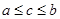) будет

                                 ,                                       (6)

то, какова бы ни была суммируемая на [ a , b ] функция f (t), справедливо равенство

                      .                                 (7)

Доказательство. Если  есть сегмент, содержащийся в [ a , b ], то из (6) следует, что

                                 .                                             (8)

    Рассмотрим непрерывную функцию f (t), и для наперед заданного  разложим [ a , b ] точками  на столь малые части, чтобы в каждой из них колебание f (t)было меньше, чем ε.

Тогда .   (9)

Но 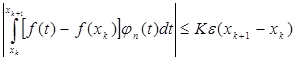, так что первая сумма из (9) не больше, чем Kε ( b - a ). Вторая же сумма (9), в силу (8), стремится к нулю с возрастанием n и для  окажется меньшей, чем ε. Для этих n будет

              ,

так что (7) доказано для непрерывной функции f ( t ).

    Пусть f (t)измеримая ограниченная функция .

    Возьмем ε>0 и, пользуясь теоремой Н. Н. Лузина, найдем такую непрерывную функцию g(t), что , .

    Тогда .

    Но .

Интеграл 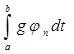 по уже доказанному стремится к нулю и для достаточно больших n становится меньше ε. Значит, для этих n будет

                                 ,

что доказывает (7) для случая ограниченной измеримой функции.

Пусть f (t) произвольная суммируемая функция.

Возьмем ε>0 и, пользуясь абсолютной непрерывностью интеграла, найдем такое δ>0, чтобы для любого измеримого множества  с мерой me<δ было .

    Сделав это, найдем такую измеримую ограниченную функцию g(t), чтобы было . Это возможно по

Теореме. Пусть на множестве Е задана измеримая, почти везде конечная функция f (x). Каково бы ни было ε>0, существует измеримая ограниченная функция g(x) такая, что .

Можно считать, что на множестве  функция g(t) равна нулю.

Тогда .

    Но .

Интеграл же  при достаточно больших n будет меньше ε, и при этих n окажется 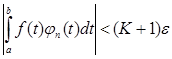, что и доказывает теорему.

Пример. Пусть . Тогда  и . Следовательно выполнены оба условия теоремы Лебега. Аналогично рассматривается случай . Таким образом доказана

    Теорема 2 (Риман-Лебег). Для любой суммируемой на [ a , b ] функции

f (t) будет .

В частности, коэффициенты Фурье ,  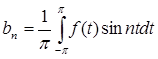произвольной суммируемой функции стремятся к нулю при .

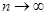    Если соотношение (7) имеет место для всякой суммируемой на [ a , b ] функции f (t), то мы будем говорить, что последовательность  слабо сходится к нулю.