 |
Главная |
Представление функции сингулярным интегралом в заданной точке
|
из
5.00
|
Во всем дальнейшем будем считать, что ядро 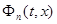 при фиксированных n и x ограничено. Тогда сингулярный интеграл
при фиксированных n и x ограничено. Тогда сингулярный интеграл 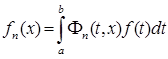 имеет смысл при любой суммируемой функции f (t).
имеет смысл при любой суммируемой функции f (t).
Теорема 1 (А. Лебег). Если при фиксированном x ( a < x < b ) и любом δ>0 ядро 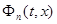 слабо сходится к нулю в каждом из промежутков [ a , x - δ ],
слабо сходится к нулю в каждом из промежутков [ a , x - δ ],
[ x + δ , b ] и 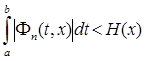 , где H(x) не зависит от n , то, какова бы ни была суммируемая функция f (t), непрерывная в точке x , справедливо равенство
, где H(x) не зависит от n , то, какова бы ни была суммируемая функция f (t), непрерывная в точке x , справедливо равенство
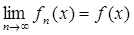 .
.
Доказательство. Так как 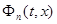 есть ядро, то
есть ядро, то 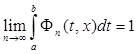 ,
,
и достаточно обнаружить, что
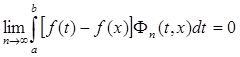 .
.
С этой целью, взяв ε>0, найдем такое δ>0, что при 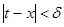 будет
будет
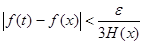 .
.
Это возможно в силу непрерывности функции f в точке x.
Тогда при любом n  .
.
Но каждый из интегралов 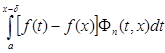 ,
, 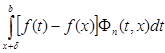 при
при 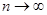 стремится к нулю, т. к.
стремится к нулю, т. к. 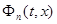 слабо сходится к нулю в каждом из промежутков [ a , x - δ ], [ x + δ , b ]. Поэтому для
слабо сходится к нулю в каждом из промежутков [ a , x - δ ], [ x + δ , b ]. Поэтому для 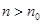 каждый из них будет по абсолютной величине меньше ε/3.
каждый из них будет по абсолютной величине меньше ε/3.
И для этих n окажется 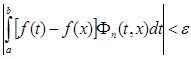 , что и требовалось доказать.
, что и требовалось доказать.
Эта теорема относится к представлению суммируемой функции в точках непрерывности, но суммируемая функция, вообще говоря, не имеет ни одной точки непрерывности, что понижает интерес этой теоремы.
Больший интерес представляет вопрос о представлении суммируемой функции в тех точках, где эта функция служит производной своего неопределенного интеграла, или в точках Лебега, так как и те и другие точки заполняют почти весь сегмент задания функции. Перейдем к рассмотрению этого вопроса.
Лемма (И. П. Натансон). Пусть на сегменте [ a , b ] дана суммируемая функция f (t), обладающая тем свойством, что
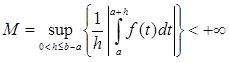 . (1)
. (1)
Какова бы ни была неотрицательная убывающая функция g(t), заданная и суммируемая на [ a , b ], интеграл
 (2)
(2)
существует (может быть как несобственный при t = a ) и справедливо неравенство
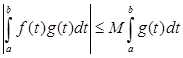 . (3)
. (3)
В пояснение условий леммы заметим, что не исключается случай, когда 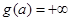 . Если же
. Если же 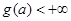 , то функция g(t) ограничена, и интеграл (2) существует как обычный интеграл Лебега.
, то функция g(t) ограничена, и интеграл (2) существует как обычный интеграл Лебега.
Переходя к доказательству леммы, заметим, что не ограничивая общности, можно принять, что g(b)=0. Действительно, если бы это не было так, то можно было ввести вместо g(t) функцию g *(t), определив ее равенствами
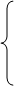 g(t), если
g(t), если 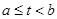 ,
,
g *(t)=
0, если t=b.
Доказав теорему для g *(t), мы затем смогли бы всюду заменить g *(t) на g(t), т. к. такая замена не отражается на величине интересующих нас интегралов. Итак, считаем, что g(b)=0.
Пусть a < α < b. На сегменте [ α, b ] функция g(t) ограничена, и интеграл
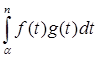 (4)
(4)
заведомо существует. Если положить 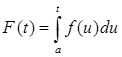 , то интеграл (4) можно записать в форме интеграла Стилтьеса
, то интеграл (4) можно записать в форме интеграла Стилтьеса
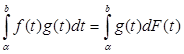 ,
,
откуда, после интегрирования по частям, находим
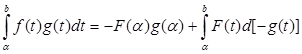 .
.
Но, в силу (1), мы имеем, что для любого h из интервала [0, t-a ] выполняется неравенство 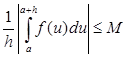 и следовательно
и следовательно
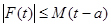 , (5)
, (5)
а так как g(t) убывает, то
 . (6)
. (6)
Значит 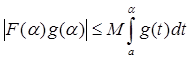 . С другой стороны, функция – g ( t ) возрастает. Отсюда и из (5) следует, что
. С другой стороны, функция – g ( t ) возрастает. Отсюда и из (5) следует, что
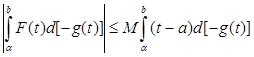 .
.
Преобразуем стоящий справа интеграл по формуле интегрирования по частям:
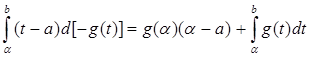 .
.
Отсюда, учитывая (6), следует, что
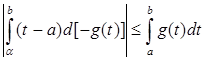 .
.
Сопоставляя все сказанное, получаем:
 . (7)
. (7)
Хотя это неравенство установлено при предположении, что g(b)=0, но оно останется верным и без этого предположения. Значит, можно заменить здесь предел b на β, где α< β < b. Но тогда, устремляя α и β к a, получим 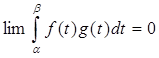 ,
,
чем доказывается существование интеграла (2). Если в (7) перейти к пределу при 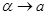 , то получим (3). Лемма доказана. (В оценке (3) множителя M уменьшить нельзя, так как при f (t)=1 в (3) достигается равенство.)
, то получим (3). Лемма доказана. (В оценке (3) множителя M уменьшить нельзя, так как при f (t)=1 в (3) достигается равенство.)
Теорема 2 (П. И. Романовский). Пусть ядро 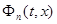 положительно и обладает следующим свойством: при фиксированных n и x ядро
положительно и обладает следующим свойством: при фиксированных n и x ядро 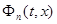 , как функция одного лишь t , возрастает в сегменте [ a , x ] и убывает в сегменте
, как функция одного лишь t , возрастает в сегменте [ a , x ] и убывает в сегменте
[ x , b ].
Тогда для любой суммируемой функции f (t), которая в точке x является производной своего неопределенного интеграла, будет 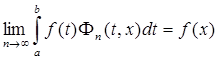 .
.
Доказательство. Так как 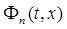 есть ядро, то
есть ядро, то 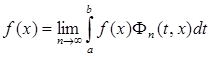 и достаточно проверить, что
и достаточно проверить, что 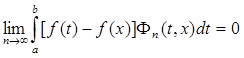 .
.
Разбивая последний интеграл на два, распространенные на сегменте
[ a , x ] и [ x , b ], рассмотрим второй из них, так как первый изучается аналогично.
Возьмем ε>0 и найдем такое δ>0, что при 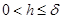 будет
будет
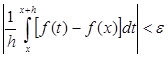 ,
,
что возможно, так как f (t) в точке t = x есть производная своего неопределенного интеграла. То есть 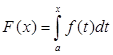 и
и  .
.
Тогда по предыдущей лемме
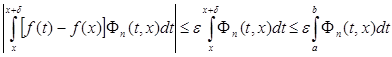 .
.
Так как 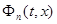 есть ядро, то
есть ядро, то 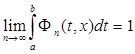 .
.
Величина, имеющая конечный предел, ограничена. Значит, существует постоянная K(x) такая, что  .
.
Таким образом,
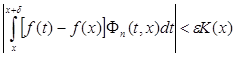 .
.
С другой стороны, если 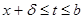 , то
, то
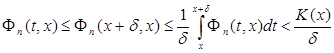 .
.
Значит функции 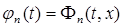 на сегменте [ x + δ , b ] равномерно ограничены и выполнено условие (5) теоремы Лебега из §1. Но второе ее условие, т. е. условие (6), также выполнено для этих функций, т. к.
на сегменте [ x + δ , b ] равномерно ограничены и выполнено условие (5) теоремы Лебега из §1. Но второе ее условие, т. е. условие (6), также выполнено для этих функций, т. к. 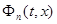 является ядром. Следовательно
является ядром. Следовательно 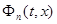 на сегменте [ x + δ , b ] слабо сходится к нулю, и для достаточно больших n будет
на сегменте [ x + δ , b ] слабо сходится к нулю, и для достаточно больших n будет 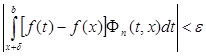 .
.
При этих n окажется
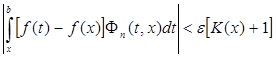 ,
,
так что
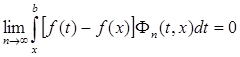 .
.
Теорема доказана.
В качестве примера ее приложения рассмотрим интеграл Вейерштрасса 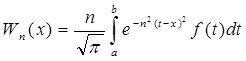 .
.
Функция 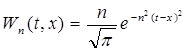 есть ядро, т. к. при α<x<β
есть ядро, т. к. при α<x<β
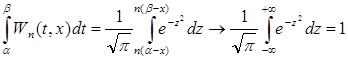 .
.
Эта функция положительна, и она возрастает при  и убывает при
и убывает при 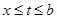 . Значит, для всякой
. Значит, для всякой 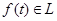 будет
будет 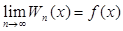 в каждой точке x, где f (t) есть производная своего неопределенного интеграла.
в каждой точке x, где f (t) есть производная своего неопределенного интеграла.
Определение. Функция Ψ( t , x ) называется горбатой мажорантой функции 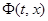 , если
, если 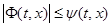 и если Ψ( t , x ) при фиксированном x возрастает на сегменте [ a , x ] и убывает на сегменте [ x , b ].
и если Ψ( t , x ) при фиксированном x возрастает на сегменте [ a , x ] и убывает на сегменте [ x , b ].
Теорема 3 (Д. К. Фаддеев). Если ядро 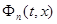 при каждом n имеет такую горбатую мажоранту
при каждом n имеет такую горбатую мажоранту 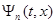 , что
, что
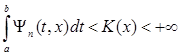 ,
,
где K(x) зависит лишь от x , то для любой 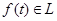 , имеющей точку t = x точкой Лебега, будет справедливо равенство
, имеющей точку t = x точкой Лебега, будет справедливо равенство
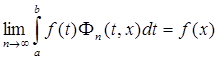 .
.
Доказательство. Достаточно доказать, что
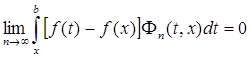 .
.
Возьмем ε>0 и найдем такое δ>0, что при 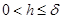 будет
будет
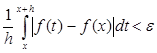 .
.
По лемме имеем
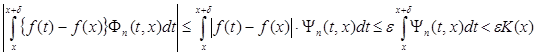 .
.
С другой стороны, в сегменте [ x + δ , b ] последовательность 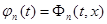 слабо сходится к нулю, т. к. при
слабо сходится к нулю, т. к. при 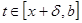 будет
будет
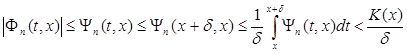 .
.
Следовательно для достаточно больших n будет
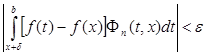 .
.
При этих n окажется 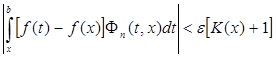 ,
,
так что 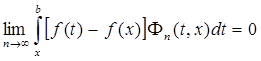 . Теорема доказана.
. Теорема доказана.
|
из
5.00
|
Обсуждение в статье: Представление функции сингулярным интегралом в заданной точке |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

