 |
Главная |
Приложения в теории рядов Фурье
|
из
5.00
|
Во введении мы уже определили понятие ряда Фурье функции f (x) по любой ортонормальной системе 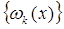 . В частности, если речь идет о тригонометрической системе
. В частности, если речь идет о тригонометрической системе
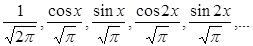 , (1)
, (1)
то рядом Фурье функции f (x) служит ряд
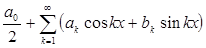 , (2)
, (2)
где
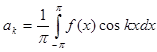 ,
, 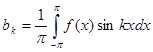 . (3)
. (3)
Во введении предполагали, что 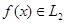 . Это предположение обеспечило существование коэффициентов Фурье
. Это предположение обеспечило существование коэффициентов Фурье 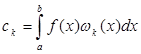 функции f (x) в любой ортонормальной системе. Но функции системы (1) ограничены. Поэтому коэффициенты (3), а с ними и ряд (2), можно образовать для любой суммируемой функции.
функции f (x) в любой ортонормальной системе. Но функции системы (1) ограничены. Поэтому коэффициенты (3), а с ними и ряд (2), можно образовать для любой суммируемой функции.
Вопрос о сходимости ряда (2) приводится к исследованию некоторого сингулярного интеграла. Если 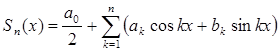 , то, в силу (3),
, то, в силу (3), 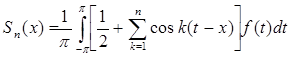 .
.
Выведем формулу для упрощения выражения в скобках. Для этого сложим равенства
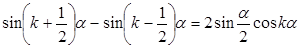 (k=0, 1, …, n-1),
(k=0, 1, …, n-1),
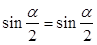 .
.
Это дает 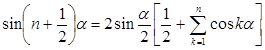 , откуда следует равенство
, откуда следует равенство
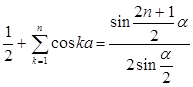 , (4)
, (4)
Пользуясь этой формулой, придадим сумме 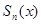 вид
вид
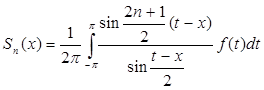 . (5)
. (5)
Этот интеграл есть сингулярный интеграл Дирихле.
Рассмотрим вопрос о суммировании ряда (2) по способу Чезаро. Этот способ состоит в отыскании предела среднего арифметического первых n сумм 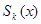 :
:

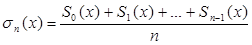 . (6)
. (6)
В случае сходимости ряда (2) в точке x последовательность 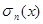 сходится к сумме ряда, но эта последовательность может сходиться и тогда, когда ряд (2) расходится.
сходится к сумме ряда, но эта последовательность может сходиться и тогда, когда ряд (2) расходится.
Для исследования 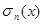 преобразуем ее с помощью формулы (5)
преобразуем ее с помощью формулы (5)
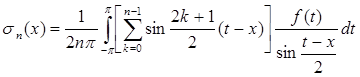 .
.
Но 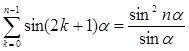 . (7)
. (7)
Действительно, складывая равенства
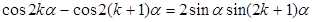 (k=0, 1, …, n-1),
(k=0, 1, …, n-1),
находим 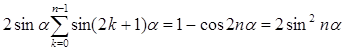 , откуда и следует (7).
, откуда и следует (7).
С помощью (7) получаем 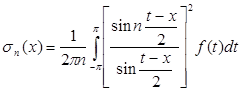 . (8)
. (8)
Интеграл (8) есть сингулярный интеграл Фейера. Покажем, что для него выполнены условия теоремы Фаддеева.
Для этого рассмотрим функцию f (t)=1. Вычисляя ее коэффициенты Фурье по формулам (3), получим 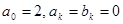 (k=1, 2, …).
(k=1, 2, …).
Значит, для этой функции 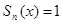 (n=0, 1, 2, …), а следовательно и
(n=0, 1, 2, …), а следовательно и 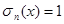 .
.
Но выражая 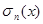 интегралом Фейера, получим, что
интегралом Фейера, получим, что
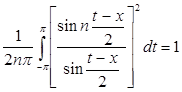 . (9)
. (9)
Заметив это, рассмотрим точку 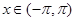 . Пусть
. Пусть 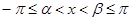 . Если
. Если 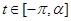 , то
, то 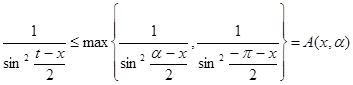 , и, следовательно,
, и, следовательно, 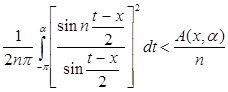 , где A ( x , α ) не зависит от n.
, где A ( x , α ) не зависит от n.
Отсюда следует, что 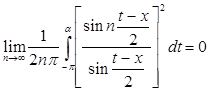 .
.
Аналогично убедимся, что интеграл стремится к нулю по промежутку [β, π]. Сопоставляя это с (9), находим, что
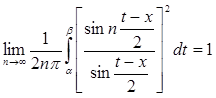 ,
,
так что функция 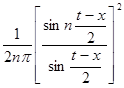 есть ядро.
есть ядро.
Для этого ядра можно построить горбатую мажоранту. Заметим, что 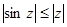 . Отсюда
. Отсюда 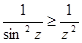 . Но
. Но 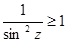 .
.
Следовательно 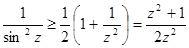 и
и
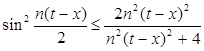 . (10)
. (10)
С другой стороны, когда 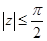 , то
, то 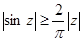 , так что
, так что
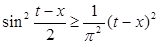 . (11)
. (11)
Так как 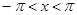 ,
, 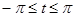 , то
, то 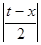 может оказаться и больше, чем
может оказаться и больше, чем 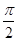 . Но это несущественно. Если положим
. Но это несущественно. Если положим 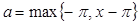 ,
, 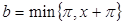 , то разность между интегралом Фейера (8) и интегралом
, то разность между интегралом Фейера (8) и интегралом
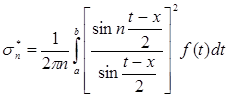
при возрастании n стремится к нулю (т. к., например, при 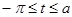 будет
будет 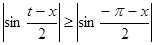 ), поэтому все рассуждения можно вести для интеграла
), поэтому все рассуждения можно вести для интеграла 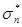 .
.
Из (10) и (11) следует, что
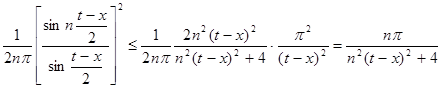 .
.
Функция 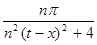 есть горбатая мажоранта ядра Фейера.
есть горбатая мажоранта ядра Фейера.
Но 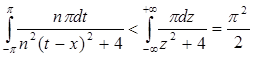 , т. е. интегралы от мажоранты ограничены числом, не зависящим от n.
, т. е. интегралы от мажоранты ограничены числом, не зависящим от n.
Итак, интеграл Фейера удовлетворяет условиям теоремы
Д. К. Фаддеева. Отсюда следует
Теорема 1 (Л. Фейер – А. Лебег). Почти везде на [- π , + π ] будет
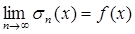 . (12)
. (12)
Это соотношение выполняется во всех точках Лебега и тем более во всех точках непрерывности функции f (t), лежащих внутри [- π , + π ].
Тригонометрическая система полна. Это означает, что всякая функция 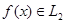 , у которой все коэффициенты Фурье (3) равны нулю, эквивалентна нулю. Избавимся от ограничения, что f (x) суммируема с квадратом. Справедлива следующая
, у которой все коэффициенты Фурье (3) равны нулю, эквивалентна нулю. Избавимся от ограничения, что f (x) суммируема с квадратом. Справедлива следующая
Теорема 2. Если все коэффициенты Фурье (3) суммируемой функции
f (x) равны нулю, то f (x) эквивалентна нулю.
В самом деле, в этом случае 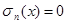 и, следовательно, f (x)=0 во всех точках, где имеет место (12), т. е. почти везде.
и, следовательно, f (x)=0 во всех точках, где имеет место (12), т. е. почти везде.
Теорема 1 позволяет делать некоторые высказывания и о поведении сумм 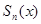 . Для этого заметим, что
. Для этого заметим, что
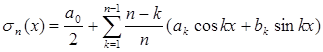 ,
,
так что 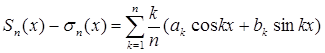 .
.
Отсюда 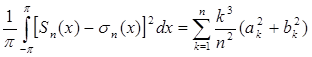 .
.
|
из
5.00
|
Обсуждение в статье: Приложения в теории рядов Фурье |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

