 |
Главная |
Подведение итогов занятия:
|
из
5.00
|
- Интересными ли явились задания?
- Не являются ли они сложными или, наоборот, простыми?
Выставление учениками самим себе баллов за каждое верно решенное задание (1 задание – 1 балл).
Постановка домашнего задания:
Задания, аналогичные задачам, решаемым на занятии:
№1. а) При каких значениях k оба корня уравнения х2+(16- k )х+ k +8=0 равны 0?
б) При каких значениях а корни уравнения х2-2х+ m -1=0
равны по модулю, но противоположны по знаку?
№2. При каких а уравнение
а) (а  -4)х
-4)х  +(2а-4)х-(а-2)=0 имеет не менее одного решения;
+(2а-4)х-(а-2)=0 имеет не менее одного решения;
б) (а+1)х  +2(а+1)х-2=0 не имеет корней.
+2(а+1)х-2=0 не имеет корней.
Задания на самостоятельный поиск решения:
№3. а) Найти корни квадратного уравнения ах2+ b х+с=0, если а– b +с=0.
б) При каких значениях параметра а уравнения 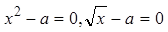 равносильны? (Вспомнить, какие уравнения называются равносильными)
равносильны? (Вспомнить, какие уравнения называются равносильными)
Литература: [3], [8], [12], [13], [18].
Занятие II . Теорема Виета. Знаки корней квадратного трехчлена
Цель: формирование умения определять знаки корней квадратного трехчлена, применяя теорему Виета.
Ход занятия:
1. Организационный момент. Сообщение темы и целей занятия.
2. Проверка домашнего задания: решение №1, №2 записано учителем на доске, ученики проверяют; №3: один из учеников, выполнивший задание №3а), записывает до начала занятия решение на доске, второй - №3б); затем задания разбираются. Если задания никем не выполнены, то решение объясняет учитель.
Обзорная лекция по теме «Теорема Виета. Знаки корней квадратного уравнения».
Теорема Виета: Если дискриминант  (при А
(при А  0), то трехчлен Ax
0), то трехчлен Ax  + B х+ C имеет корни
+ B х+ C имеет корни  и
и 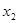 , удовлетворяющие соотношениям:
, удовлетворяющие соотношениям: 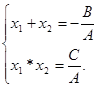 (*)
(*)
И наоборот, если числа  и
и 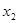 удовлетворяют соотношениям(*), то они являются корнями квадратного трехчлена Ax
удовлетворяют соотношениям(*), то они являются корнями квадратного трехчлена Ax 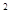 + B х+ C.
+ B х+ C.
Исходя из теоремы Виета, получаются условия, определяющие знак корней трехчлена (Таблица 3).
Таблица 3.
| Знак корней |  >0 >0
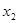 >0 >0
|   0 0
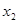  0 0
|  <0 <0
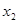 <0 <0
|   0 0
  0 0
|  >0 >0
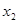 <0 <0
|  =0 =0
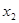 >0 >0
|  =0 =0
 <0 <0
|
| Условия | 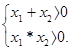
| 
| 
| 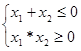
| 
| 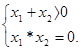
| 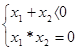
|
4. Решение задач. Задание 1 решает один из учеников на доске. Затем ученики выполняют задания самостоятельно с последующей проверкой на доске.
Задания:
1. При каком значении параметра а уравнение х2+(3а-5)х-2=0 имеет корни разных знаков?
2. При каком значении параметра а корни трехчлена (а  -4)х2+(а+2)х+2 положительны?
-4)х2+(а+2)х+2 положительны?
3. Найти все а, для которых уравнение (а-1)х2+(2а+3)х+2+а=0 имеет корни одного знака.
4. Найти все а, при которых неравенство  справедливо для всех неотрицательных х.
справедливо для всех неотрицательных х.
5. Не решая уравнение определить знаки его корней: ах  +2(а+1)х+2а=0;
+2(а+1)х+2а=0;
Дополнительные задания:
6. При каких значениях р неравенство 5х  -4(р+3)х+4<р
-4(р+3)х+4<р  справедливо для всех отрицательных х?
справедливо для всех отрицательных х?
7. Определить знак корней уравнения:
а) 3ах  +(4-6а)+3(а-1)=0; б) (а-3)х2-2(3а-4)х+7а-6=0.
+(4-6а)+3(а-1)=0; б) (а-3)х2-2(3а-4)х+7а-6=0.
8. Решить уравнение, используя теорему Виета: х2-(2а+1)х+а+а2=0.
Подведение итогов.
- Какова была тема занятия? Что нового узнали на занятии?
- Достигли ли цели, поставленной в начале занятия?
Учитель ставит баллы (от 1 до 8) ученикам, наиболее активно работавшим на занятии.
|
из
5.00
|
Обсуждение в статье: Подведение итогов занятия: |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

