Доверительный интервал

Доверительным называют интервал ( , где k= n-1 степеней свободы, s*— исправленное среднее квадратическое отклонение, — надежность оценки

Доверительный интервал для X.

Доверительный интервал для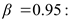

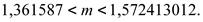
Доверительный интервал для

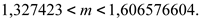
Доверительный интервал для

Доверительный интервал для Y рассчитывается аналогично.

Проверка гипотез

Статистической называют гипотезу о виде неизвестного распределений или о параметрах известных распределений. Нулевой называют выдвинутую гипотезу Н₀. Конкурирующей гипотезой называют гипотезу Н₁, которая противоречит нулевой. Простой называют гипотезу, содержащую только одно предположение. Сложной называет гипотезу, которая состоит из конечного или бесконечного числа простых гипотез. Статистическим критерием называют величину К, которая служит для проверки гипотезы. Наблюдаемым (эмпирическим) значением критерия К_набл называют то значение критерия, которое вычислено по выборкам. Критической областью называют совокупность значений, при которых нулевую гипотезу отвергают. Областью принятия гипотезы называют совокупность значений, при которых нулевую гипотезу принимают. Основной принцип проверки статистических гипотез: если К_набл принадлежит критической области, то нулевую гипотезу отвергают; если наблюдаемое значение критерия принадлежит области принятия гипотезы, то гипотезу принимают. Критическими точками k_кр называют точки, отделяющие критическую область от области принятия гипотезы. Правосторонней называют критическую область, определяемую неравенством К > k_кр , где k_кр — положительное число. Левосторонней называю критическую область, определяемую неравенством К < k_кр , где k_кр — отрицательное число. Двухсторонней называют критическую область, определяемую неравенствами K<k₁, K>k₂, k₂>k₁.

Для отыскания критической области задаются уровнем значимости α и ищут критические точки, исходя из следующих соотношений:

1. для правосторонней критической области

P(K>k_кр) = α (k_кр>0);

2. для левосторонней критической области

P(K<k_кр) = α (k_кр<0);

3. для двухсторонней симметричной области

P(K>k_кр) = α/2 (k_кр>0), P(K<-k_кр) = α/2.

Сравнение выборочной средней с гипотетической генеральной средней (Дисперсия генеральной совокупности неизвестна).

Если дисперсия генеральной совокупности неизвестна, то в качестве критерия проверки нулевой гипотезы принимают случайную величину

где — исправленное среднее квадратическое отклонение. Величина T имеет распределение Стьюдента с k = n-1 степенями свободы.

Правило 1. Для того, чтобы при заданном уровне значимости α проверить нулевую гипотезу H₀: а=а₀ о равенстве неизвестной генеральной средней а гипотетическому значению а₀ при конкурирующей гипотезе H₁: а≠а₀, надо вычислить наблюдаемое значение критерия

и по таблице критических точек распределения Стьюдента по заданному уровню значимости α и числу степеней свободы k = n-1 найти критическую точку t_{двуст. кр}(α; k).

Если 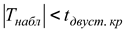— нет оснований отвергнуть нулевую гипотезу. Если — нулевую гипотезу отвергают.

Правило 2. При конкурирующей гипотезе H₁: а>а₀, по уровню значимости α, помещенному в нижней строке таблицы приложения 6 пункта 1 из списка литературы, и числу степеней свободы k=n-1 находят критическую точку t_{правост. к}.(α; k) правосторонней критической области.Если — нет оснований отвергнуть нулевую гипотезу. Если — нулевую гипотезу отвергают.

Правило 3. При конкурирующей гипотезе H₁: а<а₀ сначала находят «вспомогательную» критическую точку (по правилу 2) t_{правост. к}.(α; k) и полагают границу левосторонней критической области t_{левост. кр.}=– t_{правост. кр.}. Если , нет оснований отвергнуть нулевую гипотезу. Если — нулевую гипотезу отвергают.

Для данной работы:

S= 0,526002;

1,467

α=0,05

a₀=1,5

k=99

T=-0,627373528

Правило 1.

а=1,5

 

t_{двуст. кр}(α; k)= t_{двуст.кр}(0,05;99)=1,99

— нет оснований отвергнуть нулевую гипотезу, т. е выборочная средняя 1,467 незначительно отличается от гипотетической генеральной средней a₀=1,5.

Правило 2.

a>1,5

t_{правост. кр.} (α; k)= t_{правост. кр.} (0,05; 99)=1,661

— нет оснований отвергнуть нулевую гипотезу.

Правило 3.

a<1,5

t_{правост. кр.} (α; k)= t_{правост. кр.} (0,05; 99)=1,661

t_{левост. кр.}=– t_{правост. кр.}= – 1,661

— нет оснований отвергнуть нулевую гипотезу.

Все параметры по Y находятся аналогично.

Проверка гипотезы о нормальном распределении генеральной совокупности по критерию Пирсона

Пусть эмпирическое распределение задано в виде последовательных интервалов (x_i, x_i+1) и соответствующим им частот n_i. Требуется, используя критерий Пирсона проверить гипотезу о том, что генеральная совокупность Xраспределена нормально.

Правило: Чтобы при уровне значимости α проверить гипотезу о нормальном распределении генеральной совокупности, надо:

1. Вычислить выборочную среднюю и выборочное среднее квадратическое отклонение , причем .

2. Перейти к случайной величине , и вычислить концы интервалов , .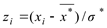

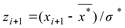3. Вычислить теоретические частоты , где n — объем выборки; Р_i=Ф(z_i+1)– Ф(z_i) — вероятности попадания X в интервалы (x_i, x_i+1); Ф(Z) — функция Лапласа.

4. Сравнить эмпирические и теоретические частоты с помощью критерия Пирсона. Для этого строят таблицу и находят значение критерия Пирсона . По таблице распределения

 

Вывод

Проведя обработку выборочной совокупности случайно отобранных статистических данных, мы получили некоторые оценки их параметров, а также выяснили, что данная выборка случайных величин имеет такую зависимость, что при росте значения X увеличивается и значение Y, т.е., переводя на тему курсовой работы. При увеличении радиации число лейкоцитов возрастает. Зависимость параболическая, поэтому Уравнение зависимости Y от X выглядит следующим образом:

y =–69,58x²+6266,7x+954,82

 

Список литературы

1. Гмурман В. Е. Руководство к решению задач по теории вероятностей и математической статистике. — М.: Высшая школа, 1998.

2. Гмурман В. Е. Теория вероятностей и математическая статистика. — М.: Высшая школа, 1977.

3. Чавлейшвили М. П. Курс лекций

4. Кабанова Е. И Теория вероятностей и математическая статистика. Курс лекций.—Дубна, 1996.

5. Мазный Г. Л., Прогулова Т. Б. Методическое пособие к курсовому проектированию по высшей математике. - Дубна, 1996.

6. Радиация, ее влияние на организм человека. http://monax.ru/order/

7. Большая Советская Энциклопедия. Т.14. — М., 1973

 

Приложение

Рис 1. Диаграмма рассеивания

Рис 2 . Гистограмма рассеивания относительных частот для X

Рис. 3. Гистограмма рассеивания относительных частот для Y

 

Рис.4 Полигон относительных частот для X

Рис.5 Полигон относительных частот для Y

 

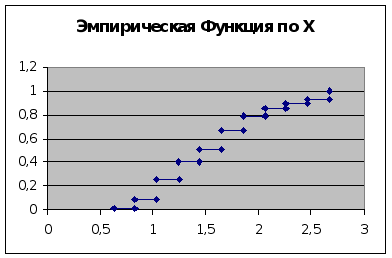
Рис6 Эмпирическая функция распределения Х

Рис.7 Эмпирическая функция распределения Y

 

Рис. 8. График линейной регрессии

 

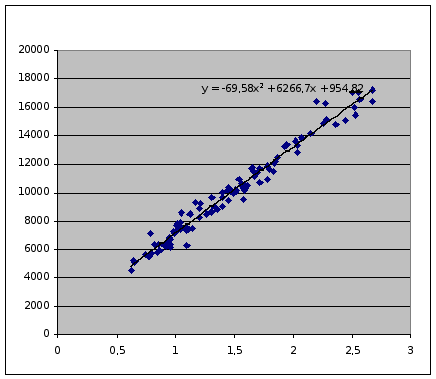
Рис. 9. График параболической регрессии

 

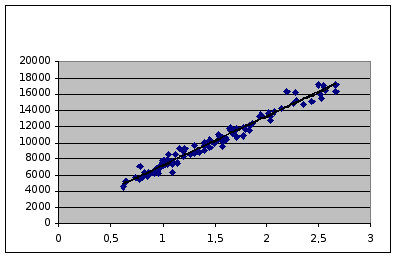
Рис.10. Сравнение линейной и параболической регрессий

Дата

ФИО

Подпись