 |
Главная |
Испытания по схеме Бернулли.
|
из
5.00
|
Так называется следующая серия независимых испытаний. Пусть производится n испытаний. В i-том испытании может осуществиться случайное событие Ai с вероятностью Рi,i=1,…,n. Все события А i независимы в совокупности. То есть вероятность события А i не зависит от того, осуществляются или нет события А j,j=1,…,n, j 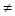 i. Рассмотрим здесь такой частный случай, когда все вероятности Рi равны друг другу и равны p,0‹p‹1. То есть
i. Рассмотрим здесь такой частный случай, когда все вероятности Рi равны друг другу и равны p,0‹p‹1. То есть
Р(А i )=p , P(Ai*)=q, q=1-p, 0‹p‹1, 0‹q‹1, i=1,…,n (13.1)
Например, пусть испытания состоят в том, что случайная точка 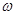 в i-том испытании обязательно появляется в квадрате со стороной равной единице. Событие А i состоит в том, что точка
в i-том испытании обязательно появляется в квадрате со стороной равной единице. Событие А i состоит в том, что точка 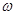 оказывается в четверти круга, вписанного в квадрат и имеющего радиус равный единице (см.раздел7). Согласно (7.2) имеем
оказывается в четверти круга, вписанного в квадрат и имеющего радиус равный единице (см.раздел7). Согласно (7.2) имеем
Р( Ai )=p= 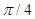 (13.2)
(13.2)
Справедливо следующее утверждение.
Теорема Бернулли: Пусть производится n испытаний по схеме Бернулли. Пусть события А i осуществились в m испытаниях.
Для любых чисел 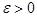 и
и 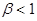 найдется такое натуральное число N , что при числе испытаний n>N будетсправедливо неравенство
найдется такое натуральное число N , что при числе испытаний n>N будетсправедливо неравенство
P(|m/n–p|< 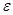 )>
)> 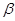 (13.3)
(13.3)
В самом деле, свяжем с i-тым испытанием случайную величину 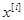 . Пусть эта величина принимает значение равное единице, если осуществляется событие А i , и
. Пусть эта величина принимает значение равное единице, если осуществляется событие А i , и 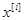 принимает значение равное нулю, если событие А i не осуществляется, т.е. осуществляется противоположное событие А i *. Вычислим математическое ожидание Е i и дисперсию Di случайной величины
принимает значение равное нулю, если событие А i не осуществляется, т.е. осуществляется противоположное событие А i *. Вычислим математическое ожидание Е i и дисперсию Di случайной величины 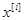 . Имеем
. Имеем
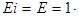 p
p 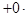 q=p (13.4)
q=p (13.4)
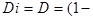 p
p 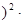 p
p 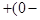 p
p 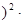 q
q 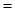 q
q  ∙p+p
∙p+p  ∙q=p∙q∙(q+p)=p∙q∙1=p∙q (13.5)
∙q=p∙q∙(q+p)=p∙q∙1=p∙q (13.5)
Так как в нашем случае
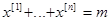 (13.6)
(13.6)
то из закона больших чисел (12.9),(12.10) получаем неравенство (13.3), если только
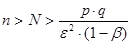 (13.7)
(13.7)
Это и доказывает теорему Бернулли.
Например, если мы хотим проверить теорему Бернулли на примере вычисления числа π с точностью до 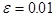 с вероятностью большей, чем
с вероятностью большей, чем 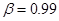 , то нам надо сделать испытания по схеме Бернулли в соответствии с разделом 7, т.е. получить согласно текущему разделу неравенство
, то нам надо сделать испытания по схеме Бернулли в соответствии с разделом 7, т.е. получить согласно текущему разделу неравенство
P(|m/n– π/4|<0.01)>0.99 (13.8)
Для этого согласно (13.7) достаточно выбрать число
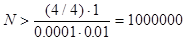 (13.9)
(13.9)
с большим запасом.
Такое испытание было сделано на компьютере по программе, приведенной в следующем разделе. Получилось
4∙m/n=3.1424 (13.10)
Мы знаем, что число π=3.1415925626…. То есть действительно получилось число с точностью по крайней мере до 0.01.
14.Программа вычисления числа π по схеме Бернулли.
CLS
INPUT "Введите n=", n
RANDOMIZE
FOR i = 1 TO n
x = RND
y = RND
IF (x * x + y * y) < 1 THEN m = m + 1 ELSE m = m
NEXT i
pi = 4 * m / n
PRINT "pi = ", pi
Метод Монте-Карло.
Испытания по схеме Бернулли составляют основу вычислительного метода, который предложил Фон-Нейман для расчета сложных процессов. Например, для расчетов при создании атомной бомбы. Этот метод он назвал методом Монте-Карло в честь города, в котором идет игра в рулетку. Суть этого метода состоит в том, что подбираются такие испытания по схеме Бернулли, в которых вероятности событий А i и определяют интересующую вычислителя величину. Простейший пример вычисления по методу Монте-Карло и приведен в разделах 13,14 для числа π. Особенно удобно вычислять методом Монте-Карло площади и объемы сложных фигур и тел.
Стрельба по вепрю.
Задача 16.1.:
Три охотника стреляют по вепрю. Известно, что первый охотник попадает в цель с вероятностью 0.7. Второй – с вероятностью 0.5. Третий – с вероятностью 0.3. Результат стрельбы каждого из них не зависит от результатов стрельбы других. Все три охотника дали один залп.
Какова вероятность, что в вепря попали 2 пули?
Решение:
Назовем попадание первого охотника событием А1, попадание второго – А2, попадание третьего – А3.
Для того, чтобы попали две пули необходимо и достаточно, чтобы осуществилось одно и только одно из следующих трех несовместных событий:
В1-первый попал, второй попал, третий промазал, В1=А1  А2
А2  А3*
А3*
В2-первый попал, второй промазал, третий попал, В2=А1  А2*
А2*  А3
А3
В3-первый промазал, второй попал, третий попал, В3=А1*  А2
А2  А3
А3
Так как события попадания для разных стрелков независимы, то вероятности попадания равны произведению вероятностей. Поэтому
Р(В1)=Р(А1)∙Р(А2)∙Р(А3*)=0.7∙0.5∙0.7=0.245
Р(В2)=Р(А1)∙Р(А2*)∙Р(А3)=0.7∙0.5∙0.3=0.105
Р(В3)=Р(А1*)∙Р(А2)∙Р(А3)=0.3∙0.5∙0.7=0.105
Интересующее нас событие С=В1 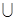 В2
В2 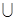 В3. Так как события В1,В2 и В3 несовместны, то вероятность объединения равна сумме вероятностей событий В i,i=1,2,3
В3. Так как события В1,В2 и В3 несовместны, то вероятность объединения равна сумме вероятностей событий В i,i=1,2,3
Р(С)=Р(В1)+Р(В2)+Р(В3)=0.245+0.105+0.105=0.455 (16.1)
Ответ: Вероятность, что попали 2 пули равна 0.455.
Задача 16.2.:
Те же охотники дали залп по другому вепрю. Известно, что попали 2 пули.
Какова вероятность, что попал первый охотник?
Решение:
Интересующая нас вероятность есть условная вероятность Р(А1 | С) события А1 при условии, что произошло событие С. По формуле Бейеса имеем
Р(А1 |C )=P(C|A1)∙P(A1)/P(C) (16.2)
По определению условной вероятности P(C|A1) (3.1) и (3.2) имеем
P(C|A1)∙P(A1)=Р(С  А1) (16.3)
А1) (16.3)
Но событие С  А1 происходит тогда и только тогда, когда происходит одно из двух несовместимых событий
А1 происходит тогда и только тогда, когда происходит одно из двух несовместимых событий
С2=А2  А3*
А3*  А1 (16.4)
А1 (16.4)
С3=А3  А2*
А2*  А1 (16.5)
А1 (16.5)
То есть имеем
(С  А1) =(А2
А1) =(А2  А3*
А3*  А1)
А1) 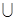 (А3
(А3  А2*
А2*  А1) (16.6)
А1) (16.6)
Р(С  А1) =Р(А2
А1) =Р(А2  А3*
А3*  А1)+Р(А3
А1)+Р(А3  А2*
А2*  А1)=0.5∙0.7∙0.7+0.3∙0.5∙0.7=
А1)=0.5∙0.7∙0.7+0.3∙0.5∙0.7=
=0.245+0.105=0.35 (16.7)
Таким образом, согласно (16.2) для искомой условной вероятности Р( A1|C ) получим значение
Р( A1|C )=P(C|A1)∙P(A1)/P(C)=0.35/0.455=0.769 (16.8)
Ответ: Вероятность того, что попал первый охотник при условии, что попало в вепря две пули равна 0.769.
|
из
5.00
|
Обсуждение в статье: Испытания по схеме Бернулли. |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

