Пузырьковая сортировка с просеиванием

Сортировка

Сортировка является наиболее фундаментальной алгоритмической задачей в теории вычислительных машин и систем по двум различным причинам. Во-первых, сортировка – это полезная операция, которая эффективно решает многие задачи, с которыми встречается каждый программист. Во-вторых, были разработаны буквально десятки различных алгоритмов сортировки, каждый из которых основывается на определенной хитрой идее или наблюдении. Большинство примеров разработки алгоритмов ведет к интересным алгоритмам, включающим «разделяй и властвуй», рандомизацию, инкрементную вставку и продвинутые структуры данных. Из свойств этих алгоритмов следует множество интересных задач по программированию.

Ключом к пониманию сортировки является понимание того, как она может быть использована для решения многих важных задач программирования. Рассмотрим некоторые случаи применения сортировки.

· Проверка уникальности. Как мы можем проверить, все ли элементы данного набора объектов S являются различными? Отсортируем их либо в возрастающем, либо в убывающем порядке, так что любые повторяющиеся объекты будут следовать друг за другом. После этого один проход по всем элементам с проверкой равенства S[i]=s[i+1] для любого 1≤i<n решает поставленную задачу.

· Удаление повторяющихся элементов. Как мы можем удалить все копии, кроме одной, любого из повторяющихся элементов S? Сортировка и чистка снова решают задачу. Обратите внимание, что чистку проще всего производить, использую два индекса – back, указывающий на последний элемент в очищенной части массива, и i, указывающий на следующий элемент, который нужно рассмотреть. Если S[back]<>S[i], увеличиваем back и копируем S[i] в S[back].

· Распределение приоритетов событий. Предположим, что у нас имеется список работ, которые необходимо сделать, и для каждой определен свой собственный срок сдачи. Сортировка объектов по времени сдачи (или по аналогичному критерию) расположит работы в том порядке, в котором их необходимо делать. Очереди по приоритетам удобны для работы с календарями и расписаниями, когда имеется операции вставки и удаления, но сортировка удобна в том случае, когда набор событий не меняется в ходе выполнения.

· Медиана/выбор. Предположим, что мы хотим найти k-й по величине объект в S. После сортировки объектов в порядке возрастания нужный нам будет находится в ячейке S[k]. В определенных случаях этот подход может быть использован для нахождения наименьшего, наибольшего и медианного объекта.

· Расчет частоты. Какой элемент чаще всего встречается в S? После сортировки линейный проход позволяет нам посчитать число раз, которое встречается каждый элемент.

· Восстановление первоначального порядка. Как мы можем восстановить первоначальное расположение набора объектов, после того как мы переставили их для некоторых целей? Добавим дополнительное поле к записи данных объекта, такое что i-й записи это поле равняется i. Сохранив это поле во время всех перестановок, мы сможем отсортировать по нему тогда, когда нам потребуется восстановить первоначальный порядок.

· Создание пересечения/объединения. Как мы можем рассчитать пересечение или объединение двух контейнеров? Если они оба отсортированы, мы может объединить их, если будем выбирать наименьший из двух ведущих элементов, помещать его в новое множество, если хотим, а затем удалять из соответствующего списка.

· Поиск необходимой пары. Как мы можем проверить, существуют ли два целых числа x,y S таких ,что x+y=z для какого-то заданного z? Вместо того, чтобы перебирать все возможные пары, отсортируем числа в порядке возрастания. С ростом S[i], при увеличении I, его возможный партнер j, такой что S[j]=z-S[i], уменьшается. Таким образом, уменьшая j соответствующим образом при увеличении I, мы получаем изящное решение.

· Эффективный поиск. Как мы можем эффективно проверить, принадлежит ли элемент s множеству S? Конечно, упорядочивание множества с целью применения эффективного бинарного поиска – это, наверное, наиболее стандартное приложение сортировки. Просто не забывайте остальные!

Рассмотрим несколько достаточно поучительных алгоритмов сортировки

Сортировка пузырьком

Расположим массив сверху вниз, от нулевого элемента - к последнему. Идея метода: шаг сортировки состоит в проходе снизу вверх по массиву. По пути просматриваются пары соседних элементов. Если элементы некоторой пары находятся в неправильном порядке, то меняем их местами.

После нулевого прохода по массиву "вверху" оказывается самый "легкий" элемент - отсюда аналогия с пузырьком. Следующий проход делается до второго сверху элемента, таким образом второй по величине элемент поднимается на правильную позицию... Делаем проходы по все уменьшающейся нижней части массива до тех пор, пока в ней не останется только один элемент. На этом сортировка заканчивается, так как последовательность упорядочена по возрастанию.

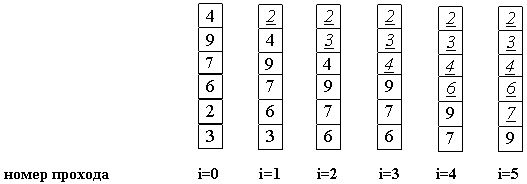
Type

arrType = Array[1 .. n] Of Integer;

Procedure Bubble(Var ar: arrType; n: integer);

Var i, j, T: Integer;

Begin

For i := 1 To n Do

For j := n DownTo i+1 Do

If ar[Pred(j)] > ar[j] Then Begin { < }

T := ar[Pred(j)]; ar[Pred(j)] := ar[j]; ar[j] := T

End

End;

Сложность этого метода сортировки составляет О(n^2)

Пузырьковая сортировка с просеиванием

Аналогичен методу пузырьковой сортировки, но после перестановки пары соседних элементов выполняется просеивание: наименьший левый элемент продвигается к началу массива насколько это возможно, пока не выполняется условие упорядоченности.

Преимущество: простой метод пузырька работает крайне медленно, когда мин/макс (в зависимости от направления сортировки) элемент массива стоит в конце, этот алгоритм - намного быстрее.

const n = 10;

var

x: array[1 .. n] of integer;

i, j, t: integer;

flagsort: boolean;

procedure bubble_P;

begin

repeat

flagsort:=true;

for i:=1 to n-1 do

if not(x[i]<=x[i+1]) then begin

   t:=x[i];

   x[i]:=x[i+1];

   x[i+1]:=t;

   j:=i;

   while (j>1)and not(x[j-1]<=x[j]) do begin
     t:=x[j];
     x[j]:=x[j-1];
     x[j-1]:=t;
     dec(j);
   end;
   flagsort:=false;
end;
until flagsort;
end;

Тестировалось на массиве целых чисел (25000 элементов).

Прирост скорости относительно простой пузырьковой сортировки - около 75%...